李老师专用教案（精品原创） 微信：15192086110抖音：866460001

101 数学加分宝9 上《天天练》第11 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1.若（ 1 x ， 1 y ）、（ 2 x ， 2 y ）、（ 3 x ， 3 y ）都是反比例函数

x

y

1   图象上的点，并且1 23y0yy，则下列各式中正确的是（ D ）21 世纪教育网版权所有 h A. 1 2 3 x  x  x B. 1 3 2 x  x  x C. 2 1 3 x  x  x D. 2 3 1 x x x2.在反比例函

x

m

y

1 3  数图象上有两点 A（ 1 x ， 1 y ）、B （ 2 x ， 2 y ），若1 2 x 0x，1 2yy，则m的取值范围是

3

1

m  .二.（每题 5 分，共 10 分）

1.在同一坐标系中，函数

x

k

y  和 y  kx  3的图象大致是（ A ）

A. B. C. D.

2.如图，关于 x 的函数 y=k（x−1）和 y=− k

x

（k≠0）， 它们在同一坐标系内的图象大致是（B）三.（每题 5 分，共 10 分）

1.如图，面积为 3 的矩形OABC 的一个顶点 B 在反比例函数

x

k

y  的图象上，另三点在坐标轴上，则k-3.2.如图，O 是坐标原点，菱形OABC 的顶点 A 的坐标为（-3，4），顶点C在x 轴的负半轴上，函数(x＜0)

x

k

y  的图象经过顶点 B ，则 k 的值为___-32 ___.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

102 数学加分宝9 上《天天练》第11 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.如图，点 M 是反比例函数

x

a

y  （ a  0 ）的图象上一点，过 M点作 x 轴、y 轴的平行线，若S阴影5，则此反比例函数关系式为

x

y

5   ．

2.（15年市南期末）如图，两个反比例函数

1

y

x  和

2

y

x   的图象分别是 1

l 和2

l ．设点P在1

l 上，PCx轴，垂足为C ，交 2

l 于点 A ， PD  y 轴，垂足为 D ，交 2

l 于点 B ，则 PAB的面积为29．二.（每题 5 分，共 10 分）

1.（18年市南期末）如图，平行于x轴的直线与函数 = ( > 0 > 0) 1

1 k x

x

k

y ，， = ( >0>0)2

2 k xx

k

y ，的图象分别相交于A，B两点，点A在点B的右侧，C为x轴上的一个动点.若∆ABC的面积为4，则k1−k2的值为（B）A.−8 B.8 C.4 D.−4

2.如图所示，是反比例函数

x

y

3  和

x

y

7 = －在 x 轴上方的图象，点C是 y 轴正半轴上的一点，过点C作AB // x 轴分别交这两个图象于点 A 和点 B ，若点 P 在 x 轴上运动，则 ABP的面积等于5 .

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

103 数学加分宝三.（每题 5 分，共 10 分）

1.如图，直线 x  t （t＞0 ）与反比例函数

x

y

2 = ， x

y

1 = －的图象分别交于B，C两点，A为y轴上的任意一点，则 ABC 的面积为 2

3

.

2.（14年市南期末）如图，已知双曲线

x

k

y  (k < 0) 经过 RtΔOAB 斜边OA的中点D，且与直角边AB相交于点C ，若 ΔCOD 的面积为6，则 k 的值为 −8 ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

104 数学加分宝9 上《天天练》第11 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1.使函数 2 9 19

2 (2 7 9)

    

m m y m m x 是反比例函数，且图象在每个象限内 y 随x 的增大而减小，则可列方程（不等式组）为





  

   

2 7 9 0

9 19 1

2

2

m m ＞m m

．

2.如图，点B在反比例函数

x

y

6  (x  0) 的图象上，点C在反比例函数

x

y

2  (x 0) 的图象上，且BC∥y轴，AC⊥BC，垂足为点C，交 y 轴于点A，则△ABC的面积为（ B ）

A.3 B.4 C.5 D.6

二.（每题 5 分，共 10 分）

1.（19年市北期末）已知函数

x

y  6  与 y  x 1的图象的交点坐标是（a，b），则ab11的值为61.2.已知函数 y  ax 和

x

a

y 



4 的图象有两个交点，其中一个交点的横坐标为1，则两个函数图象的交点坐标是__（1,2）（, 1,2）__；

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

105 数学加分宝三.（每题 5 分，共 10 分）

1.如图所示，在平面坐标系中， AB  x 轴，反比例函数

x

k

y

1  （ k1  0 ）过B点，反比例函数xky2（ 0 k2  ）过C 、 D 点，OC  BC ， B （2，3），则 D 点的坐标为（ D ）A.（

2

3 ， 9

5 ） B.（

3

5 ，

2

5 ） C.（

3

4 ， 4

5 ） D.（

3

10 ，210）2.如图，在反比例函数

x

y

2  （ x＞0 ）的图象上，有点 P1，P2，P3 ，P4 它们的横坐标依次为1、2、3、4，分别过这些点作 x 轴与 y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为1 S，2S，3S，则S1  S2  S3 

2

3

.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

106 数学加分宝9 上《天天练》第12 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.反比例函数 2

2 (2 1)   

k y k x 在每个象限内 y 随 x 的增大而增大，则 k= −1 .

2.反比例函数 10

2 ( 2)

  

m y m x 的图象分布在第二、四象限内，则 m的值为−3 ．二.（本题满分 10 分）

保护生态环境，建设绿色社会已经从理念变为人们的行动.某化工厂 2021 年1 月的利润为200 万元.设2021年 1 月为第 1 个月，第 x 个月的利润为 y 万元.由于排污超标，该从 2021 年1 月底起适当限产，并投入资金进行治污改造，导致月利润明显下降，从 1 月到 5 月， y 与 x 成反比例.到5 月底，治污改造工程顺利完工，从这时起，该厂每月的利润比前一个月增加 20 万元（如图）. （1）分别求该化工厂治污期间及改造工程顺利完工后 y 与 x 之间对应的函数关系式. （2）治污改造工程顺利完工后经过几个月，该厂利润才能达到 200 万元？

（3）当月利润少于 100 万元时为该厂资金紧张期，问该厂资金紧张期共有几个月？（1） （1 5）

200   x 

x

y y  20x  6（0 x＞5）（2）8 （3）5

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

107 数学加分宝三.（本题满分 10 分）

如图，已知一次函数 y  kx  b(k  0) 的图象与反比例函 ( 0) 8   m

x

y 的图象交于A，B两点，且A点的横坐标与 B 点的纵坐标都是－2.求：

（1）一次函数的关系式；

（2） AOB 的面积. （1） y  x  2 （2）6

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

108 数学加分宝9 上《天天练》第12 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1.反比例函数 ( )

2 7

2 5 － m －m－

y= m x 的图象在每一象限内 y 随 x 的增大而增大，则m= −2 .

2.若反比例函数

x

k

y  3  的图象在一、三象限内，正比例函数 y  (2k  9)x 过二、四象限，则k的整数值是 4 ；

二.（本题满分 10 分）

近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO.在一次矿难事件的调查中发现：从零时起，井内空气中CO 的浓度达到 4mg / L ，此后浓度呈直线型增加，在第7 小时达到最高值46mg / L ，发生爆炸；爆炸后，空气中的CO 浓度成反比例下降.如图所示，根据题中相关信息回答下列问题：

（1）求爆炸前和爆炸后空气中CO 浓度 y 与时间 x 的函数关系式，并写出相应的自变量取值范围；（2）当空气中的CO 浓度达到34mg / L 时，井下3km 的矿工接到自动报警信号，这时他们至少要以多少km / h 的速度撤离才能在爆炸前逃生？

（3）矿工只有在空气中的CO 浓度降到 4mg / L 及以下时，才能回到矿井开展生产自救，求矿工至少在爆炸后多少小时才能下井？

（1） （ ）； （ ＞7）322

6 4 0 7 x

x

y  x   x  y  （2）1.5km/ h （3）73.5 小时

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

109 数学加分宝三.（本题满分 10 分）

如图，已知一次函数 y  x  8 和反比例函数

x

k

y  的图象在第一象限内有两个不同的公共点A、B.（1）求实数 k 的取值范围；

（2）若 AOB 的面积为 24，求 k 的值. （1） 0＜k＜16 （2）7

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

110 数学加分宝9 上《天天练》第12 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1.已知反比例函数

x

m

y

1 2  的图象上有 A（ x1 ，y1 ）、B（ 2 x ， 2 y ）两点，当x1 ＜2 x＜0 时，y1 ＜2y，则 m 的取值范围是（ D ）

A. m ＜0 B. m ＞0 C. m ＜

2

1

D. m＞

2

1

2.在函数

x

k

y

2

2  

 （ k 为常数）的图象上有三个点（−2， 1 y ），(−1， 2 y )，（21，3 y），函数值1y，2y，3 y 的大小关系为 y3<y1<y2 .二.（本题满分 10 分）

制作一种产品,需先将材料加热达到 60℃后,再进行操作.设该材料温度为 y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度 y 与时间 x 成一次函数关系;停止加热进行操作时,温度y 与时间x成反比例关系(如图所示).已知该材料在操作加工前的温度为 15℃，加热 5 分钟后温度达到60℃. （1）分别求出将材料加热和停止加热进行操作时，y 与 x 的函数关系式；

（2）根据工艺要求，当材料的温度低于 15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间?

（3）根据工艺要求，当材料的温度不低于 30℃时，为最佳操作时间，那么此工艺品的最佳操作时间为多久?（1）

x

y x y

300

9 15, 1   2  ；（2）当 y=15,则 x=20；

（3）当 y1=30，x= 3

5 ，y2=30，x=10， ∴最佳操作时间为 10－ 3

5

= 3

25 分钟

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

111 数学加分宝三.（本题满分 10 分）

如图，已知 A(4，n) ， B(2， 4) 是一次函数 y  kx  b 的图象和反比例函数xmy 的图象的两个交点.（1）求反比例函数和一次函数的关系式；

（2）求直线 AB 与 x 轴的交点C 的坐标及 AOB 的面积；

（3）求不等式 ＜0

x

m

kx  b  的解集（请直接写出答案）. （1）

x

y

8   ， y  x  2 ；（2）C(2，0) ，  6 AOB S ；（3）  4  x 0 或x 2

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

112 数学加分宝9 上《天天练》第12 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.已知反比例函数  (k  0)

x

k

y 的图象上有两点 A（ 1 x ， 1 y ），B （ 2 x ，2 y ），且1 2 x＜x，则12yy的值是（ D ）

A.正数 B.负数 C.非正数 D.不能确定

2.如图，点 C 在反比例函数  (x  0)

x

k

y 的图象上，过点 C 的直线与 x 轴，y 轴分别交于点A、B，且AB=BC，△AOB 的面积为 2，则 k 的值为（ D ）

A.1 B.2 C.4 D.8

二.（本题满分 10 分）

已知一次函数 y  kx  b 和反比例函数

x

m

y  在同一平面坐标系内交于A、B两点，且A（－6，n），B （3，－6）；

①求 m 、 n 的值；

②求 AOB 的面积；

③根据图象直接写出当 x 取何值时，一次函数值大于反比例函数值. ① m  18 n  3 ②13.5 ③ x＜ 6 或 0＜x＜3

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

113 数学加分宝三.（本题满分 10 分）

如图，已知函数

x

k

y  （ x＞0 ）的图象经过点 A 、B ，点 A 的坐标为（1，2），过点A作AC// y轴，AC1（点C 位于点 A 的下方），过点C 作CD // x 轴，与函数的图象交于点 D，过点B作BECD，垂足E在线段CD 上，连接OC 、OD . （1）求 OCD 的面积；

（2）当 BE AC

2

1  时，求CE 的长. （1）

2

1 （2）

3

1

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

114 数学加分宝9 上《天天练》第12 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1.如图，在 x 轴上点 P 的右侧有一点 D，过点 D 作 x 轴的垂线交双曲线x

y

1  于点B，连结BO交AP于C，设∆AOP 的面积为 S1，梯形 BCPD 面积为 S2，则 S1与 S2的大小关系是 S1 > S2.（选填“>”“<”或“＝”）2.如图， A 、 B 是双曲线

x

k

y  两点，过 A 点作 AC  x 轴，交OB 于 D点，垂足为C.若ADO的面积为 1， D 为OB 的中点，则 k 的值为（ B ）

A. 3

4

B. 3

8

C.3 D.4

二.（本题满分 10 分）

如图， RtABO 的顶点 A 是双曲线

x

k

y  与直线 y  x  (k 1)在第二象限的交点，ABx轴于B且2

3

SABO  . （1）求这两个函数的关系式；

（2）求直线与双曲线的两个交点 A ，C 的坐标和 AOC 的面积. （1）

x

y

3   y  x  2 （2） A （－1，3） C （3，－1） 4

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

115 数学加分宝三.（本题满分 10 分）

如图，矩形ABCD的两边AD，AB的长分别为3和8，E是DC的中点，反比例函数x

my =的图象经过点E，与AB交于点F. （1）若点 B 坐标为（−6，0），求 m 的值及图象经过 A，E 两点的一次函数的关系式；（2）若 AF−AE=2，求反比例函数的关系式.

x

m y x m y

4

(2) 4

3

4

(1) 12 

  ，   ；   ， 

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

116 数学加分宝9 上《天天练》第13 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1．已知 Rt△ABC 中，∠C＝90°，AC＝2，BC＝3，那么下列各式中正确的是（C ）A．sinA＝

3

2

B．tanA＝

3

2

C．tanB＝

3

2

D．cosB＝322．如图，Rt△ABC 中，∠C＝90°，AC＝2BC，则 cosB 的值为（ A ）

A．

5

5

B．

2

1

C．

5

2 5

D．2

二.（每题 5 分，共 10 分）

1．如图，在△ABC 中，∠C＝90°，AB＝5，AC＝4，下列三角函数表示正确的是（B ）A．

5

4

sin A  B．

5

4

cos A  C．

3

4

tan A  D．

54tan B2．在 4×4 网格中，∠α的位置如图所示，则 tan 的值为（ C ）

A．

5

2 5

B．

5

5

C．2 D．

2

1

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

117 数学加分宝三.（每题 5 分，共 10 分）

1．如图，在 4×4 的正方形网格中，tanα的值等于（ C ）

A．

13

2 13

B．

13

3 13

C．

2

3

D．

3

2

2．如图，在 Rt△ABC 中，∠C＝90°，BC＝1，AC＝ 3 ，求 tanA 与 tanB 的值．, tan 3

3

3

tan A  B 

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

118 数学加分宝9 上《天天练》第13 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1．2tan30°的值等于（ B ）

A． 3 B．

3

2 3

C．

2

2

D．

2

1

2．下列三角函数的值是

2

3 的是（ A ）

A．cos30° B．tan30° C．cos45° D．sin30°二.（每题 5 分，共 10 分）

1．x 为锐角，

3

2

sin x  ，则cos x 的值为（ B ）

A．

9

7

B．

3

7

C． 7 D．

3

2

2．在 Rt△ABC 中，∠C＝90°，若 sinA＝

3

2 ，则 cosA＝（ C ）

A．

3

13

B．

2

13

C．

3

5

D．

2

5

三.（每题 5 分，共 10 分）

1．在 Rt△ABC 中，∠C＝90°，那么 sinA+cosA 的值是（ A ）

A．大于 1 B．小于 1 C．等于 1 D．不能确定2．已知   3

3

tan 90   ，则锐角 的度数是（ A ）

A．60° B．45° C．30° D．75°

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

119 数学加分宝9 上《天天练》第13 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1．如图，在 Rt△ABC 中，∠C＝90°，cosA＝

3

1 ，则 sinB 的值为（ B ）A．

2

1

B．

3

1

C．

3

2 3

D． 2 22．若sin70   cos50 ，则 的度数是（ B ）

A．20° B．30° C．40° D．50°二.（每题 5 分，共 10 分）

计算：（1）

  

   2sin 60 cos 60

tan 60 2cos 45

2

2

（2） 2 tan 60  tan 45  4cos30 ＝3+ ； ＝1．

三.（每题 5 分，共 10 分）

1．如图，某博物馆大厅电梯的截面图中，AB 的长为 12 米，AB 与 AC 的夹角为α，则高BC是（A）A．12sin 米 B．12cos 米 C．

sin

12 米 D．

cos12米2．如图，已知 Rt△ABC，CD 是斜边 AB 边上的高，那么下列结论正确的是（D ）A．CD＝AB•tanB B．CD＝AD•cosA C．CD＝AC•sinB D．CD＝BC•cosA

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

120 数学加分宝9 上《天天练》第13 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1．在平面直角坐标系中，第一象限内射线 OA 与 x 轴正半轴的夹角为α，点 P 在射线OA 上，若54cos，则点 P 的坐标可能是（ D ）

A．（3，5） B．（5，3） C．（3，4） D．（4，3）2．如图，已知在平面直角坐标系 xOy 内有一点 A（2，3），那么 OA 与 x 轴正半轴的夹角α的余弦值是（D）A．

2

3

B．

3

2

C．

13

3 13

D．

132 13二.（每题 5 分，共 10 分）

1．如图，在△ABC 中，∠B＝45°，AD⊥BC 交 BC 于点 D，若 AB＝ 4 2 ，tan∠CAD＝43，则BC＝（C）A．6 B．6 2 C．7 D．7 22．如图，在 Rt△ABC 中，∠ACB＝90°，CD⊥AB，D 为垂足．若 AC＝8，BC＝6，则sin∠ACD=（C）A．

3

4

B．

4

3

C．

5

4

D．

5

3

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

121 数学加分宝三.（每题 5 分，共 10 分）

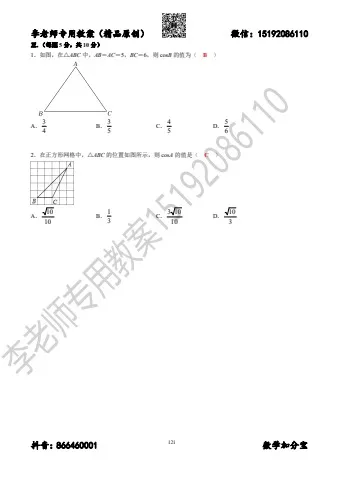
1．如图，在△ABC 中，AB＝AC＝5，BC＝6，则 cosB 的值为（ B ）

A．

4

3

B．

5

3

C．

5

4

D．

6

5

2．在正方形网格中，△ABC 的位置如图所示，则 cosA 的值是（ C ）

A．

10

10

B．

3

1

C．

10

3 10

D．

3

10

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

122 数学加分宝9 上《天天练》第13 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1．如图．在 5×4 的正方形网格中，△ABC 的顶点都在格点上，则 sin∠BAC 的值为（A）A．

5

4

B．

5

3

C．

4

3

D．

3

2

2．如图，△ABC 的顶点是正方形网格的格点，则 sin∠ACB 的值为（ D ）A．3 B．

3

1

C．

10

10

D．

103 10二.（每题 5 分，共 10 分）

1．某滑雪场举办冰雪嘉年华活动，采用直升机航拍技术拍摄活动盛况，如图，通过直升机的镜头C观测到水平雪道一端 A 处的俯角为 30°，另一端 B 处的俯角为 45°．若直升机镜头 C 处的高度CD为200 米，点A、D、B 在同一直线上，则雪道 AB 的长度为（ B ）

A．200 米 B．（ 200  200 3 ）米

C．600 米 D．（ 200  200 2 ）米

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

123 数学加分宝2．如图，某数学兴趣小组测量一棵树 CD 的高度，在点 A 处测得树顶 C 的仰角为45°，在点B处测得树顶C 的仰角为 60°，且 A，B，D 三点在同一直线上，若 AB＝16m，则这棵树 CD 的高度是（A）A．83 3m B．83 3m C．63 3m D．633m

三.（每题 5 分，共 10 分）

1．如图所示，河堤横断面迎水坡 AB 的坡度 i＝1：2，堤高 BC＝6m，则坡面AB 的长度是（D）A．6m B．12 m C．6 3 m D．6 5m

2．如图大坝的横断面，斜坡 AB 的坡比 i＝1:2，背水坡 CD 的坡比 i＝1:1，若坡面CD 的长度为62米，则斜坡 AB 的长度为（ C ）

A． 4 3 米 B．6 3 米 C．6 5 米 D．24 米

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

124 数学加分宝9 上《天天练》第14 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.如图，已知△ABC 中，AB=9，BC=6，△ABC 的面积等于 9，求 tanB，sinB，cosB. 【答案】解：

3

2 2

cos

3

1

sin

4

2

tan B  ， B  ，B 

2.如图，在四边形 ABCD 中，∠B=∠D=90°，AB=3，BC=2，

4

tan

3

A  ，则 CD 的值为1.2 .二.（本题满分 10 分）

（21 年西海岸一模）某住宅小区有平行建设的南、北两栋高层建筑．冬至日正午，南楼在北楼墙面上形成的影子 AF 的高度为 42 米，此时太阳高度角（即正午太阳光线与水平面的夹角）∠CAB＝35°，夏至日正午，南楼在水平地面形成的影子与北楼的距离 DF 为 80 米，此时太阳高度角∠CDE＝80°．求两楼间的距离．（参考数据：sin 35°≈0.57，cos 35°≈0.82，tan 35°≈0.7，sin80°≈0.98，cos 80°≈0.175，tan80°≈5.6）解：根据题意，设两楼之间的距离为 x 米，

由题得四边形 ABEF 是矩形，∠CAB=35°，∠CDE=80°，

FD=80 米，AF=42 米，在 Rt△ABC 中，  BC  x  tan 35 ，

在 Rt△DEC 中，   CE  DE  tan80  (x  80) tan80 ，

又 BE=AF=42，BE=CE－CB，

所以(  80) tan80  tan 35  42

  x x ，解得 x 100

答：两楼之间的距离为 100 米.....................6 分

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

125 数学加分宝三.（本题满分 10 分）

（18 年青大附一模）如图，在楼房 AB 和塔CD 之间有一棵树 EF ，从楼顶 A处经过树顶E点恰好看到塔的底部点 D ，且俯角 为  45 .从距离楼底 B 点 1 米的 P 点处经过树顶 E 点恰好看到塔的顶部C点，且仰角为  30 .已知树高 EF  6 米，求塔 CD 的高度.（结果保留根号）

【答案】6  2 3 米

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

126 数学加分宝9 上《天天练》第14 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1.（16 年李沧期末）如图，在边长相同的小正方形网格中，点 A、B、C、D 都在这些小正方形的顶点上，AB，CD 相交于点 P，则 tan APD  2 . 2.如图，在正方形方格纸中，每个小正方形的边长都相等，A、B、C、D 都在格点处，AB与CD相交于点P，则 cos∠APC 的值为

5

2 5

.二.（本题满分 10 分）

（2019 年市南一模）如图，要测量一垂直于水平面的建筑物 AB 的高度，小明从建筑物底端B出发，沿水平方向向右走 30 米到达点C ，又经过一段坡角为 30°，长为 20 米的斜坡CD，然后再沿水平方向向右走了50 米到达点 E（ A、B、C、D、E 均在同一平面内）.在 E 处测得建筑物顶端A的仰角为24°，求建筑物AB的高度.（结果保留根号，参考数据：sin24°≈ 5

2 ，cos24°≈ 10

9 ，tan24°≈ 20

9 ）【答案】 3

2

9

26 

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

127 数学加分宝三.（本题满分 10 分）

（20 年平度一模）如图， EF 表示一座风景秀美的观景山， AC，CE是已经修好的登山步行道．该景区为方便老年游客登顶观景，欲在山脚 A 与山顶 E 之间架设一条登山索道 AE．在山脚A处测得点C的仰角为 24°，在C 处测得山顶 E 的仰角为 45°，在山脚 A 处测得山顶 E 的仰角为 37°．已知步行道AC长640米，则新架设的索道 AE 长多少米？

（参考数据：

5

2

sin24  ，

10

9

cos24  ，

20

9

tan24  ，

5

3

sin37  ，54cos37 ，43tan37）解：在 Rt△ABC 中，BC=AC×sin∠CAB=AC×sin24°=640×

5

2

=256 ；

AB=AC×cos∠CAB=AC×cos24°=640×

10

9

=576；过点 C 作 CB⊥AF 于点 B，作CD⊥EF 于点D易证，四边形 CBFD 是矩形，∴DF=BC，CD=BF，设 CD 长为 x 米，在 Rt△CDE 中，DE=CD×tan45°=x在 Rt△AEF 中∵ tan

EF

EAF

AF

  ，∴ EF  AF  tan 37 ，∴

3

256 576

4

x   （x  ），∴x=704 ，∴EF=ED+DF=704+256=960 在 Rt△AEF 中，∵sin

EF

EAF

AE

  ，∴

9601600sin 35EFAE

EAF 因此，新架设索道 AE 长约为 1600 米．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

128 数学加分宝9 上《天天练》第14 周③答案（满分30 分）一.（每题 5 分，共 10 分）

（20 年胶州一模）为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i＝1:2.4 的山坡 AB 上发现有一棵古树 CD．测得古树底端C 到山脚点A的距离AC＝26 米，在距山脚点 A 水平距离 6 米的点 E 处，测得古树顶端 D 的仰角∠AED＝48°（古树CD与山坡AB的剖面、点 E 在同一平面上，古树 CD 与直线 AE 垂直），则古树 CD 的高度约为多少米？（参考数据：sin48°≈0.73，cos48°≈0.67，tan48°≈1.11）

二.（本题满分 10 分）（20 年青大附一模）图 1 是安装在倾斜屋顶上的热水器，图2 是安装热水器的侧面示意图，已知屋面 AE 的倾斜角EAD 为 22°，长为 2 米的真空管 AB与水平线AD的夹角为37°，安装热水器的铁架竖直管CE 的长度为 0.5 米. （1）真空管上端 B 到水平线 AD 的距离. （2）求安装热水器的铁架水平横管 BC 的长度（结果精确到 0.1 米）

（参考数据：

5

3

sin37  ，

5

4

cos37  ，

4

3

tan37  ，

8

3

sin22  ，

1615cos22 ，52tan22）【答案】（1） 1.2 米 （2） BC  0.15  0.2米

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

129 数学加分宝三.（本题满分 10 分）

（21 年城阳一模）如图,已知 B 港口位于 A 观测点东偏北 67°(即∠DAB=67。)方向,且B 到A观测点正东方向的距离 BD 长为 46 海里,一般货轮从 B 港口以 40 海里/h 的速度沿∠ABC=45°的BC 方向航行,现测得货轮C 处位于 A 观测点东偏北 82°(即 。 DAC  82 ）方向,求此时货轮 C 到 AB 之间的最短距离(精确到0.1海里). (参考数据:sin67°  0.92,cos67°  0.39,tan67°  2.36,sin82°  0.99,cos82  0.14tan82° 7.12,sin15° 0.26, cos15° 0.97，tan15° 0.27）

【答案】解:过 C 作 CH⊥AB 于 H，在 RT▲ABD 中,∵BD=46,∠BAD=67°∴AB= 500.9246sin67 BD∵∠ABC=45°∴CH=BH∵∠DAC=82°∴∠CAB=15°,设 CH=BH=x, ∴AH=

tan15 0.27

CH x  ∴ 50

0.27

 

x

x

解得:x=10.6,∴货轮 C 到 AB 之间的最短距离是 10.6 海里

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

130 数学加分宝9 上《天天练》第14 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.（20 年崂山期末）平面直角坐标系中，将抛物线 2

y  2x 先向左平移 2 个单位，再向下平移1 个单位，得到的抛物线的表达式是（B ）

A. 2( 2) 1

2

y   x  

B. 2( 2) 1

2

y   x  

C. 2( 2) 1

2

y   x  

D. 2( 2) 1

2

y   x  

2.（15 年市南期末）将抛物线 2

y  (x 1)  3向左平移 1 个单位，再向下平移3 个单位后所得抛物线的关系式为（ D ）

A． 2

y  (x  2)

B． 2

y  (x  2)  6

C． 2

y  x  6

D． 2

y  x

二.（每题 5 分，共 10 分）

1（. 17 年市南期末）把抛物线 2 y  (x 1) 向下平移 2 个单位，再向右平移 1 个单位，所得到的抛物线是（D）A. 2 y  (x  2)  2

B. 2 y  (x  2)  2

C. 2 y  x  2

D. 2 y  x  2

2.（16 年市北期末）抛物线  

2 y  x  2  3可由抛物线 2 y  x 通过平移得到，平移过程正确的是（B）A.先向左平移 2 个单位，再向上平移 3 个单位

B.先向左平移 2 个单位，再向下平移 3 个单位

C.先向右平移 2 个单位，再向下平移 3 个单位

D.先向右平移 2 个单位，再向上平移 3 个单位

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

131 数学加分宝三.（每题 5 分，共 10 分）

1.（15 年市南期末）抛物线 2

y  x  2x 1的顶点坐标是（ A ）

A．（1，0） B．（−1，0） C．（−2，1） D．（2，−1）2.（17 年李沧期末）二次函数 y  ax  bx  c

2 （ a  0 ）的图象如图所示，下列说法中不正确的是（ D ）

A. 4 0 b

2  ac＞ B. a＞0 C. c＞0 D. 0

2

＜a

b 

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

132 数学加分宝9 上《天天练》第14 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1（. 14 年市北期末）已知反比例函数

x

k

y  的图象如图所示，二次函数 2 2

y  2kx  x k 的图象大致为（D）2.（14 年 39 中期末）在反比例函数

k

y

x  中，当 x  0 时，y 随 x 的增大而增大，则二次函数2ykx2kx图象大致是（ D ）

A. B. C. D.二.（每题 5 分，共 10 分）

1.（14 年李沧期末）函数 ( 1) 2

y  k x  与函数

x

k

y  在同一坐标系中的图象大致是（A ）A B C D

2.（18 年李沧期末）在同一平面直角坐标系中，反比例函 y= b

x

（b≠0）与二次函数y=ax

2+bx（a≠0）的图象大致是（ D ）

A. B. C. D.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

133 数学加分宝三.（每题 5 分，共 10 分）

1.（13 年李沧期末）如图是二次函数 2

y  ax  bx  c 图象的一部分，其对称轴是x=1，且过点(3,0)，下列说法：① abc  0 ；② 2a  b  0 ；③ 4a  2b  c  0 ；④若 1 (5, y ) ， 2 (1, y ) 是抛物线上两点，则12yy；其中说法正确的是（ D ）

A.①② B.②③ C.①②④ D.①②③④

2.（16 年市北期末）如图，抛物线  

2 y  ax  bx  c a  0 的对称轴为直线 x 1，与x轴的一个交点坐标为1,0，其部分图象如图所示，则下列结论中正确的有（ A ）个. ① 2 4ac  b ； ②当 x  0 时， y 随 x 增大而增大；

③当 x  0 或 x  2 时， y  3； ④ a  b  c  0 . A. 4 个 B. 3 个 C. 2 个 D. 1 个

-1 0 1

x

y

3

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

134 数学加分宝9 上《天天练》第15 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.（16 年李沧期末）抛物线 y  ax  bx  c

2 的图象如图所示，则一次函数 y ax b与反比例函数xcy在同一平面直角坐标系内的图象大致为（ B ）

A. B. C. D.

2.（17 年市北期末）已知二次函数  0

2

y  ax  bx  c a  的图象如图所示，且关于x的一元二次方程0

2

ax  bx  c  m  没有实数根，则下列结论① 4 0

2 b  ac  ；② ac  0 ；③m2正确的有（D）个.A. 0 B.1 C.2 D.3

二.（本题满分 10 分）（17 年青大附二模 22）

如图，一大桥的桥拱为抛物线形，跨度 AB =50 米，拱高（即拱桥最高点C到水面AB的距离）为20米.（1）求桥拱所在抛物线的表达式. （2）当水面再上涨 12 m 将达到警戒水位，求达到警戒水位时水面的宽度.

（1）  

2 25

125

4

y   x  （2）10 10

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

135 数学加分宝三.（本题满分 10 分）（2019 年市北二模 22）

如图是甲、乙两人进行羽毛球练习赛时的一个瞬间，羽毛球飞行的高度 y(m)与水平距离x(m)的路线为抛物线的一部分，如图，甲在 O 点正上方 1m 的 P 处发出一球，已知点 O 与球网的水平距离为5m，球网的高度为 1.55 米，羽毛球沿水平方向运动 4m 时，达到羽毛距离地面最大高度是

3

5

m. （1）求羽毛球经过的路线对应的函数关系式；

（2）通过计算判断此球能否过网；

（3）若甲发球过网后，羽毛球飞行到离地面的高度为

24

31

m 的 Q 处时，乙扣球成功. 求此时乙与球网的水平距离. （1）羽毛球经过的路线对应的函数关系式：

3

5

( 4) 24

1 2

y   x   . （2）x=5 时， 1.625 1.55

24

39

y    ，能过网. （3）

24

31

y  时，x=7，x=1（舍），7—5=2（米），乙距离球网 2 米.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

136 数学加分宝9 上《天天练》第15 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1.（13 年市北期末）已知点 (1 )

1 A ，y 、 ( 2 )

2 B  ，y 、 ( 2 )

3 C  ，y 在函数

21212

y x的图象上，则1y、2 y 、 3 y 的大小关系是（ D ）

A. 2 3 1 y  y  y B. 1 2 3 y  y  y C. 1 3 2 y  y  y D. 3 2 1 y yy2.（18 年市北期末）已知二次函数 y=kx²+k(k≠0)与反比例函数 y= x

k

(k≠0)，它们在同一直角坐标系中的图象大致是（ D ）

A. B. C. D.二.（本题满分 10 分）（2019 年市南二模 22）

如图，斜坡 AB 长 10 米，按图中的直角坐标系斜坡可用 5

3

3

y   x  表示，点A、B分别在x轴和y轴上.在坡上的 A 处有喷灌设备，喷出的水柱呈抛物线形落到 B 处，抛物线可用y xbxc2

31表示. （1）求抛物线的函数关系式（不必写自变量取值范围）；

（2）求水柱离坡面 AB 的最大高度；

（3）在斜坡上距离 A 点 2 米的C 处有一棵 3.5 米高的树，水柱能否越过这棵树？（1） 3 5

3

4

3

1 2

y   x  x  （2）

4

25 米 （3）能

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

137 数学加分宝三.（本题满分 10 分）

（19 年市南期末）某商场销售一种小商品， 进货价为 5 元/件.售价为 6 元/件时，每天的销售量为100件.在销售过程中发现：销售单价每上涨 0.5 元，每天的销售量就减少 5 件.设销售单价为x元/件（x6），每天销售利润为 w 元. （1）求 w 与 x 的函数关系式；

（2）要使每天销售利润不低于 280 元，求销售单价所在的范围；

（3）若每件文具的利润不超过 60%，则每件文具的销售单价定为多少元时，每天获得的利润最大，最大利润是多少？

解：（1）   10 210 800

0 5

6

5 100 5

2     









 

    x x

x

w x .故 y 与 x 的函数关系式为： 10 210 800

2 w   x  x  （2）要使当天利润不低于 280 元，则 y≥280，

∴ 10 210 800 10  10 5 302 5 280

2 2 w   x  x     x  .  . 解得， x1  9， x2 12，∵﹣10＜0，抛物线的开口向下，

∴当天销售单价所在的范围为 9≤x≤12，当天销售利润不低于280 元（3）∵每件文具利润不超过 60%

∴ 0 6

5

5  .

x  ，得 x≤8，∴文具的销售单价为 6≤x≤8，

由（1）得 10 210 800 10  10.5 302.5

2 2

w   x  x     x  

∵对称轴为 x＝10.5，∴6≤x≤8 在对称轴的左侧，且 w 随着 x 的增大而增大∴当 x＝8 时，取得最大值，此时 10 9 10.5 302.5 240

2

w      即每件文具售价为 8 元时，最大利润为 240 元

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

138 数学加分宝9 上《天天练》第15 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1.（19 年市南期末）二次函数 y  ax  bx  c

2 的图象如图所示，以下结论：①abc0；②24acb；③ 2a  b  0 ；④其顶点坐标为（

2

1 ，－2）； ⑤当

2

1

x  时， y 随 x 的增大而减小；⑥abc0中,正确的有（ B ）

A.3 个 B.4 个 C.5 个 D. 6 个

2.（18 年市南期末）如图，已知顶点为（−3，−6）的抛物线 y=ax

2+bx+c 经过点（−1，−4），下列结论：①b

2＞4ac；②ax

2+bx+c≥−6；③若点（−2，m），（−5，n）在抛物线上，则m＞n；④关于x 的一元二次方程 ax

2+bx+c=−4 的两根为−5 和−1，其中正确的有（ C ）

A.1 个 B.2 个 C.3 个 D.4 个

二.（本题满分 10 分）（19 年崂山育才二模 22）

如图，某公园要修建一个截面为抛物线的拱门，其最大高度为 4.5 米，宽度OP 为6 米，现以地面（OP所在直线）为 x 轴建立直角坐标系. （1）求这条抛物线所对应的函数表达式；

（2）如图 1，公园想在抛物线拱门距地面 3 米处钉两个钉子以便拉一条横幅，请计算该横幅宽度为多少米？（3）为修建该拱门，施工队要搭建一个矩形“支撑架”ABCD，（由四根木杆AB－BC－CD－DA组成），使C，B 两点在抛物线上，A，D 两点在地面 OP 上，则施工队最多需要多少米该种木杆？（1）  3 4.5

2

1 2

y   x   ；（2） 2 3 ；（3）13 米

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

139 数学加分宝三.（本题满分 10 分）（18 年育才二模 22）

施工队要修建一个横断面为抛物线的公路隧道，其最大高度为 6 米，宽度OM为12 米，现在O点为原点，OM 所在直线为 x 轴建立直角坐标系如图所示．

（1）直接写出点 M 及抛物线顶点 P 的坐标；

（2）求出这条抛物线的函数解析式；

（3）施工队计划在隧道门口搭建一个矩形“脚手架” ABCD ，使 A、D点在抛物线上，B、C点在地面OM上，为了筹备材料，需求出“脚手架”三根木杆 AB、AD、DC 的长度之和的最大值是多少？请你帮施工队计算一下．

（1）P(6,6) M（12,0）

（2） y x 2x

6

1 2   

（3） 2 12

3

1 2

y   t  t  当 t=3 时 y=15

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

140 数学加分宝9 上《天天练》第15 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.（16 年市南期末）下列表格中的数据是二次函数 y  ax  bx  c

2 的几组对应值.根据表中数据我们可以判断，当 0

2

ax  bx  c  时，自变量 x 的取值范围是（ B ）

x ... −1 0 1 2 3 4 ...

y ... 0 −3 −4 −3 0 5 ... A. x 1 B. x  1或 x  3 C. x  5 D. 1 x 3

2.（19 年市北期末）如图，二次函数 y  ax  c

2 的图象与反比例函数

x

c

y  的图象相交于点A（123，），则关于 x的不等式

x

c

ax  c 

2 的解集为（ D ）

A. 2

3

x   B. 2

3

x   C. 1

2

3   x  D. 2

3

x < - 或x 0二.（本题满分 10 分）

（17 年李沧期末）某公司营销 A ， B 两种产品，根据市场调研，确定两条信息：信息 1：销售 A 种产品所获利润 y （万元）与所售产品 x （吨）之间存在二次函数关系，如图所示：信息 2：销售 B 种产品所获利润 y （万元）与销售产品 x （吨）之间存在正比例函数关系y0.3x．根据以上信息，解答下列问题；

（1）求二次函数的表达式；

（2）该公司准备购进 A 、 B 两种产品共 10 吨，请设计一个营销方案，使销售A、B两种产品获得的利润之和最大，最大利润是多少万元？

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

141 数学加分宝三.（本题满分 10 分）

（16 年李沧期末）某片果园有果树 80 棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低.若该果园每棵果树产果y（千克），增种果树 x （棵），它们之间的函数关系如图所示. （1）求 y 与 x 之间的函数关系式；

（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实 7000 千克？（3）当增种果树多少棵时，果园的总产量 w （千克）最大？最大产量是多少？

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

142 数学加分宝9 上《天天练》第15 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1.（15 年市北期末）一个足球被从地面向上踢出，它距地面的高度 hm与足球被踢出后经过的时间ts之间具有函数关系 h at 19.6t 2   ，已知足球被踢出后经过 4 s 落地，则足球距地面的最大高度是19.6m．2.（19 年市北期末）体育公园的圆形喷水池的中央竖直安装了一个柱形喷水装置OA，A处为喷头向外喷水，水流在各方向上沿形状相同的抛物线路径落下（如图 1），A 点距离水平面为49米，即OA=49米，如果曲线 APB 表示的是落点 B 离 O 最远的一条水流（如图 2），水流喷出的高度y（米）与水平距离x（米）之间的关系式是 y  ax  bx  c

2 （x>0），该抛物线的顶点是（

4

25

2，），那么圆形水池的半径至少为___4.5______米，才能使喷出的水流不至于落在池外.二.（本题满分 10 分）（20 年李沧二模 22）

某游乐园有一个直径为 16 米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为批物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合,如图所示,以水平方向为x 轴,喷水池中心为原点建立直角坐标系. （1） 求水柱所在抛物线（第一象限部分）的函数表达式；

（2）王师傅在水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高 1.8 米的王师傅站立时必须在离水池中心多少米以内？

（3） 经检修评估,游乐园决定对喷水设施做如下设计改进；在喷出水柱的形状不变的前提下,把水池的直径扩大到 32 米,各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合,请探究扩建改造后喷水池水柱的最大高度.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

143 数学加分宝三.（本题满分 10 分）（20 年市南二模 22）

发石车是古代远程攻击的武器，现有一发石车，发射出去的石块沿抛物线轨迹运行，距离发射点20米时达到最大高度 10 米.如图所示，现将发石车放置在山坡底部 O 处，山坡上有一点A，距离O的水平距离为30米，垂直高度为 3 米，AB 是高度为 3 米的防御墙. （1）求石块运行的函数关系式；

（2）计算说明石块能否飞越防御墙 AB；

（3）石块飞行时与坡面 OA 之间的最大距离是多少？

（4）如果发石车想恰好击中点 B，那么发石车应向后平移多远？

（1）

( 20) 10..................3分

40

1

y

....................................2分40

1

(0,0) a设: ( 20) 10....................1分

2

1

2

1     

  

  

x

y a x  在图像上，

（2）（0,0）（30,3）在直线 OA 上，∴y2=.01x …………………………………………4 分设石块与坡面的距离为 w 米，w=y1-y2= ( 18) 8.1

40

1 2  x   ……………………….5 分0 w 8.1

40

1

  ，开口向下，有最大值， 答：最大距离为 8.1 米…………………………………..6 分

（3）当 x=30 时，W=4.5>3……………………………..7 分，所以，能飞越……………………………8分（4）当 y1=6 时

( 20) 10. 6 20 4 10., 20 4 10( ).......................9分40

1

y 1 2

2  1   x    ，x   x   舍去20  4 10.  30  4 10 10 ，答：后移（4 10. 10）,米………………..10 分