—107 — —108 — 第一章 综合测试卷
第一章 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.下列两组角的终边不相同的是(其中k∈Z) ( )
A.
5π
12
+kπ与7π
12
+kπ B.-
2π
3
+2kπ与
4π
3
+2kπ
C.
π
6
+2kπ与
13π
6
+2kπ D.
π
4
+kπ与±
π
4
+2kπ
2.若函数y=f(x)与y=cosx 的图象关于x 轴对称,则y=f(x)
的解析式为 ( )
A.y=cos(-x) B.y=-cosx
C.y=cos|x| D.y=|cosx|
3.已知角α 的终边经过点P(8,-m),且cosα=
24
5m
,则tanα 的值为
( )
A.±
3
4
B.-
3
4
C.-
4
3
D.±
4
3
4.已知圆心角为60°的扇形内部有一个圆C 与扇
形的半径及圆弧均相切,当圆C 面积为π时,该
扇形的面积为 ( )
A.
π
3
B.
2π
3
C.
π
6
D.
3π
2
5.设地球表面某地正午太阳高度角为θ,ξ为此
时太阳直 射 纬 度,φ 为 该 地 的 纬 度 值,则 有
θ=90°-|φ-ξ|.根据地理知识,某地区的纬
度值约为北纬27.95°,当太阳直射南回归线
(此时的太阳直射纬度为-23.5°)时物体的影子最长,如果在当地
某高度为h0 的楼房北边盖一新楼,要使新楼一层正午的太阳全
年不被前面的楼房遮挡(如图所示),两楼的距离应至少为h0 的
倍.(注意tan38.55°≈0.80) ( )
A.0.5倍 B.0.8倍 C.1倍 D.1.25倍
6.已知定义在区间[0,2π]的函数f(x)=
sinx,sinx≥cosx, cosx,sinx<cosx,
则函
数f(x)≤0的解集是 ( )
A.0,
π
2
?
?
??
?
?
??
B.
π
2
,
3π
2
?
?
??
?
?
??
C.π,
3π
2
?
?
??
?
?
??
D. π,2π
7.函数y=sin2x+
5π 2 的一个对称中心是 ( )
A.
π
8 ,0 B.
π
4 ,0 C.-
π
3 ,0 D.
3π
8 ,0
8.已知函数f(x)=sin(ωx+θ)ω>0,-
π
2
≤θ≤
π 2 的图象相邻的
两个对称中心之间的距离为
π
2
,若将函数f(x)的图象向左平移
π
6
后得到偶函数g(x)的图象,则函数g(x)在下列区间上是单调
递减的是 ( )
A.-
π
3
,
π
6
?
?
??
?
?
??
B.
π
4
,
7π
12
?
?
??
?
?
??
C.
π
2
,
5π
6
?
?
??
?
?
??
D.0,
π
3
?
?
??
?
?
??
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.下列转化结果正确的是 ( )
A.67°30'化成弧度是
3π
8
B.-
10π
3
化成角度是-600°
C.-150°化成弧度是7π
6
D.
π
12
化成角度是15°
10.若角α 的终边与
5π
12
角的终边关于x 轴对称,且α∈(-2π,2π),
则α 的值为 ( )
A.-
5π
12
B.-
19π
12
C.
19π
12
D.
17π
12
11.已知角A,B,C 是锐角三角形ABC 的三个内角,下列结论一定
成立的是 ( )
A.sin(B+C)=sinA B.sin
A+B 2 =cos
C
2
C.sinB<cosA D.cos(A+B)<cosC
12.已知函数f(x)=3sin(2x+φ)-
π
2
<φ<
π 2 的图象关于直线
x=
π
3
对称,则 ( )
A.函数f x+
π 12 为奇函数
B.函数f(x)在
π
3
,
π
2
?
?
??
?
?
??
上单调递增
C.函数f(x)的图象向右平移a(a>0)个单位长度得到的函数
图象关于x=
π
6
对称,则a 的最小值是
π
3
D.若 方 程 f(x)=a 在
π
6
,
2π
3
?
?
??
?
?
??
上 有 2 个 不 同 实 根 x1,x2,则
|x1-x2|的最大值为
π
3
三、填空题:本题共4小题,每小题5分,共20分.
13.若函数f(x)=cosx,x∈[-2π,2π],则不等式xf(x)>0的解
集为 .
14.已知cos
2π
3 +θ =-
7
9
,则sin
π
6 +θ = .
15.水车在古代是进行灌溉引水的工具,是人类的
一项古老的发明,也是人类利用自然和改造自
然的象征,如图是一个半径为 R 的水车,一个
水斗从点 M(2 2,-2 2)出发,沿圆周按逆时
针方向匀速旋转,且旋转一周用时60秒,经过
t秒后,水 斗 旋 转 到 点 N (t,y),其 纵 坐 标 满 足 y=f(t)=
Rsin(ωt+φ), t≥0,ω>0,|φ|<
π
2 ,则函数f(t)的解析式为
,当t∈[10,25]时,函数f(t)的最大
值是 .
16.已知函数y=tanωx+
π 6 的图象关于点
π
3 ,0 对称,且|ω|≤1,
则实数ω 的值为 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)已知一扇形的圆心角为α,半径为R,弧长为l(α>0).
(1)已知扇形的周长为10cm,面积是4cm
2,求扇形的圆心角;
(2)若扇形周长为20cm,当扇形的圆心角α 为多少弧度时,这个
扇形的面积最大?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —109 — —110 —
18.(12分)化简:
cos210°·cos(-420°)·tan330°
tan390°·sin750°·cos900°
.
19.(12分)如图,某地一天4~13时的温度(单位:℃)变化曲线近似
满足函数y=Acos(ωx+φ)+b(A>0,ω>0,0<φ<π)
(1)分别求出A,b,ω,φ 的值;
(2)估计该地当天7时、10时温度各是多少.
20.(12分)如图,弹簧挂着的小球做上下振动,它在t
(单位:s)时相对于平衡位置(静止时的位置)的高度
h(单位:cm)由关系式h=Asinωt+
π 4 确定,其中
A>0,ω>0,t∈[0,+∞).在一次振动中,小球从最
高点运动至最低点所用时间为1s.且最高点与最低
点间的距离为10cm.
(1)求小球相对平衡位置的高度h(单位:cm)和时间t(单位:s)
之间的函数关系;
(2)小球在t0s内经过最高点的次数恰为 50 次,求t0 的取值
范围.
21.(12分)已知函数f(x)=Asin(ωx+φ) A>0,ω>0,|φ|<
π
2
的部分图象如图所示.
(1)求f(x)的解析式;
(2)将y=f(x)图象上所有点的横坐标缩小到原来的
1
2
倍(纵坐
标不变),再将图象上所有点的纵坐标扩大到原来的2倍(横坐
标不变),最后向下平移2个单位,得到y=g(x)的图象,求函数
y=g(x)的解析式及在 R上的对称中心坐标.
22.(12分)长春某日气温y(℃)是时间t(0≤t≤24,单位:小时)的
函数,下面是某天不同时间的气温预报数据:
t(时) 0 3 6 9 12 15 18 21 24
15.7 14.0 15.7 20.0 24.2 26.0 24.2 20.0 15.7
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看
成余弦型函数y=Acos(ωt+φ)+b 的图象.
(1)根据以上数据,试求y=Acos(ωt+φ)+b(A>0,ω>0,0<φ
<π)的解析式;
(2)大数据统计显示,某种特殊商品在室外销售可获3倍于室内
销售的利润,但对室外温度要求是气温不能低于23 ℃.根据(1)
中所得模型,一个24小时营业的商家想获得最大利润,应在什
么时间段(用区间表示)将该种商品放在室外销售,单日室外销
售时间最长不能超过多长时间? (忽略商品搬运时间及其它非
主要因素)
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
—111 — —112 — 第二章 综合测试卷
第二章 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.化简OP
→
-QP
→
+PS
→
+SP
→的结果等于 ( )
A.QP
→
B.OQ
→
C.SP
→
D.SQ
→
2.在五边形ABCDE 中(如图),AB
→
+BC
→
-DC
→
=
( )
A.AC
→
B.AD
→
C.BD
→
D.BE
→
3.已知边长为1的正方形 ABCD,设 AB
→
=a,AD
→
=b,
AC
→
=c,则|a-b+c|= ( )
A.1 B.2 C.3 D.4
4.已知a1
2
b=(1,2),a+b=(4,-10),则a= ( )
A.(-2,-2) B.(2,2)
C.(-2,2) D.(2,-2)
5.如 图 所 示,已 知 在 △ABC 中,O 是 重 心,则
AO
→
= ( )
A.BC
→
-
1
3
BA
→
B.
1
3
BC
→
-
2
3
BA
→
C.
2
3
BC
→
-
1
3
BA
→
D.BC
→
+
1
3
BA
→
6.如图所示,平行四边形 ABCD 的对角线相交于点O,E 为AO 的
中点,若DE
→
=λAB
→
+μAD
→(λ,μ∈R),则λ+μ 等于 ( )
A.1 B.-1 C.
1
2
D.-
1
2
7.已知|a|= 6,b=(m,3),且(b-a)⊥(2a+b),则向量a 在向量
b 方向上的投影数量的最大值为 ( )
A.4 B.2 C.1 D.
6
2
8.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器
的垂直弹射高度:在C 处(点C 在水平地面下方,O 为CH 与水平
地面ABO 的交点)进行该仪器的垂直弹射,水平地面上两个观察
点A,B 两地相距100米,∠BAC=60°,其中 A 到C 的距离比B
到C 的距离远40米.A 地测得该仪器在C 处的俯角为∠OAC=
15°,A 地测得最高点H 的仰角为∠HAO=30°,则该仪器的垂直
弹射高度CH 为 ( )
A.210(6+ 2) B.140 6
C.210 2 D.20(6- 2)
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.如图,已知半圆O 上有一个动点C,F 是AC 上靠近点C 的三等
分点,且OC 与BF 交于点E,则下列结论正确的是 ( )
A.AE
→
=
1
4
AB
→
+
1
2
AC
→
B.CE
→
=
1
4
AB
→
-
1
2
AC
→
C.BF
→
=
1
3
AB
→
+
2
3
BC
→
D.EF
→
=-
1
4
AB
→
+
1
6
AC
→
10.已知向量a=(3,1),b=(t,3),则下列说法正确的是 ( )
A.若a∥b,则t=3
B.若a⊥b,则t=-1
C.若a 与b 的夹角为120°,则t=0或t=-3
D.若a 与b 的夹角为锐角,则t>-1
11.已知△ABC 的内角A,B,C 所对边的长分别为a,b,c,A=
π
4
,
a=m,b=4,若满足条件的△ABC 有两个,则m 的值可以是
( )
A.2 2 B.2 3 C.3 D.4
12.在△ABC 中,角 A,B,C 的对边分别为a,b,c,若a
2=b
2+bc,
则角A 可为 ( )
A.
3π
4
B.
π
4
C.
7π
12
D.
2π
3
三、填空题:本题共4小题,每小题5分,共20分.
13.在平行四边形 ABCD 中,BE
→
=-3ED
→,AF
→
=
1
2
AC
→
+
1
2
AB
→,若
EF
→
=λAB
→
+μAD
→(λ,μ∈R),则λ+μ= .
14.已知平面向量a=(m,2),b=(2,m),且(a-b)∥a,则 m=
.
15.已知△ABC 内角A,B,C 的对边分别为a,b,c,那么当b=
时,满足条件a=1,A=30°的△ABC 有两个.(仅写出一
个b 的具体数值即可)
16.已知 A(-5,0),B(5,0),若 对 任 意 实 数t∈R,点 P 都 满 足
|AP
→
-tAB
→
|≥3,则PA
→·PB
→的最小值为 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)如图,已知空间四边形 ABCD,连接 AC,BD,E,F,G 分
别是BC,CD,DB 的中点,请化简以下式子,并在图中标出化简
结果.
(1)AB
→
+BC
→
-DC
→;
(2)AB
→
-DG
→
-CE
→
.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —113 — —114 —
18.(12分)设两个非零向量e1,e2 不共线,已知 AB
→
=2e1 +ke2,
CB
→
=e1+3e2,CD
→
=2e1-e2.
问:是否存在实数k,使得 A,B,D 三点共线,若存在,求出k 的
值;若不存在,说明理由.
19.(12分)已知a=(-2,4),b=(x,-2),其中x≠1.
(1)若a+3b 与ka-2b 平行,求实数k 的值;
(2)若a⊥b,证明:对任意实数λ,λa-b 与a+λb 垂直.
20.(12分)如图,在梯形ABCD 中,DC∥AB,DA=CB=AB=1.
(1)若DC=AC,AB
→
=a,AD
→
=b,试用a,b 表示AC
→;
(2)若 DC=2,M 是梯形所在平面内一点,求 MA
→·(2MB
→
+
MC
→)的最小值.
21.(12分)在△ABC 中,内角 A,B,C 所对的边分别为a,b,c,cosA
=
7
8
,c=3,且b≠c,若sinB=2sinA.
(1)求b 的值;
(2)求△ABC 的面积.
22.(12分)缉私船在 A 处测出某走私船在方
位角为30°(航向),距离为10海里的C 处,
并测得走私船正沿方位角150°的方向以9
海里/时的速度沿直线方向航行逃往相距
27海里的陆地 D 处,缉私船立即以v 海
里/时的速度沿直线方向前去截获.(方位
角:从某点的指北方向线起,依顺时针方向
到目标方向线之间的水平夹角)
(1)若v=21,求缉私船航行的方位角正弦值和截获走私船所需
的时间;
(2)缉私船是否有两种不同的航向均恰能成功截获走私船? 若
能,求v 的取值范围,若不能请说明理由.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
—115 — —116 — 第四章 综合测试卷
第四章 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.若cosα=
3
5
,且α 在第四象限,则tanα= ( )
A.
3
4
B.-
3
4
C.
4
3
D.-
4
3
2.已知tan(π+x)=2,则
sinx+cosx
2sinx-cosx
= ( )
A.1 B.
1
5
C.-
1
4
D.-
1
5
3.式子cos
π
12
cos
π
6
-sin
π
12
sin
π
6
的值为 ( )
A.
1
2
B.
2
2
C.1 D.
3
2
4.已知tanα=-1,则2sin
2α-3cos
2α= ( )
A.-
7
4
B.-
1
2
C.
1
2
D.
3
4
5.若sin(π-α)=-
5
3
,且α∈ π,
3π 2 ,则sin
π
2
+
α 2 = ( )
A.-
6
3
B.-
6
6
C.
6
6
D.
6
3
6.化简
cosα-cos3α
sin3α-sinα
的结果为 ( )
A.tanα B.tan2α C.
1
tanα
D.
1
tan2α
7.已知
sinx+
π 3
2sin
π
4
-
x 2 sin
π
4
+
x 2
=
3 3
4
,则tanx 的值为 ( )
A.-
3
2
B.
3
2
C.-
3
8
D.
3
8
8.已知sin
7π
6 +α =
3
3
,则cos
2π
3 -2α = ( )
A.-
2
3
B.-
1
3
C.
2
3
D.
1
3
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.函数f(x)=sinxcosx 的单调递减区间可以是 ( )
A.kπ3π
4
,kππ
4
?
?
??
?
?
??
(k∈Z)
B.kπ+
π
4
,kπ+
3π
4
?
?
??
?
?
??
(k∈Z)
C.2kπ+
π
4
,2kπ+
π
2
?
?
??
?
?
??
(k∈Z)
D.kπ+
π
4
,kπ+
π
2
?
?
??
?
?
??
(k∈Z)
10.以下命题是假命题的是 ( )
A.存在x∈R,使得sin
2 x
2
+cos
2 x
2
=
1
2
B.存在x,y∈R,使得sin(x-y)=sinx-siny
C.对于任意的x∈[0,π],都有
1-cos2x
2
=sinx
D.sinx=cosy⇒x+y=
π
2
11.已知θ∈(0,π),sinθ+cosθ=
1
5
,则下列结论正确的是 ( )
A.θ∈
π
2 ,π B.cosθ=-
3
5
C.tanθ=-
3
4
D.sinθ-cosθ=
7
5
12.已知函数f(x)=sin
2x+2 3sinxcosx-cos
2x,x∈R,则( )
A.-2≤f(x)≤2
B.f(x)在区间(0,π)上只有1个零点
C.f(x)的最小正周期为π
D.x=
2π
3
为f(x)图象的一条对称轴
三、填空题:本题共4小题,每小题5分,共20分.
13.已知θ∈
π
2 ,π ,若sinθ+
3π 2 =
4
5
,则cos
θ
2
= .
14.已知tanα,tanβ 是 一 元 二 次 方 程x
2 +3x-4=0 的 2 个 根,
cos2α+cos2β
sin2α+sin2β
= .
15.已知sin
π
8 -α =
1
3
,则sin2α+cos2α= .
16.将函数y=3cos2x+
π 6 的图象向右平行移动
π
6
个单位长度得
到函数y=f(x)的图象,若f(α)= 2,则f 2απ 12 =
.
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)已知2sinα+cosα=0.
(1)求tanα;
(2)求
sin
2α+2cos
2α
3sinαcosα
的值.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —117 — —118 —
18.(12分)如图,在四边形ABCD 中,A 为锐角,
且2cosAsin(A+C)= 3sinCπ 6 ,求A+C
的值.
19.(12分)在△ABC 中,求 2sinA+sinBsinC 的最大值.
20.(12分)已知函数f(x)=sin
x
2
cos
x
2
- 3cos
2 x
2
+
3
2
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)在 △ABC 中,角 A,B,C 所 对 的 边 分 别 是a,b,c,且 满 足
c
2-b
2≥ 3ac-a
2,求f(B)的取值范围.
21.(12分)已知函数f(x)=2sinxcosx+2 3sinx+
π 4 cos x+
π
4 .
(1)求函数f(x)的对称轴方程;
(2)将函数f(x)的图象向右平移
π
3
个单位长度,得到函数g(x)
的图象,当x∈ 0,
π
2
?
?
??
?
?
??
时,求g(x)的值域.
22.(12 分)已 知 向 量 a= (sinx,-1),b= 3cosx,-
1 2 ,函 数
f(x)=(a+b)·a-2.
(1)求函数f(x)的最小正周期T;
(2)若x∈ 0,
π
2
?
?
??
?
?
??
,求函数f(x)的值域.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
—119 — —120 — 第五章 综合测试卷
第五章 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.复数1-2i的虚部为 ( )
A.-2i B.2i C.-2 D.2
2.若复数z=1-2i,其中i是虚数单位,则z 对应的点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.复数z 满足|z-2|=1,则|z|的最大值为 ( )
A.1 B.2 C.3 D.3
4.已知复数z 对应的向量为OZ
→(O 为坐标原点),OZ
→与实轴正向的
夹角为120°,且复数z 的模为2,则复数z 为 ( )
A.1+ 3i B.2
C.1- 3i D.-1+ 3i
5.若复数z 满足2z-z?=1+3i,则z= ( )
A.1+i B.1-i
C.-1+i D.-1-i
6.已知i为虚数单位,设z=5+3i,则在复平面内,复数z-5i所对
应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.已知z?是复数z 的共轭复数,若z(1+i)=2-i,则z?的虚部为
( )
A.-
1
2
B.
1
2
C.-
3
2
D.
3
2
8.已知复数3-2i是关于x 的方程2x
2-mx+n=0的一个根,则实
数m,n 的值分别为 ( )
A.6,5 B.12,10 C.12,26 D.24,26
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.设复数z 满足z=-1-2i,i为虚数单位,则下列命题正确的是
( )
A.|z|= 5
B.复数z 在复平面内对应的点在第四象限
C.z 的共轭复数为-1+2i
D.复数z 在复平面内对应的点在直线y=-2x 上
10.设z1,z2 是复数,则下列命题中的真命题是 ( )
A.|z1-z2|=0,则z1=z2
B.若z1=z2,则z1=z2
C.若|z1|=|z2|,则z1·z1=z2·z2
D.若|z1|=|z2|,则z1=±z2
11.若复数z 满足(1+i)z=3-i ( )
A.z 的实部为1 B.z 的虚部为-4
C.z?=1-2i D.|z|= 5
12.已知i为虚数单位,则下列结论正确的是 ( )
A.若复数z1,z2 互为共轭复数,则z1·z2 为实数
B.若复数z1,z2 满足|z1|=|z2|,则z1,z2 互为共轭复数
C.若复数z 满足
1
z
∈R,则z∈R
D.对任意的复数z,都有z
2≥0
三、填空题:本题共4小题,每小题5分,共20分.
13.若复数z=m
2 -1+(m
2 -m -2)i为纯虚数,则实数 m 的值
为 .
14.设z1=|a|+bi,z2=1+bi(a,b∈R),若z1<z2,则a,b 应满足
的条件是 .
15.设复数z=a+bi(a,b∈R,i是虚数单位),若z+2z?=3+2i,则
a= ,b= .
16.设复数z满足(1-i)z=1+2i(i是虚数单位),则|z|= ,
z 的虚部为 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)已知复数z=m
2+m-(m+1)i,m∈R,i为虚数单位.
(1)当z 是纯虚数时,求m 的值;
(2)当m=1时,求z 的值.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —121 — —122 —
18.(12分)实数 m 分别为何值时,复数z=
2m
2+m-3
m+3
+(m
2 -
3m-18)i是
(1)实数;
(2)虚数;
(3)纯虚数.
19.(12分)已知复数z=x+yi(x,y∈R),且|z-2|= 2,求
y+2
x
的最大值.
20.(12分)已知复数z 在复平面内对应的点在第四象限,|z|=1,且
z+z?=1,求z.
21.(12分)已知复数z1=1+3i,z2=2+2i.
(1)求z1z2,及|z1+z2|;
(2)在复平面上,复数z1,z2 分别对应的点为A,B,求A,B 两点
间的距离.
22.(12分)已知复数z=
1
4
-a+
3
2
i(a∈R,a>0),且
1
z
+z∈R.
(1)求复数z 及|z|;
(2)若复数(z+m)2(m∈R)在复平面内对应的点在第四象限,求
m 的取值范围.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
—123 — —124 — 第六章 综合测试卷
第六章 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.如图所示,观察四个几何体,其中判断正确的是 ( )
A.①是棱台 B.②是圆台
C.③是棱锥 D.④是棱柱
2.如图,在△ABC 中,BC=4,AB=AC=2 5,若△ABC 的水平放
置直观图为△A'B'C',则△A'B'C'的面积为 ( )
A.2 B.2 2 C.3 2 D.4 2
3.以下命题正确的是 ( )
A.过空间三点有且仅有一个平面
B.平行于同一直线的两个平面互相平行
C.平行于同一直线的两条直线互相平行
D.分别在两个平行平面内的两条直线互相平行
4.如图所示,在正方体 ABCD-A1B1C1D1 中,与
平面AB1C 平行的直线是 ( )
A.DD1 B.A1D1
C.C1D1 D.A1D
5.如图,在棱长为2的正方体 ABCD-A1B1C1D1 中,E,F,G 分别
为A1D1,A1B1,BB1 的中点,过E,F,G 三点的
平面截正方体 ABCD-A1B1C1D1 所得的截面
面积为 ( )
A.4 B.4 2
C.
3 3
2
D.3 3
6.已知三棱锥P-ABC 中,PA⊥底面ABC,底面ABC 是边长为2的
正三角形,PA=4,则三棱锥P-ABC 的外接球表面积为 ( )
A.
32 3π
27
B.
64π
3
C.
32π
3
D.
64π
27
7.已知圆锥SO 的底面半径为r,当圆锥的体积为
2
6
πr
3 时,该圆锥
的母线与底面所成角的正弦值为 ( )
A.
3
3
B.
2
3
C.
3
2
D.
2
2
8.已知四边形ABCD 是边长为4的正方形,E,F 分别是边AB,AD
的中点,GC 垂直于正方形ABCD 所在平面α,且GC=2,则点 B
到平面EFG 的距离为 ( )
A.3 B.5 C.
11
11
D.
2 11
11
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.在正四面体PABC 中,D,E,F 分别是AB,BC,CA 的中点,下面
结论中正确的是 ( )
A.BC∥平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
10.如 图,正 方 体 ABCD -A1B1C1D1 中,若
E,F,G 分 别 为 棱 BC,CC1,B1C1 的 中
点,O1,O2 分 别 是 四 边 形 ADD1A1,
A1B1C1D1 的中心,则 ( )
A.A,C,O1,D1 四点共面
B.D,E,G,F 四点共面
C.A,E,F,D1 四点共面
D.G,E,O1,O2 四点共面
11.在三棱锥A-BCD 中,AB⊥平面BCD,BC⊥CD,AB=BC=1,
BD= 2,三棱锥 A-BCD 的所有顶点均在球O 的表面上,若点
M,N 分别为△BCD 与△ABD 的重心,直线 MN 与球O 的表
面相交于F,G 两点,则 ( )
A.三棱锥A-BCD 的外接球表面积为3π
B.点O 到线段MN 的距离为
3
3
C.|FG|=
2 6
3
D.|FG|∶|MN|=2 3
12.如图,四棱锥 P-ABCD 的底面为矩形,PD
⊥底面ABCD,AD=1,PD=AB=2,点E
是PB 的中点,过 A,D,E 三点的平面α 与
平面PBC 的交线为l,则 ( )
A.l∥平面PAD
B.AE∥平面PCD
C.直线PA 与l所成角的余弦值为
5
5
D.平面α 截四棱锥P-ABCD 所得的上、下两部分几何体的体积
之比为
3
5
三、填空题:本题共4小题,每小题5分,共20分.
13.如图,四棱锥S-ABCD 的所有棱长都等于
2,E 是SA 的中点,过C,D,E 三点的平面
与SB 交于点F,则四边形 DEFC 的周长为
.
14.若一个直三棱柱的所有棱长都为1,且其顶
点都在一个球面上,则该球的表面积为 .
15.已知三棱锥P-ABC 的所有棱长为2,D,E,F 分别为PA,PB,
PC 的中点,则此三棱锥的外接球被平面 DEF 所截的截面面积
为 .
16.已知四棱锥P-ABCD 的底面ABCD 是边长为4的正方形,PD
⊥平面 ABCD,PD =6,E 为棱PD 上一点,且 ED =2PE,过
EB 作平面α 分别与线段PA,PC 交于点 M,N,且 AC∥α,则
PM
PA
= ,四边形EMBN 的面积为 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)已知某一圆柱体内接于球O,若该圆柱体的高h=8,且
球O 的表面积为100π.
(1)求该圆柱体的表面积S;
(2)设该圆柱体的体积为V1,球O 的体积为V2,求
V1
V2
.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —125 — —126 —
18.(12分)如图,已知四面体 ABCD 中,E,F,G,H 分别是边AB,
BC,CD,DA 上 的 点 (与 端 点 不 重 合),BD∥平 面 EFGH,且
EH =FG.
(1)求证:EH∥FG;
(2)求证:HG∥平面ABC.
19.(12分)如图,在三棱柱ABC-A1B1C1 中,F 为AC 中点.
(1)求证:AB1∥平面BFC1;
(2)若此三棱柱为正三梭柱,且 A1A = 2A1C1,求 ∠FBC1 的
大小.
20.(12分)如图所示,在正方体 ABCD-A1B1C1D1 中,E,F,G,H
分别是BC,CC1,C1D1,A1A 的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D;
(3)平面BDF∥平面B1D1H .
21.(12 分)如 图 所 示,四 棱 锥 P-ABCD 的 底 面 ABCD 是 矩 形,
PA=PB=AB=4,BC=2 2,PC=2 6,点 E 为AB 的中点,
AC 与BD 交于点O.
(1)求证:PE⊥平面ABCD;
(2)求三棱锥D-PAE 的体积.
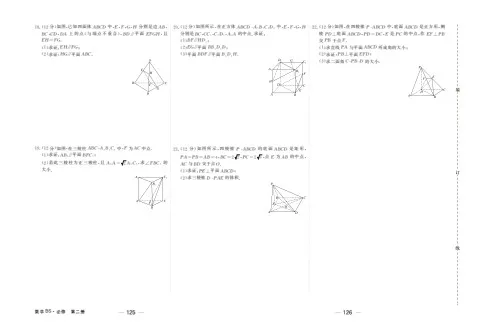
22.(12分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是正方形,侧
棱PD⊥底面 ABCD,PD=DC,E 是PC 的中点,作 EF⊥PB
交PB 于点F.
(1)求直线PA 与平面ABCD 所成角的大小;
(2)求证:PB⊥平面EFD;
(3)求二面角C-PB-D 的大小.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
—127 — —128 — 必修第二册 综合测试卷
必修第二册 综合测试卷
时间:120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四
个选项中,只有一项是符合题目要求的.
1.复数
2
1-i
(i为虚数单位)的共轭复数是 ( )
A.1+i B.1-i C.-1+i D.-1-i
2.如图,向量 AB
→
=a,AC
→
=b,CD
→
=c,则向量
BD
→可以表示为 ( )
A.a+b-c B.a-b+c
C.b-a+c D.b-a-c
3.如果角α 的终边过点P(2sin30°,-2cos30°),则sinα 的值等于
( )
A.
1
2
B.-
1
2
C.-
3
2
D.-
3
3
4.在△ABC 中,内角 A,B,C 所对的边分别为a,b,c,其中a=3,
c=2 3,bsinA=acosB+
π 6 ,则b= ( )
A.1 B.2 C.3 D.5
5.已知直三棱柱 ABC-A1B1C1 中,∠ABC=120°,AB =2,BC=
CC1=1,则异面直线AB1 与BC1 所成角的余弦值为 ( )
A.
3
2
B.
15
5
C.
10
5
D.
3
3
6.若3cos
π
2 -θ +cos(π+θ)=0,则cos
2θ+
1
2
sin2θ的值是 ( )
A.-
6
5
B.-
4
5
C.
6
5
D.
4
5
7.如图,已知等边△ABC 与等边△ABD 所在平
面成锐二面角
π
3
,E,F 分别为AB,AD 的中
点,则异面直线EF 与CD 所成角的余弦值为
( )
A.
2 3
3
B.
3
2
C.
3
4
D.
4 3
3
8.函数f(x)=Asin(ωx+φ) A>0,ω>0,|φ|<
π
2 的部分图象如图所示,将函数f(x)的图象
向左平移
π
3
个单位长度后得到y=g(x)的 图
象,则下列说法正确的是 ( )
A.函数g(x)为奇函数
B.函数g(x)的最小正周期为2π
C.函数g(x)的图象的对称轴为直线x=kπ+
π
6
(k∈Z)
D.函数g(x)的单调递增区间为 -
5π
12
+kπ,
π
12
+kπ
?
?
??
?
?
??
(k∈Z)
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选
项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,
有选错的得0分.
9.在△ABC 中,内角A,B,C 所对的边分别为a,b,c,若a=1,b=
3,A=30°,则B= ( )
A.30° B.150° C.60° D.120°
10.若将函数f(x)=cos2x+
π 12 的图象向左平移
π
8
个单位长度,
得到函数g(x)的图象,则下列说法正确的是 ( )
A.g(x)的最小正周期为π
B.g(x)在区间 0,
π
2
?
?
??
?
?
??
上单调递减
C.x=
π
12
是函数g(x)的对称轴
D.g(x)在 -
π
6
,
π
6
?
?
??
?
?
??
上的最小值为1
2
11.如图是一几何体的平面展开图,其中四边形
ABCD 为正方形,E,F,G,H 分别为PA,
PD,PC,PB 的中点.在此几何体中,给出
下列结论,其中正确的结论是 ( )
A.平面EFGH∥平面ABCD
B.直线PA∥平面BDG
C.直线EF∥平面PBC
D.直线EF∥平面BDG
12.在矩形ABCD 中,AB=4,BC=3,沿矩形对角线BD 将△BCD
折起形成四面体ABCD,在这个过程中,现在下面四个结论其中
所有正确结论为 ( )
A.在四面体ABCD 中,当DA⊥BC 时,BC⊥AC
B.四面体ABCD 的体积的最大值为
24
5
C.在四面体ABCD 中,BC 与平面ABD 所成角可能为
π
3
D.四面体ABCD 的外接球的体积为定值
三、填空题:本题共4小题,每小题5分,共20分.
13.已知向量a=(m,1),b=(1,-2),c=(2,3),若a-b 与c 共线,
则实数m= .
14.复数6+5i与-3+4i分别表示向量OA
→与OB
→,则表示向量BA
→
的复数为 .
15.在正三棱锥S-ABC 中,AB=BC=CA=6,点D 是SA 的中点,
若SB⊥CD,则该三棱锥外接球的表面积为 .
16.已知函数f(x)=sin(ωx+φ)ω>0,0<φ<
π 2 的图象既关于点
π
4 ,0 对称,又关于直线x=-
π
4
对称,最小正周期 T∈
π
2 ,π ,
则T= ,f(x)的单调递减区间是 .
四、解答题:本题共6小题,共70分,解答应写出文字说明、证明过程
或演算步骤.
17.(10分)已知点A(-3,-4),B(5,-12).
(1)求AB
→的坐标及|AB
→
|;
(2)若OC
→
=OA
→
+OB
→,OD
→
=OA
→
-OB
→,求OC
→及OD
→的坐标;
(3)求OA
→·OB
→
.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
数学BS·必修 第二册 —129 — —130 —
18.(12分)△ABC 的内角A,B,C 的对边分别为a,b,c,已知sin(A
+C)=8sin
2 B
2
.
(1)求cosB;
(2)若a+c=6,△ABC 面积为2,求b.
19.(12分)已知函数f(x)=2cosx(sinx- 3cosx)+ 3.
(1)求f(x)的最小正周期和f(x)的单调递减区间;
(2)当x∈
π
2
,π
?
?
??
?
?
??
时,求函数f(x)的最小值及取得最小值时x
的值.
20.(12分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是矩形,E,F
分别是棱PC 和PD 的中点.
(1)求证:EF∥平面PAB;
(2)若AP=AD,且平面 PAD ⊥平面 ABCD,求证:AF⊥平面
PCD.
21.(12分)如图所示,在直三棱柱 ABC-A1B1C1 中,AC=3,BC=
4,AB=5,AA1=4,D 是AB 的中点.
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求三棱锥C1-CDB1 的体积.
22.(12分)如图,在三棱锥 P-ABC 中,PB⊥平面 ABC,△ABC 是
直角三角形,∠B=90°,AB=BC=2,∠PAB=45°,D,E,F 分
别为AC,AB,BC 的中点.
(1)求证:EF⊥PD;
(2)求直线PF 与平面PBD 所成的角的正弦值;
(3)求二面角E-PF-B 的正切值.
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
















 该页无缩略图
该页无缩略图



