密

封

线

学

校 ______________________班

级 ______________________姓

名 ______________________考

号 ______________________

◆

全

优

课

堂·数

学·九

年

级

上

册

一、选择题（每小题 4 分，共 48 分）

1. 下列方程为一元二次方程的是 （ ）

A． x-2=0 B． x2

-2x-3

C． x2

-4x+1=0 D． y=x2

-1

2. 若关于 x 的一元二次方程 x2

-ax=0 的一个解是-1，则 a 的值为 （ ）

A． 1 B． -2 C． -1 D． 2

3. 关于 x 的一元二次方程 x2

+ax-1=0 的根的情况是 （ ）

A． 没有实数根 B． 只有一个实数根

C． 有两个相等的实数根 D． 有两个不相等的实数根

4. 用配方法解方程 x2

+10x+9=0，配方后可得 （ ）

A．（x+5）2

=16 B．（x+5）2

=1

C．（x+10）2

=91 D．（x+10）2

=109

5. 定义运算：a★b=a（1-b）．若 a，b 是方程 x2

-x+ 1

4 m=0（m＜0）的两根，则 b★b-a★a 的

值为 （ ）

A． 0 B． 1 C． 2 D． 与 m 有关

6.（新点）若关于 x 的一元二次方程 ax2

+bx+c＝0（ac≠0）有一根为 x＝2 019，则关于 y

的一元二次方程 cy2

+by+a＝0（ac≠0）必有一根为 （ ）

A． 1

2 019 B． - 1

2 019 C． 2 019 D． -2 019

7. 若关于 x 的一元二次方程 x2

-（k+3）x+2k+2＝0 有一根小于 1，一根大于 1，则 k 的

取值范围是 （ ）

A． k≠1 B． k＜0 C． k＜-1 D． k＞0

8. 若 x=x0 是方程 ax2

+2x+c=0（a≠0）的一个根，设 M=1-ac，N=（ax0+1）2

，则 M 与 N

的大小关系正确的为 （ ）

A． M＞N B． M=N C． M＜N D． 不确定

9. 关于 x 的一元二次方程（a-1）x2

-2x+3=0 没有实数根，则整数 a 的最小值是（ ）

A． 0 B． 1

C． 2 D． 3

10. 已知关于 x 的一元二次方程 x2

+x-m+ 9

4 =0 有两个不相等的实数根，则实数 m 的

取值范围是 （ ）

A． m＜2 B． m＜-2

C． m＞-2 D． m＞2

11. 某型号手机连续两次降价，每台手机售价由原来的 1 185 元降到 580 元，设平

均每次降价的百分率为 x，则列出方程正确的是 （ ）

A． 580（1+x）2

＝1 185 B． 1 185（1-x）2

＝580

C． 580（1-x）2

＝1 185 D． 1 185（1+x）2

＝580

12. 如图，某工厂师傅要在一个面积为 15 m2 的矩形钢板上裁剪下两个相邻的正方形

钢板当工作台的桌面，且要使大正方形的边长比小正方形的边长大 1 m，则裁剪

后剩下的阴影部分的面积为 （ ）

A. 8 m2 B. 4 m2

C. 2 m2 D. 1 m2

（第 12 题图）

二、填空题（每空 4 分，共 16 分）

13. 方程 x（x-5）＝2x 的根是 ________.

14.（易错点）已知关于 x 的一元二次方程（k-2）2

x2

+（2k+1）x+1=0 有两个不相等的实

数根，则偶数 k 的最小取值为 _______.

15.（模型观念）水果店老板以每斤 2 元的价格购进某种水果若干斤，然后以每斤 4 元

的价格出售，每天可售出 100 斤，通过调查发现，这种水果每斤的售价每降低 0.1

元，每天可多售出 20 斤，为保证每天至少售出 260 斤，老板决定降价销售．

（1）若这种水果每斤售价降低 x 元，则每天的销售量是 _______ 斤（用含 x 的代

数式表示，需要化简）；

（2）销售这种水果要想每天盈利 300 元，老板需将每斤的售价定为 ____ 元.

题 号 一 二 总 分

分 值

三

第二十一章高频考题组合卷

（时间：90 分钟 满分：１2０ 分）

133 134

三、解答题（共 56 分）

16.（12 分）解下列方程：

（1）2（x-2）2

=18； （2）5x2

+5x=-1-x；

（3）x2

+4x+2=0； （4）（x-2）（x+3）=2x+6．

17.（10 分）关于 x 的一元二次方程 x2

+（2k+1）x+k2

+1=0 有两个不相等实数根 x1，x2．

（1）求实数 k 的取值范围；

（2）若方程的两实根 x1，x2 满足 x1+x2=-x1x2，求 k 的值．

18.（模型观念）（10 分）果农李明种植的草莓计划以每千克 15 元的单价对外批发销

售，由于部分果农盲目扩大种植，造成该草莓滞销．李明为了加快销售，减少损

失，对价格进行两次下调后，以每千克 9.6 元的单价对外批发销售．

（1）求李明平均每次下调的百分率；

（2）小刘准备到李明处购买 3 t 该草莓，因数量多，李明决定再给予两种优惠方

案供其选择：

方案一：打九折销售；方案二：不打折，每吨优惠现金 400 元．

试问小刘选择哪种方案更优惠，请说明理由．

19.（12 分）如图所示，利用 22 m 长的墙为一边，用篱笆围成一个矩形养鸡场，中间

用篱笆分割出两个小矩形，总共用去篱笆 36 m，为了使这个矩形 ABCD 的面积

为 96 m2

，问 AB 和 BC 各应是多少？

A

F

E

B

D

C

（第 19 题图）

20.（12 分）某青年旅社有 60 间客房供游客居住，在旅游旺季，当客房的定价为每

天 200 元时，所有客房都可以住满．客房定价每提高 10 元，就会有 1 间客房空

闲，对有游客入住的客房，旅社还需要对每个房间支出 20 元/天的维护费用，设

每间客房的定价提高了 x 元．

（1）填表（不需化简）：

入住的房间数量（间） 房间价格（元） 总维护费用（元）

提价前 60 200 60×20

提价后 ___________ ___________ ___________

（2）若该青年旅社希望每天纯收入 14 000 元且能吸引更多的游客，则每间客房

的定价应为多少元？（纯收入=总收入-总维护费用）

135 136

密

封

线

学

校 ______________________班

级 ______________________姓

名 ______________________考

号 ______________________

◆

全

优

课

堂·数

学·九

年

级

上

册

一、选择题（每小题 4 分，共 40 分）

1. 下列各式中，y 是 x 的二次函数的是 （ ）

A． y= 1

x2 B． y=2x+1 C． y=x2

+x-2 D． y2

=x2

+3x

2. 抛物线 y=（x-1）2 的顶点在 （ ）

A． 原点 B． x 轴上 C． y 轴上 D． 第一象限

3. 若二次函数 y=ax2

+bx+a2

-3（a，b 为常数）的图象，如图，则 a 的值为 （ ）

A． 1 B． 姨3 C． -姨3 D． -3

O

y

x

1

y

O x

（第 3 题图） （第 5 题图）

4. 要得到抛物线 y=2（x-4）2

-1，可以将抛物线 y=2x2 （ ）

A． 向左平移 4 个单位长度，再向上平移 1 个单位长度

B． 向左平移 4 个单位长度，再向下平移 1 个单位长度

C． 向右平移 4 个单位长度，再向上平移 1 个单位长度

D． 向右平移 4 个单位长度，再向下平移 1 个单位长度

5. 已知抛物线 y=ax2

+bx+1 的大致位置如图所示，那么直线 y=ax+b 不经过 （ ）

A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限

6.（重点）已知（1，y1），（-2，y2），（-4，y3）都是抛物线 y=-2ax2

+8ax+3（a＜0）上的点，则

下列各式中正确的是 （ ）

A． y1＜y3＜y2 B． y3＜y2＜y1

C． y2＜y3＜y1 D． y1＜y2＜y3

7. 心理学家发现：学生对概念的接受能力 y 与提出概念的时间 x（min）之间是二次

函数关系，当提出概念 13 min 时，学生对概念的接受力最大，为 59.9；当提出概

念 30 min 时，学生对概念的接受能力就剩下 31，则 y 与 x 满足的二次函数关系

式为 （ ）

A． y=-（x-13）2

+59.9 B． y=-0.1x2

+2.6x+31

C． y=0.1x2

-2.6x+76.8 D． y=-0.1x2

+2.6x+43

8. 如图，二次函数 y=ax2

+bx+c（a＞0）的图象与直线 y=1 的交点坐标为（1，1），（3，1），

则不等式 ax2

+bx+c-1＞0 的解集为 （ ）

A． x＞1 B． 1＜x＜3 C． x＜1 或 x＞3 D． x＞3

1 2 3 4 5

5

4

3

2

1

-1

y

O x

-1 O 1

y

x

O

C

B

A

y

x

（第 8 题图） （第 10 题图） （第 14 题图）

9.（难点）已知二次函数 y=（x-h）2

+1（h 为常数），在自变量 x 的值满足 1≤x≤3 的情况

下，与其对应的函数值 y 的最小值为 5，则 h 的值为 （ ）

A． 1 或-5 B． -1 或 5 C． 1 或-3 D． 1 或 3

10. 如图，已知二次函数 y=ax2

+bx+c（a≠0）的图象如图所示，有下列 5 个结论：

①abc＜0；②b＜a+c；③4a+2b+c＞0；④2c＜3b；⑤a+b＜m（am+b）（m≠1 的实数）．其中正

确的结论有 （ ）

A． ①②③ B． ①③④ C． ③④⑤ D． ②③⑤

二、填空题（每小题 4 分，共 16 分）

11.（易错点）若二次函数 y=（m-姨2 ）x2

+2x+（m2

-2）的图象经过原点，则 m=_______．

12. 如果二次函数 y=ax2

+bx 的图象与 x 轴交于点 A（-1，0），B（3，0），那么方程 ax2

+

bx=0 的根是 _________．

13. 某厂今年一月份新产品的研发资金为 1 000 元，以后每月新产品的研发资金与

上月相比增长率都是 x，则该厂今年三月份新产品的研发资金 y（元）关于 x 的函数关

系式为________________．

14. 如图，四边形 OABC 是边长为 1 的正方形，OC 与 x 轴正半轴的夹角为 15°，点 B

在抛物线 y=ax（2 a＜0）的图象上，则 a 的值为 _________．

题 号 一 二 三 总 分

分 值

137 138

第二十二章高频考题组合卷

（时间：90 分钟 满分：１2０ 分）

三、解答题（共 64 分）

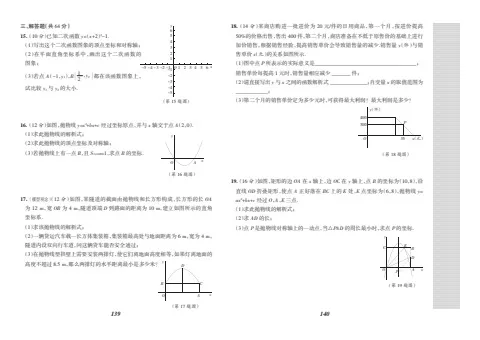
15.（10 分）已知二次函数 y=（x+2）2

-1.

（1）写出这个二次函数图象的顶点坐标和对称轴；

（2）在平面直角坐标系中，画出这个二次函数的

图象；

（3）若点 A（-1，y1），B 1

2

2 ，y2 \"都在该函数图象上，

试比较 y1 与 y2 的大小．

16.（12 分）如图，抛物线 y=x2

+bx+c 经过坐标原点，并与 x 轴交于点 A（2，0）．

（1）求此抛物线的解析式；

（2）求此抛物线的顶点坐标及对称轴；

（3）若抛物线上有一点 B，且 S△OAB=1，求点 B 的坐标．

17.（模型观念）（12 分）如图，某隧道的截面由抛物线和长方形构成，长方形的长 OA

为 12 m，宽 OB 为 4 m，隧道顶端 D 到路面的距离为 10 m，建立如图所示的直角

坐标系.

（1）求该抛物线的解析式；

（2）一辆货运汽车载一长方体集装箱，集装箱最高处与地面距离为 6 m，宽为 4 m，

隧道内设双向行车道，问这辆货车能否安全通过；

（3）在抛物线型拱壁上需要安装两排灯，使它们离地面高度相等，如果灯离地面的

高度不超过 8.5 m，那么两排灯的水平距离最小是多少米？

18.（14 分）某商店购进一批进价为 20 元/件的日用商品，第一个月，按进价提高

50%的价格出售，售出 400 件，第二个月，商店准备在不低于原售价的基础上进行

加价销售，根据销售经验，提高销售单价会导致销售量的减少．销售量 y（件）与销

售单价 x（元）的关系如图所示．

（1）图中点 P 所表示的实际意义是______________________________________；

销售单价每提高 1 元时，销售量相应减少 _______ 件；

（2）请直接写出 y 与 x 之间的函数解析式 ______________；自变量 x 的取值范围为

____________；

（3）第二个月的销售单价定为多少元时，可获得最大利润？ 最大利润是多少？

35

400

300

O

y（件）

x（元）

P

（第 18 题图）

19.（16 分）如图，矩形的边 OA 在 x 轴上，边 OC 在 y 轴上，点 B 的坐标为（10，8），沿

直线 OD 折叠矩形，使点 A 正好落在 BC 上的 E 处，E 点坐标为（6，8），抛物线 y=

ax2

+bx+c 经过 O，A，E 三点．

（1）求此抛物线的解析式；

（2）求 AD 的长；

（3）点 P 是抛物线对称轴上的一动点，当△PAD 的周长最小时，求点 P 的坐标．

y

A

C B

O x P

D

E

（第 19 题图）

y

O A x

（第 16 题图）

139 140

（第 15 题图）

-5 -4 -3 -2 -1 1 2 3 4 5 6

6

5

4

3

2

1

-1

-2

-3

-4

-5

y

O x

y

O x

B

D

C

A

（第 17 题图）

密

封

线

学

校 ______________________班

级 ______________________姓

名 ______________________考

号 ______________________

◆

全

优

课

堂·数

学·九

年

级

上

册

一、选择题（每小题 4 分，共 40 分）

1. 下列图形中是中心对称图形的是 （ ）

A B C D

2.（几何直观）如图，沿图中的右边缘所在的直线为轴将该图形向右翻折 180°后，再

将翻折后的正方形绕它的右下顶点按顺时针方向旋转 90°，所得到的图形是

（ ）

（第 2 题图） A B C D

3. 如图，将一个含 30°角的直角三角板 ABC 绕点 A 顺时针旋转，使得点 B，A，C′

在同一条直线上，则三角板 ABC 旋转的角度是 （ ）

A． 60° B． 90° C． 120° D． 150°

30°

B A C′

C B′ C

O

B

A

C′

A′

B′

y

x

A

E C

F

B

（第 3 题图） （第 5 题图） （第 6 题图）

4. 若点 P（-m，m-3）关于原点对称的点是第二象限内的点，则 m 满足 （ ）

A． m＞3 B． 0＜m≤3 C． m＜0 D． m＜0 或 m＞3

5.（易错点）如图，将△ABC 绕点 P 顺时针旋转 90°得到△A′B′C′，则点 P 的坐标是

（ ）

A．（1，1） B．（1，2） C．（1，3） D．（1，4）

6. 如图，△ABC 中，AB=AC，△ABC 与△FEC 关于点 C 成中心对称，连接 AE，BF，

当∠ACB 为 _____ 度时，四边形 ABFE 为矩形 （ ）

A． 90 B． 30 C． 60 D． 45

7. 如图，△ABC 是等腰直角三角形，BC 是斜边，P 为△ABC 内一点，将△ABP 逆时

针旋转后，与△ACP′重合，如果 AP=4，那么 P，P′两点间的距离为 （ ）

A． 4 B． 4姨2 C． 4姨3 D． 8

A

B

P

P′

C D A

C B

B′

D′ C′ A

F

B E D C

（第 7 题图） （第 8 题图） （第 10 题图）

8. 如图，把矩形 ABCD 绕点 A 顺时针旋转，使点 B 的对应点 B′落在 DA 的延长线

上，若 AB=2，BC=4，则点 C 与其对应点 C′的距离为 （ ）

A． 6 B． 8 C． 2姨5 D． 2姨10

9. 在平面直角坐标系中，点 P（1，-2）向右平移 2 个单位长度得到点 P1，点 P1 绕原

点逆时针旋转 90°得到点 P2，则点 P2 的坐标是 （ ）

A．（-2，-3） B．（2，-3） C．（-2，3） D．（2，3）

10.（重点）如图，在 Rt△ABC 中，AB=AC，D，E 是斜边 BC 上两点，且∠DAE=45°，将

△ADC 绕点 A 顺时针旋转 90°后，得到△AFB，连接 EF，下列结论：①BF⊥BC；

②△AED≌△AEF；③BE+DC=DE；④BE2

+DC2

=DE2

，其中正确的个数是 （ ）

A． 1 B． 2 C． 3 D． 4

二、填空题（每小题 4 分，共 12 分）

11. 如图，△ABC 中，∠C=30°．将△ABC 绕点 A 顺时针旋转 60°得到△ADE，AE 与

BC 交于 F，则∠AFB=_____°．

E

F B

D

C A

A E

D

C B

（第 11 题图） （第 12 题图）

12. 如图，在△ABC 中，∠ACB=90°，BC=2，将△ACB 绕点 C 逆时针旋转 60°得到

△DCE（A 和 D，B 和 E 分别是对应顶点），若 AE∥BC，则△ADE 的周长为 _____．

题 号 一 总 分

分 值

二 三

141 142

第二十三章高频考题组合卷

（时间：90 分钟 满分：１2０ 分）

13．（难点）如图，O 为坐标原点，矩形 OABC 中，A（-8，0），C（0，6），将

矩形 OABC 绕点 O 旋转 60°，得到矩形 OA′B′C′，此时直线 OA′

与直线 BC 相交于 P．则点 P 的坐标为 ___________________.

三、解答题（共 68 分）

14.（8 分）如图，在 Rt△ABC 中，∠B=90°，AB=BC，A，B 的坐标

分别为（0，4），（-2，4），将△ABC 绕点 P 旋转 180°后得到△A′B′C′，其中点 B 的

对应点 B′的坐标为（2，2）．

（1）求出点 C 的坐标；

（2）求点 P 的坐标，并求出点 C 的对应点 C′的坐标．

15.（10 分）如图，四边形 ABCD 是正方形，△ADF 旋转一定角度后得到△ABE，

如果 AF=4，AB=7.

（1）指出旋转中心和旋转角度；

（2）求 DE 的长度；

（3）BE 与 DF 的位置关系如何？ 并说明理由．

16.（10 分）如图，在 Rt△ABC 中，∠ACB=90°，点 D，E 分别在 AB，AC 上，CE=BC，

连接 CD，将线段 CD 绕点 C 按顺时针方向旋转 90°后得 CF，连接 EF．

（1）补充完成图形；

（2）若 EF∥CD，求证：∠BDC=90°．

17.（12 分）现有如图 1 所示的两种瓷砖．请从这两种瓷砖中各选 2 块，拼成一个新

的正方形地板图案，使拼铺的图案成轴对称图形或中心对称图形（如图 2）．

图 1 图 2 图 3 图 4

（第 17 题图）

18.（13 分）如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为

A（-3，5），B（-2，1），C（-1，3）．

（1）若 △ABC 经 过 平 移 后 得 到 △A1B1C1， 已 知 点 C1 的 坐 标 为（4，0）， 画 出

△A1B1C1，并写出顶点 A1，B1 的坐标；

（2）若△ABC 和△A2B2C2 关于原点 O 成中心对称图形，写出△A2B2C2 的各顶点的

坐标；

（3）将△ABC 绕着点 O 按顺时针方向旋转 90°得到

△A3B3C3，画出△A3B3C3，并写出△A3B3C3 的各顶点的

坐标．

19.（推理能力）（15 分）已知△ABC 与△DEC 是两个大小不同的等腰直角三角形．

（1）如图 1 所示，连接 AE，DB，试判断线段 AE 和 DB 的数量和位置关系，并说明

理由；

（2）如图 2 所示，连接 DB，将线段 DB 绕 D 点顺时针旋转 90°到 DF，连接 AF，试

判断线段 DE 和 AF 的数量和位置关系，并说明理由．

A C D

B

E E

B

C A D

F

图 1 图 2

（第 19 题图）

143 144

A O

B C

y

x

（第 13 题图）

B A

C A′ B′

C′

O x

y

（第 14 题图）

D C

A B

E

F

（第 15 题图）

A

D

B C

E

（第 16 题图）

A

B

C

O

y

x

（第 18 题图）

密

封

线

学

校 ______________________班

级 ______________________姓

名 ______________________考

号 ______________________

◆

全

优

课

堂·数

学·九

年

级

上

册

145 146

一、选择题（每小题 4 分，共 48 分）

1. 下列图形中，既是轴对称图形又是中心对称图形的是 （ ）

A B C D

2. 已知点 A（a，2）与点 B（5，b）关于原点对称，则 a，b 值分别是 （ ）

A． a=2，b=5 B． a=5，b=2 C． a=-5，b=2 D． a=-5，b=-2

3. 若关于 x 的方程 2x2

-3m-x+m2

=0 的一个根是 0，则 m 的值为 （ ）

A． 0 B． 3 C． 0 或 3 D． 0 或-3

4. 直线 y=kx 经过第二、四象限，则抛物线 y=kx2

+2x+k2 图象的大致位置是 （ ）

O

y

x O

y

x O

y

x O

y

x

A B C D

5.（易错点）一元二次方程 mx2

+mx- 1

2 =0 有两个相等的实数根，则 m 的值为 （ ）

A． 0 B． 0 或-2 C． -2 D． 2

6. 如图，△ABC 中，∠CAB=70°，在同一平面内，将△ABC

绕点 A 旋转到△AB′C′的位置，使得 C′C∥AB，则∠CAB′

等于 （ ）

A． 30° B． 25°

C． 15° D． 10°

7. 二次函数 y=x2

+bx+c 的图象是由 y=x2

+4x-1 的图象向右平移 1 个单位长度，再

向下平移2 个单位长度得到的，则 b= （ ）

A． 1 B． 2 C． 3 D． 4

8. 已知二次函数的图象（0≤x≤4）如图所示，关于该函数在所给自变量的取值范

围内，下列说法正确的是 （ ）

A． 有最大值 2，有最小值-2.5 B． 有最大值 2，有最小值 1.5

C． 有最大值 1.5，有最小值-2.5 D． 有最大值 2，无最小值

1 2 3 4

2

1.5

1

-1

-2 -2.5

O

y

x

B

A O

y

x

3

1

O 4

C

t/s

h/m

（第 8 题图） （第 10 题图） （第 11 题图）

9.一幅长 60 cm，宽 40 cm 的矩形树叶画四周镶一条金色的纸边，制成一幅矩形

挂图，若要使整个挂图的面积是 3 100 cm2

，设金色纸边的宽为 x cm，则满足的

方程是 （ ）

A．（60+x）（40+x）=3 100 B．（60+2x）（40+2x）=3 100

C．（60+2x）（40+x）=3 100 D．（60+x）（40+2x）=3 100

10. 如图，点 O 为平面直角坐标系的原点，点 A 在 x 轴上，△OAB 是边长为 4 的等

边三角形，以 O 为旋转中心，将△OAB 按顺时针方向旋转 60°，得到△OA′B′，那

么点 A′的坐标为 （ ）

A．（2，2姨3 ） B．（-2，4） C．（-2，2姨2 ） D．（-2，2姨3 ）

11. 如图，铅球的出手点 C 距地面 1 m，出手后的运动路线是抛物线，出手后 4 s 达

到最大高度 3 m，则铅球运行路线的解析式为 （ ）

A． h=- 3

16 t

2 B． h=- 3

16 t

2

+t C． h=- 1

8 t

2

+t+1 D． h=- 1

3 t

2

+2t+1

12.（重点）已知二次函数 y=ax2

+bx+c（a≠0）的图象如图所示，则下

列结论：①2a+b=0；②当 x＜1 时，y 随 x 的增大而增大；③c＜0；

④9a+3b+c=0；⑤b2

-4ac＞0，其中正确的有 （ ）

A． 2 个 B． 3 个

C． 4 个 D． 5 个

二、填空题（每小题 4 分，共 12 分）

13. 用配方法解一元二次方程 x2

-2x-4=0 时，可变形为（x-1）2

=a 的形式，则 a 的值

为 ________.

题 号 一 总 分

分 值

二 三

期中高频考题组合卷

（时间：90 分钟 满分：１2０ 分）

A B

C C′

B′

（第 6 题图）

y

-1

O x=1

x

（第 12 题图）

147 148

14. 如图所示的图案，可以看作是由大写字母 A 绕中心连续旋转，

每次旋转 _____ 度构成的.

15. 已知二次函数 y=ax2

-4ax+3a.

（1）若 a=1，则函数 y 的最小值为 _______；

（2）若当 1≤x≤4 时，y 的最大值是 4，则 a 的值为 _____.

三、解答题（共 60 分）

16.（运算能力）（10 分）解方程：

（1）4x2

-3x-1=0； （2）（2x+1）2

=3（2x+1）.

17.（12 分）已知一元二次方程（k-2）x2

-4x+2=0 有两个不相等的实数根．

（1）求 k 的取值范围；

（2）如果 k 是符合条件的最大整数，且一元二次方程 x2

-4x+k=0 与 x2

+mx-1=0 有

一个相同的根，求此时 m 的值．

18.（12 分）把两个三角形按如图 1 放置，其中∠ACB=∠DEC=90°，∠CAB=45°，

∠CDE=30°，且 AB=6，DC=7，把△DCE 绕点 C 顺时针旋转 15°得到△D1CE1，如图

2，这时 AB 与 CD1 相交于点 O，与 D1E1 相交于点 F．

（1）求∠ACD1 的度数；

（2）求线段 AD1 的长．

19.（模型观念）（12 分）某果园有果树 80 棵，现准备多种一些果树提高果园产量，但是

如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之

降低．若该果园每棵果树产果 y（kg）与增种果树 x（棵）之间的函数关系如图所示．

（1）求 y 与 x 之间的函数解析式；

（2）在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实 6 750 kg？

（3）当增种果树多少棵时，果园的总产量 w（kg）最大？ 最大产量是多少千克？

74

66

12 28

y（kg）

O x（棵）

（第 19 题图）

20.（难点）（14 分）若两条抛物线的顶点相同，则称它们为“友好抛物线”，抛物线 C1：

y1=-2x2

+4x+2 与 C2：y2=-x2

+mx+n 为“友好抛物线”．

（1）求抛物线 C2 的解析式；

（2）点 A 是抛物线 C2 上在第一象限的动点，过 A 作 AQ⊥x 轴，Q 为垂足，求 AQ+

OQ 的最大值；

（3）设抛物线 C2 的顶点为 C，点 B 的坐标为（-1，4），问在 C2 的对称轴上是否存

在点 M，使线段 MB 绕点 M 逆时针旋转 90°得到线段 MB′，且点 B′恰好落在抛物

线 C2 上？ 若存在，求出点 M 的坐标，若不存在，请说明理由．

O

C

y

x

（第 20 题图）

（第 14 题图）

A

D

C E B

A D1

E1

O

F

C B

图 1 图 2

（第 18 题图）