闫老师专用教案

1

七上第 1 周秋季讲义知识点 1 棱柱的相关概念

1.棱和侧棱的定义：在棱柱中任何相邻两个面的交线，都叫做 棱 ；相邻两个侧面的交线叫做侧棱.2.棱柱所有的侧棱长都___相等_____.棱柱的上、下底面的形状 相同 ，侧面的形状都是平行四边形.3.长方体，正方体都是___四棱柱___.

4.棱柱可以分为 直棱柱和斜棱柱 .例题

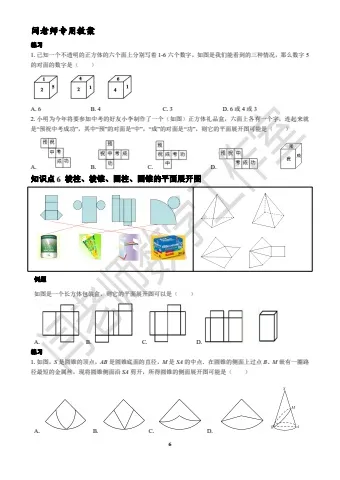
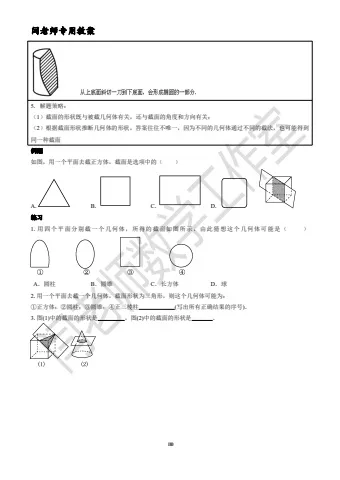
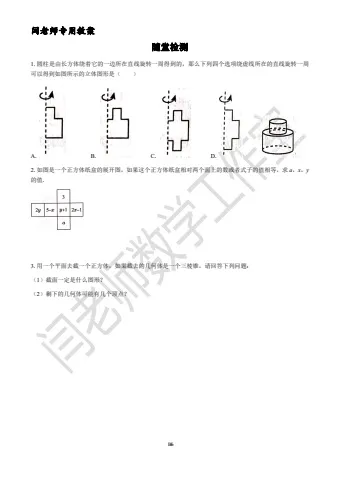
1.下列所示的几何体中，棱柱有（ ）

A.2 个 B.3 个 C.4 个 D.5 个练习

1.有下列关于棱柱的说法正确的是： （ ）

①棱柱的所有面都是平面； ②棱柱的所有棱长都相等；③棱柱的所有侧面都是长方形和正方形；④棱柱的侧面个数与底面边数相等；⑤棱柱的上、下底面形状相同，大小相等A.2 个 B.3 个 C.4 个 D.5 个知识点 2 棱柱的特征

棱柱 面的个数 顶点个数 棱的条数n 棱柱

n+2

（侧面数+上、下底面数）

2n

（上、下底面顶点数）

3n

（侧棱数+上、下底面棱数）例题

1.经过五棱柱的一个顶点的棱有（ ）

A. 3 条 B.4 条 C.5 条 D.6 条练习

1.一个棱柱有 12 个顶点，所有侧棱长的和是 48 厘米，则每条侧棱长是 厘米.

2.如果一个直棱柱有 30 条棱，那么该棱柱有 个面.

3.一个直棱柱有12条棱，则它是 棱柱．

闫老师专用教案

2

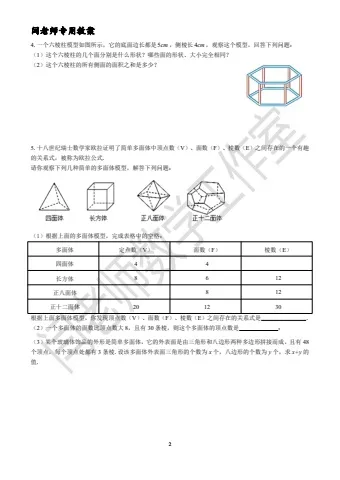
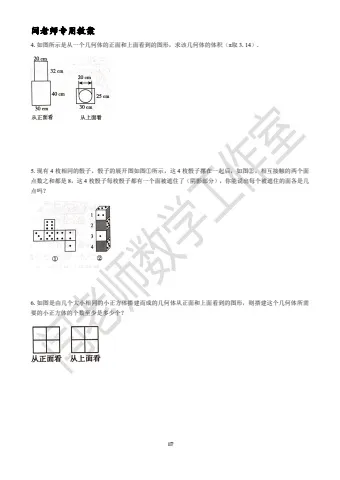
4.一个六棱柱模型如图所示，它的底面边长都是5cm ，侧棱长 4cm，观察这个模型，回答下列问题：（1）这个六棱柱的几个面分别是什么形状？哪些面的形状、大小完全相同？（2）这个六棱柱的所有侧面的面积之和是多少？

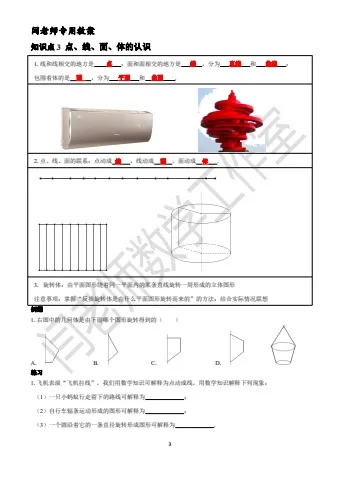
5.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，被称为欧拉公式.请你观察下列几种简单的多面体模型，解答下列问题：

（1）根据上面的多面体模型，完成表格中的空格：

多面体 定点数（V） 面数（F） 棱数（E）四面体 4 4

长方体 8 6 12

正八面体 8 12

正十二面体 20 12 30

根据上面多面体模型，你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是．（2）一个多面体的面数比顶点数大 8，且有 30 条棱，则这个多面体的顶点数是；（3）某个玻璃体饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有48个顶点，每个顶点处都有 3 条棱.设该多面体外表面三角形的个数为 x 个，八边形的个数为y 个，求x+y的值.

闫老师专用教案

3

知识点 3 点、线、面、体的认识

1.线和线相交的地方是 点 ；面和面相交的地方是 线 ，分为 直线和曲线；包围着体的是 面 ，分为 平面 和 曲面 .

2.点、线、面的联系：点动成 线 ，线动成 面 ，面动成 体 .

3. 旋转体：由平面图形绕着同一平面内的某条直线旋转一周形成的立体图形注意事项：掌握“反推旋转体是由什么平面图形旋转而来的”的方法：结合实际情况联想例题

1.右图中的几何体是由下面哪个图形旋转得到的（ ）

A. B. C. D.练习

1.飞机表演“飞机拉线”，我们用数学知识可解释为点动成线，用数学知识解释下列现象：（1）一只小蚂蚁行走留下的路线可解释为 ；

（2）自行车辐条运动形成的图形可解释为 ；

（3）一个圆沿着它的一条直径旋转形成图形可解释为 .

闫老师专用教案

4

2.围成几何体的若干个面中，至少有一个是曲面的几何体有（ ）

①三棱锥 ②圆柱 ③圆锥 ④球 ⑤长方体 ⑥六棱柱

A. 1 个 B. 2 个 C.3 个 D.4 个3.观察下图，请把右边的图形绕着给定的直线旋转一周后可能形成的几何体选出来（）A. B. C. D.知识点 4 正方体的平面展开图

1.展开的定义：将一个立体图形适当剪开，平铺在一个平面内，得到一个平面图形，这个平面图形就叫做立体图形的 展开图 .

2.一个立体图形按不同方式展开，可能得到不同的展开图.

3.正方体的平面展开图

记忆口诀：（1−4−1）（2−3−1）（2−2−2）（3−3）总面六个不能少，凹字、田字不能有例题

图 1 和图 2 中所有的正方形都全等，将图 1 的正方形放在图 2 中的①②③④某一位置，所组成的图形不能围成正方体的位置是（ ）

A．① B．② C．③ D．④

闫老师专用教案

5

练习

1.下面图形中，不能折成无盖的正方体盒子的是（ ）

A. B. C. D.

2.如图是一个正方体纸盒的外表面展开图，则这个正方体是（ ）

A． B． C． D．

3.如图所示的正方体的展开图是（ ）

A. B. C. D.

4.如图的正方体盒子的外表面上画有 3 条粗黑线，将这个正方体盒子的表面展开（外表面朝上），展开图可能是（ ）

A. B. C. D.知识点 5 正方体平面展开图的相对面

在正方体平面展开图中找相对面的方法：同行同列隔个面，“Z 字找两端”例题

左图是一个正方体的表面展开图，已知正方体的每一个面都有一个实数，且相对面上的两个数互为倒数，则 x 的值为 .

闫老师专用教案

6

练习

1.已知一个不透明的正方体的六个面上分别写着 1-6 六个数字，如图是我们能看到的三种情况，那么数字5的对面的数字是（ ）

A.6 B.4 C.3 D.6 或4 或3

2.小明为今年将要参加中考的好友小李制作了一个（如图）正方体礼品盒，六面上各有一个字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是（）A. B. C. D.知识点 6 棱柱、棱锥、圆柱、圆锥的平面展开图例题

如图是一个长方体包装盒，则它的平面展开图可以是（ ）

A. B. C. D.练习

1.如图，S 是圆锥的顶点，AB 是圆锥底面的直径，M 是 SA 的中点．在圆锥的侧面上过点B、M嵌有一圈路径最短的金属丝，现将圆锥侧面沿 SA 剪开，所得圆锥的侧面展开图可能是（）A. B. C. D.

闫老师专用教案

7

2.设计制作一个圆柱形的包装纸盒，下列表面展开图的草图正确的是（ ）A． B． C． D．

3.如图所示，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色，该几何体的表面展开图是（ ）

A. B. C. D.知识点 7 能折成棱柱的平面图形的特征

1．并不是所有立体图形都能展开为平面图形，如球体.

2．并不是所有平面图形都能折成几何体，要符合一定的条件.

3．若能折成棱柱，需符合以下 3 个特点：

① 底面边数=侧面面数. ② 两个底面完全一样，且在侧面展开图的两端. ③ 四棱柱的平面展开图中只有 5 条相连的棱.例题

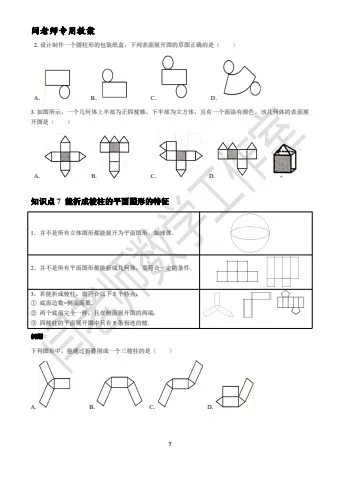
下列图形中，能通过折叠围成一个三棱柱的是（ ）

A. B. C. D.

闫老师专用教案

8

练习

1.下列图形经过折叠不能围成棱柱的是（ ）

A. B. C. D.

2.下列四个图形能围成棱柱的有几个（ ）

A．0 个 B．1 个 C．2 个 D．3 个知识点 8 用平面截一个几何体

1.截面：用一个平面去截一个几何体，截出的面叫做截面.

2.理论依据：面面相交得交线，交线相连得截面.

3.可能形状：三角形、四边形、五边形、六边形、圆、椭圆，类似拱形的形状等.三角形 四边形 五边形 六边形 圆 椭圆类似拱形的形状4. 常见几何体的截面：

（1）正方体的截面

闫老师专用教案

9

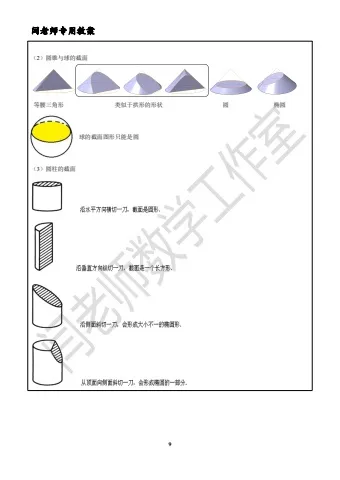
（2）圆锥与球的截面

等腰三角形 类似于拱形的形状 圆椭圆球的截面图形只能是圆

（3）圆柱的截面

闫老师专用教案

1100

5. 解题策略：

（1）截面的形状既与被截几何体有关，还与截面的角度和方向有关；

（2）根据截面形状推断几何体的形状，答案往往不唯一，因为不同的几何体通过不同的截法，也可能得到同一种截面

例题

如图，用一个平面去截正方体，截面是选项中的（ ）

A. B. C. D.练习

1.用四个平面分别截一个几何体，所得的截面如图所示，由此猜想这个几何体可能是（）A．圆柱 B．圆锥 C．长方体 D．球2.用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：①正方体；②圆柱；③圆锥；④正三棱柱 (写出所有正确结果的序号)．3.图(1)中的截面的形状是 ，图(2)中的截面的形状是 ．

闫老师专用教案

1111

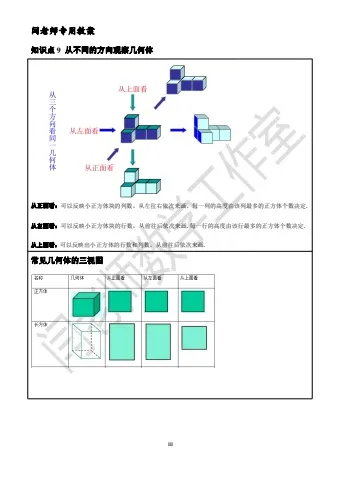
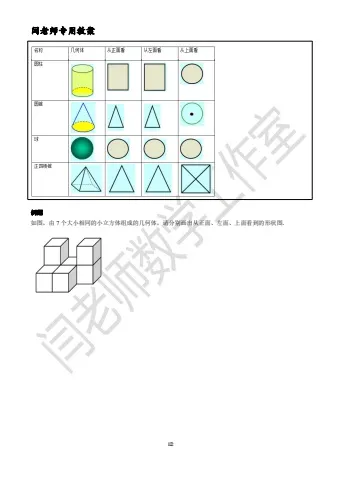
知识点 9 从不同的方向观察几何体

从正面看：可以反映小正方体块的列数，从左往右依次来画，每一列的高度由该列最多的正方体个数决定.从左面看：可以反映小正方体块的行数，从前往后依次来画.每一行的高度由该行最多的正方体个数决定.从上面看：可以反映出小正方体的行数和列数，从前往后依次来画.常见几何体的三视图

闫老师专用教案

1122

例题

如图，由 7 个大小相同的小立方体组成的几何体，请分别画出从正面、左面、上面看到的形状图.

闫老师专用教案

1133

练习

下图是由七块积木搭成的，这七块积木都是大小相同的正方体，棱长为 1，请画出这个几何体从正面、左面、上面看到的形状图，求出该几何体的表面积.知识点 10 根据俯视图画主视图和左视图

例题

如图所示，这是两个由小立方体搭成的几何体的俯视图，小正方形中的数字表示该位置的小立方体的个数，请画出相应几何体从正面看和左面看所得到的图形.

练习

下图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请画出相应几何体从正面看和左面看所得到的图形.

闫老师专用教案

1144

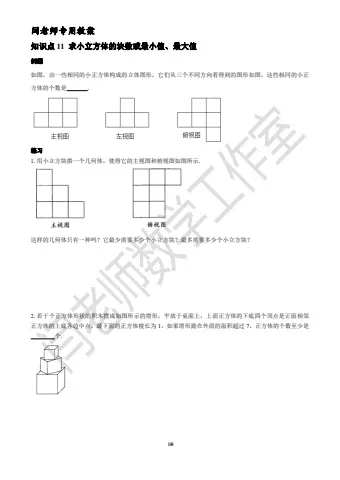
知识点 11 求小立方体的块数或最小值、最大值例题

如图，由一些相同的小正方体构成的立体图形，它们从三个不同方向看得到的图形如图，这些相同的小正方体的个数是 .练习

1.用小立方块搭一个几何体，使得它的主视图和俯视图如图所示.这样的几何体只有一种吗？它最少需要多少个小立方块？最多需要多少个小立方块？2.若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是正面相邻正方体的上底各边中点，最下面的正方体棱长为 1，如果塔形露在外面的面积超过7，正方体的个数至少是个.

闫老师专用教案

1155

知识点 12 求几何体表面积

例题

图（1）（2）（3）（4）都是由棱长为 1 的正方体叠成的图形.如第（1）个图形的表面积为 6 个平方单位，第（2）个图形的表面积为 18 个平方单位，第（3）个图形的表面积是 36 个平方单位.依此规律，则第（5）个图形的表面积是 个平方单位.练习

1.一个画家有 14 个边长为 1 的正方体，他在地面上把它们摆成如图的形式，然后他把露出的表面都涂上颜色，那么被涂颜色的总面积为（ ）

A.19 B.41 C.33 D.34

2.如图是某几何体的三视图

（1）指出这个几何体的名称；

（2）画出它的表面展开图；

（3）若主视图的宽为 4cm ，长为5cm ，左视图的宽为3cm .俯视图为直角三角形，且斜边长为5cm.求这个几何体中所有的棱长和为多少？它的表面积为多少？它的体积为多大？

闫老师专用教案

1166

随堂检测1.圆柱是由长方体绕着它的一边所在直线旋转一周得到的，那么下列四个选项绕虚线所在的直线旋转一周可以得到如图所示的立体图形是（ ）

A. B. C. D.

2.如图是一个正方体纸盒的展开图，如果这个正方体纸盒相对两个面上的数或者式子的值相等，求a，x，y的值.

3.用一个平面去截一个正方体，如果截去的几何体是一个三棱锥，请回答下列问题：（1）截面一定是什么图形？

（2）剩下的几何体可能有几个顶点？

闫老师专用教案

1177

4.如图所示是从一个几何体的正面和上面看到的图形，求该几何体的体积（π取3.14）.

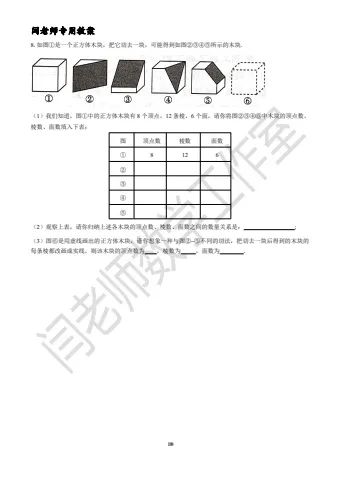
5.现有 4 枚相同的骰子，骰子的展开图如图①所示，这 4 枚骰子摞在一起后，如图②，相互接触的两个面点数之和都是 8，这 4 枚骰子每枚骰子都有一个面被遮住了（阴影部分），你能说出每个被遮住的面各是几点吗？

6.如图是由几个大小相同的小正方体搭建而成的几何体从正面和上面看到的图形，则搭建这个几何体所需要的小正方体的个数至少是多少个？

闫老师专用教案

1188

7.从正面和上面看由一些大小相同的小正方体组成的简单几何体得到的形状如图所示. （1）请你画出这个几何体的一种从正面看到的形状图；

（2）若组成这个几何体的小正方体的个数为 n，请你写出 n 的所有可能值.

闫老师专用教案

1199

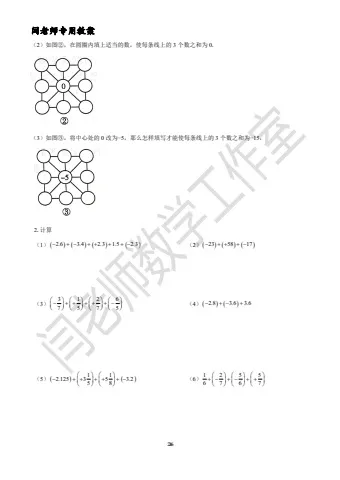
8.如图①是一个正方体木块，把它切去一块，可能得到如图②③④⑤所示的木块. （1）我们知道，图①中的正方体木块有 8 个顶点，12 条棱，6 个面，请你将图②③④⑤中木块的顶点数、棱数、面数填入下表；

图 顶点数 棱数 面数

① 8 12 6

②

③

④

⑤

（2）观察上表，请你归纳上述各木块的顶点数、棱数、面数之间的数量关系是：;

（3）图⑥是用虚线画出的正方体木块，请你想象一种与图②~⑤不同的切法，把切去一块后得到的木块的每条棱都改画成实线，则该木块的顶点数为 ，棱数为 ，面数为 .

闫老师专用教案

2200

七上第 2 周秋季讲义知识点 1 正数和负数的概念与意义

正数：为了表示具有相反意义的数，把其中的一个量

规定为正的，用正数来表示.举例：0.2， 7

1 ，8，π，...负数：把与正的量意义相反的量规定为负的，用负数来表示.举例：−1，−0.56，− 7

1 ，−0.10101...，...格外注意：

1. 对于正数和负数而言，不能简单地理解为带“+”的数是正数，带“−”的数是负数.

2. 负数是在正数的前面加上“+”，如−5，−（+7）等都是负数，负数中的“−”不能省略，如−5 省略“−”就是5，变成正数了.

3. 0 既不是正数，也不是负数.例题

下列各数：0，

12 ， (1) ，

1

2  ， 2 (1) ， 3 (3) ，其中是负数的有（ ）A．1个 B． 2 个 C．3个 D． 4 个练习

1.−a 一定是（ ）

A.正数 B.负数 C.0 D.以上选项都不正确2.将下列具有相反意义的量用线连接起来：

向东走 100 m 输球 4 个

胜球 4 个 亏损 2 万元

盈利 2000 元 运进化肥 200 t

高于海平面 200 m 向西走 15 m

运出化肥 100 t 低于海平面 300 m

3.下列语句：

①不带“−”号的数都是正数；②一个正数的前面加上负号就是负数；③数 7 没有符号；④不是正数的数一定是负数，不是负数的数一定是正数.其中错误的有 （填序号）.

闫老师专用教案

2211

知识点 2 有理数的分类

··· 0

··· 1 1 1

··· 2 3 4

1 1 1

··· 2 3 4

 

 



















 

正整数，如1,2,3,整数

负整数，如-1,-2,-3,有理数

正分数，如 ，， ,分数

负分数，如- ，- ，- ,

··· 111··· 2340

···111···234 

 



















 

正整数，如1,2,3,正有理数正分数，如，，,有理数负整数，如-1,-2,-3,负有理数负分数，如-，-，-,温馨提示：

分数可以转化为有限小数或者无限循环小数，反过来也成立！

例题

把下列各数填在相应的大括号中:

2 2014

2

,( 1) , 0.25, | 3 |,1.5, 1

3

2  (4),0,     

整数集合{ }

分数集合{ }

负数集合{ }

练习

1.下列选项中，大括号中所填的数正确的是（ ）

A.正数集合：

1

2 1 5

2

, ,  

 

  ，， B.非负数集合：0，-1，-2.5,C.分数集合：

1

2 5 5

3

.  

 

  - ，，， D.整数集合：

1

3 5

2

,  

 

  ，-

2.下列说法错误的是（ ）

A. 2

π 不是有理数 B.0.8 是有理数 C.自然数就是非负整数 D.自然数就是正整数3.对于

4 5 2

1 8 6 7 0 4 101 0 05 9

5 6 3  , , . , , , , , , . , 这些数，下列说法中，正确的是（）A.只有 1，−7，+101，−9 是整数 B.其中有三个数是正整数

C.非负数有

5

1 8 6 0 101

6

, . , , , D.只有

4 2

4

5 3  , 是负分数

闫老师专用教案

2222

知识点 3 认识数轴

1. 数轴的定义：规定了原点、正放向、单位长度的直线叫做数轴.温馨提示：① 原点、正方向、单位长度称为数轴的三要素，三者缺一不可！② 正方向一般规定为向右的方向！③ 单位长度可以根据实际情况确定！2. 数轴的画法（4 步法）：

第一步，画一条水平的直线；

第二步，在这条直线上的适当位置取一点作为原点；

第三步，确定正方向，用箭头表示出来；

第四步，确定单位长度，用细短线画出，并对应标记上数字.温馨提示：所有的有理数都可以在数轴上找到它的对应点3. 数轴的应用：

① 数轴上两个点表示的有理数，右边的数总是比左边的大，所以通过数轴上数字的左右位置可以比较出两个数的大小关系；

② 根据正、负数对应的点在数轴上的位置，可以归纳有理数比较大小的规律：正数都大于0，负数都小于0，正数比所有的负数都大.例题

根据给出的数轴及已知条件，解答下面的问题：

（1）已知点 A、B、C 表示的数分别为 3

2

5

1， ， .观察数轴，与点 A 的距离为3 的点表示的数是__________，A、B 两点之间的距离为________；

（2）数轴上，点 B 关于点 A 的对称点表示的数为__________；

（3）若数轴上 P、Q 两点间的距离为 a （ P 在Q 左侧），表示数b 的点到 P、Q两点的距离相等，将数轴折叠，当 P 点与Q 点重合时，点 P 表示的数是__________，点Q 表示的数是__________（用含a，b的式子表示这两个数）.

闫老师专用教案

2233

练习

1.如图，圆的周长为 4 个单位长度，在圆的四等分点处标上字母 A、B、C、D，先将圆周上的字母A对应的点与数轴的数字 1 对应的点重合，若将圆沿着数轴向左滚动，那么数轴上的－2019 所对应的点将于圆周上字母（ ）所对应的点重合. A.A B.B C.C D.D

2.如图,A、B 两点在数轴上表示的数分别为 a、b ，下列式子成立的是（ ）A. ab  0 B. (b 1)(a 1)  0 C. a  b  0 D. (b 1)(a 1) 03.数轴上点 A 表示的数是−3，将点 A 在数轴上平移 7 个单位长度得到点 B，则点B 表示的数是（）A.4 B. −4 或 10 C.−10 D.4 或−10

知识点 4 相反数和绝对值

1. 相反数的概念：一般地，如果两个数只有符

号不同，那么我们就说其中一个数是另一个数的

相反数，也说这两个数互为相反数.特别地，0 的相反数是 0.例如：6 的相反数是−6，−3 的相反数是 3

温馨提示：

① 在数轴上，互为相反数的两个数对应的点位于原点的两侧，且到原点的距离相等. ② 数轴上表示互为相反数的两个数的点关于原点对称.③ 相反数是成对的，不能说单独的一个数是相反数，只能说一个数是另一个数的相反数2. 绝对值的概念：在数轴上，一个数所对应的

点与原点的距离叫做这个数的绝对值. ① 一个正数的绝对值是它本身，例如： 4 =4，

+1.7 =1.7

② 一个负数的绝对值是它的相反数，例如：

2  2，

5.2  5.2

③ 0 的绝对值是 0

温馨提示：

① 绝对值可以用来比较数的大小，例如比较两个负数的大小：在数轴上，由于绝对值是表示数的点到原点的距离，则离原点越远的点表示的数的绝对值越大.② 负数的绝对值越大，表示这个数的点就越靠近左边.因此，两个负数比较大小，绝对值大的反而小.

闫老师专用教案

2244

例题

已知数 a ，b ，c 的大小关系如图所示，则下列各式：

① abc  0；② a  b  c  0；③   1

c

c

b

b

a

a

；④bc  a  0 ；⑤ a  b c abc2a其中正确的是 .(写序号)

练习

1.a，b，c，d 四个数在数轴上的对应点的位置如图所示，这四个数中，绝对值最大的是（）A．a B．b C．c D．d

2.下列说法中，正确的是（ ）

A. 8 是求−8 的相反数

B. 8 表示的意义是数轴上表示−8 的点到原点的距离

C. 8 表示的意义是数轴上表示−8 的点到原点的距离是−8

D.以上都不对

3.把下列各数表示在数轴上，并用＜将原数连接起来.

2.5, 2

1 1 ,  1 , 2  2 , 

2  2

4.我们知道， a 可以理解为 a  0 ，它表示：数轴上表示数 a 的点到原点的距离，这是绝对值的几何意义，进一步地，数轴上的两个点 A、B，分别用数 a 、b 表示，那么 A、B 两点之间的距离为AB= ab，反过来，式子 a  b 的几何意义是：数轴上表示数 a 的点和表示数b 的点之间的距离，利用此结论，回答以下问题：

（1）数轴上表示数 8 的点和表示数 3 的点之间的距离是 . （2）数轴上点 A 用数 a 表示，若 a =5，那么 a 的值为 . （3）数轴上点 A 用数 a 表示，

①若 a  3 =5，那么 a 的值是 . ②当 a  2  a  3  5 时，数 a 的取值范围是 ，这样的整数 a 有 个. ③ a  3  a  2017 有最小值，最小值是 .

闫老师专用教案

2255

知识点 5 有理数的加法

法则 1：

同号两数相加：取相同的符号，并把绝对值相加

例如：2+3=5；（−2）+（−3）= −5

温馨提示：① 加法的法则指出，两个有理数相加的结果由两部分组成：先确定和的符号，再把两数的绝对值相加或者相减，得到的是和的绝对值. ② 在加法运算中，最容易出错的就是符号，所以在运算时要格外注意符号问题！法则 2：

异号两数相加：

① 绝对值相等时，和为 0（即互为相反的两个数相加等于 0）

② 绝对值不相等时，取绝对值较大的数的符号，并用较大的绝对值

减去较小的绝对值

例如：5+（−5）=0；（−3）+2= −（3−2）= −1

③ 一个数和 0 相加，结果仍然是这个数

加法运算律：

① 加法交换律： a  b  b  a ，例如：2  3  3  2

② 加法结合律：a  b  c  a  b  c  ，

例如：3  2  2  3  2  2  3  

温馨提示：在进行有理数加法运算时，运用加法交换律和加法结合律往往能使运算变得简便！例题

下列计算：① 0.7  0.7  0 ;②7  3  10 ；③5  0  5 ；④

2 26 63 3     

.其中错误的有（ ）

A．1 个 B．2 个 C．3 个 D．4 个练习

1.还记得小时候经常玩的填数游戏吗？一起用有理数来试试吧！

（1）请在图①的各个圆圈内填上适当的数，使每个圆圈内的数都等于与它相邻的两个数的和.

闫老师专用教案

2266

（2）如图②，在圆圈内填上适当的数，使每条线上的 3 个数之和为 0.

（3）如图③，将中心处的 0 改为−5，那么怎样填写才能使每条线上的 3 个数之和为−15，2.计算

（1）2.6  3.4  2.3 1.5  2.3  （2）23  58 17

（3）

3 1 2 6

7 5 7 5

       

              

        （4）2.8  3.6 3.6（5）    1 1

2 125 3 5 3 2

5 8

. .             

    （6）

1 2 5 56 7 6 7            

     

闫老师专用教案

2277

知识点 6 有理数的减法

法则：

减去一个数，等于加上这个数的相反数，

例如：3  9  3  9

温馨提示：学了有理数之后，小学里减去“不够减”的矛盾解决了.做有理数的减法时，根据减法法则，将减法化为加法来做，即将减号改为加号，将减数改为它的相反数.例题

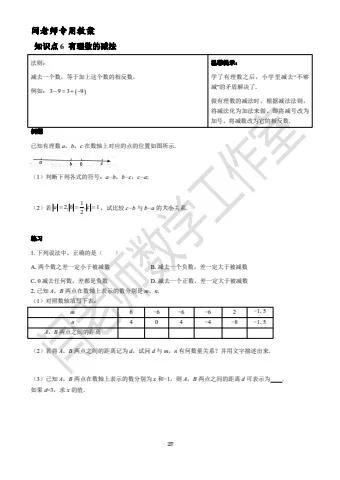
已知有理数 a，b，c 在数轴上对应的点的位置如图所示. （1）判断下列各式的符号：a−b，b−c，c−a;

（2）若

1

2 1

2

a  , b  , c  ，试比较 c−b 与 b−a 的大小关系.练习

1.下列说法中，正确的是（ ）

A.两个数之差一定小于被减数 B.减去一个负数，差一定大于被减数C.0 减去任何数，差都是负数 D.减去一个正数，差一定大于被减数2.已知 A，B 两点在数轴上表示的数分别是 m，n. （1）对照数轴填写下表：

m 6 −6 −6 −6 2 −1.5

n 4 0 4 −4 −8 −1.5

A，B 两点之间的距离

（2）若将 A，B 两点之间的距离记为 d，试问 d 与 m，n 有何数量关系？并用文字描述出来. （3）已知 A，B 两点在数轴上表示的数分别为 x 和−1，则 A，B 两点之间的距离d 可表示为.如果 d=3，求 x 的值.

闫老师专用教案

2288

3.计算

（1）12  18  7 15 （2）

2 1 313 3 44                 （3）

5 11 7

1

3 6 6

        

  （4）32  27 7287（5）6.1  4.3  2.1 5.1 （6）

22 3 3815 11 511            （7）   2 3 2

3 2 1 1 75

3 4 3

.      

            

      （8）16  12 2418

闫老师专用教案

2299

随堂检测1.下列关于“0”的叙述中，正确的有（ ）

①0 是正数与负数的分界；②0 比任何负数都大；③0 只表示没有；④0 常用来表示某种量的基准.A.1 个 B.2 个 C.3 个 D.4 个2.下列关于“0”的说法中，正确的是（ ）

①是整数，也是有理数；②不是正数，也不是负数；③不是整数，是有理数；④是整数，不是自然数.A.1 个 B.2 个 C.3 个 D.4 个4.数轴上一个数与－2 的距离是 5，那么这个数是（ ）

A. ±5 B.3 或－7 C. －7 D. 3

3.（1）把有理数−3，2022，0,37，

22

7  填入表示它所在数集的圈内（如图）；（2）请你仿照（1）重新给出两个数集，并在图中的三个区域内各填入 3 个相应的有理数.

4.计算

（1）

1

2 2 2

5

.  

  

  （2）26  52 16  72

（3）42  57  84  23 （4） 43  77  27  43

（5）16  12  24  18 （6）64 17  23  68

闫老师专用教案

3300

附加题

1.在一条不完整的数轴上从左到右有点 A 、B 、C ，其中点 A 到点 B的距离为3，点C到点B的距离为7，如图所示：设点 A ， B ，C 所对应的数的和是 m . （1）若以C 为原点，则 m 的值是 . （2）若原点O 在图中数轴上，且点C 到原点O 的距离为 4，求 m的值. （3）动点 P 从 A 点出发，以每秒 2 个单位长度的速度向终点C 移动，动点Q同时从B点出发，以每秒1个单位的速度向终点C 移动，当几秒后， P 、Q 两点间的距离为 2？（直接写出答案即可）2.点 A、B 在数轴上分别表示有理数 a、b，A、B 两点之间的距离表示为|AB|，利用数形结合思想回答下列问题：

（1）数轴上表示－3 和 1 两点之间的距离是 ；

（2）数轴上表示 x 和－2 的两点之间的距离表示为 ；

（3）若 x 表示一个有理数，且－3＜x＜1，则|x－1|+|x+3|的最小值是 ；（4）若 x 表示一个有理数，且|x－1|+|x+3|＞4，则有理数 x 的取值范围是 .

闫老师专用教案

3311

3.如图在数轴上 A 点表示数 a，B 点表示数 b，a、b 满足|a+2|+|b−4|=0．

（1）点 A 表示的数为 ；

（2）若在原点 O 处放一挡板，一小球甲从点 A 处以 1 个单位/秒的速度向左运动；同时另一小球乙从点B处以 2 个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以3 个单位/秒的速度向相反的方向运动，设运动的时间为 t（秒）；

①当 t=1 时，乙小球到原点的距离= ；

②当 t= 时，甲小球与乙小球的距离为 4.5；

③当 t= 时，甲小球与乙小球的距离为 16．

抖音：866460001

32 数学加分宝4.如图，已知数轴上点 A 表示的数为 7，点 B 表示的数为−5，点 P 从点 A 出发，沿数轴以每秒3个单位长度的速度向左匀速运动，同时，另一点 Q 从原点 O 出发，也沿数轴以每秒 1 个单位长度的速度向左匀速运动，设运动时间为 t 秒（t＞0）．

（1）线段 AB 的长度为 12，数轴上点 P 和点 Q 表示的数分别为 、 （用含t 的代数式表示）；（2）在点 P 和点 Q 的运动过程中，经过多少秒点 P 追上点 Q？经过多少秒点B 恰为PQ的中点？（3）运动过程中，若时间 t 总满足|t+7|−|5−t|=12，则 t 的范围是 ．

抖音：866460001

33 数学加分宝七上第 3 周秋季讲义知识点 1 有理数的加减混合运算

例题

阅读下列计算过程，并回答问题：

  

  

 

 

1 2

3 2 7 8

3 3

1 2

3 2 7 8

3 3

1 2

3 2 7 8

3 3

1 11

10

. .

. .

. .    

           

  

       

    

第一步

第二步

第三步

第四步

（1）写出计算过程中所用到的运算律，并指出是哪一步；

（2）写出第二步的加法运算法则.练习

1.下列各题中，运用结合律变形错误的是（ ）

A,1 0.25  0.75 1 0.25  0.75 

 

B.1 2  3  4  5  6  1 2  3  4  5  6 

C. 3 1 1 2 3 1 1 2

4 6 2 3 4 6 2 3

              

   

D. 7  3  8  6  2  7  3  8  6  2 

 

2.已知 a  4,b  5,c  7 ，求 a  b  c 的值.

抖音：866460001

34 数学加分宝3.阅读下面的解题过程并填空：

计算：53.27  18  21  46.73 15  21

解：

 

       =53 27+18 21+46.73 15+21 = 53 27+46 73 21 21 18 15 =100+0+3 =103

.

. . 

    原式 第一步

第二步计算过程中，第一步是把原式化成 的形式；

第二步是根据 得到的，目的是 .请你根据以上的解题技巧进行计算：

2 1 2 1

21 3

3 4 3 4

               

     

4.计算

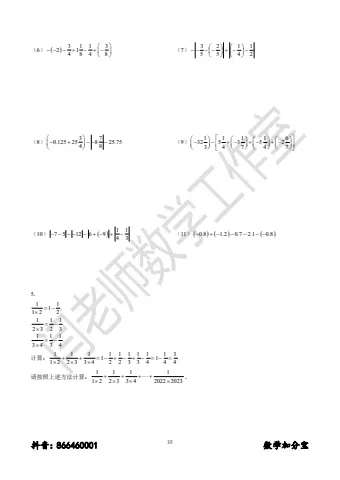
（1）

3 1 2 3 1 1

2 3 3 2 1 1

5 4 5 4 2 3

     

             

      （2）     10 75 3 0 2508758 .    . . （3）

5 5 1 3

4 3 2 1

6 8 6 8

       

  （4）

1 1 1

3 2 5

3 2 6

      

 

（5）10082  10068  10094   10086  10079  10082 

抖音：866460001

35 数学加分宝（6）   3 1 1 3

2 1

4 8 4 8

         

  （7）

3 2 1 15 5 4 2               

（8）

3 7

0 125 25 8 25 75

4 8

. .  

 

       （9）

1 1 1 1632 5 3 523 4 7 47                      （10）   1 1

7 5 12 6 9

4 3          （11）0.8  1.2  0.7 2.10.85.1 1

1

1 2 2

1 1 1

2 3 2 3

1 1 1

3 4 3 4

,

,

.  



 



 



计算：

1 1 1 1 1 1 1 1 1 3

1 1

1 2 2 3 3 4 2 2 3 3 4 4 4

          

  

请按照上述方法计算：

1 1 1 1

1 2 2 3 3 4 2022 2023

    

   

.

抖音：866460001

36 数学加分宝知识点 2 有理数的加减混合运算的应用

例题

1.足球训练中，为了训练球员快速抢断转身，教练在东西方向的足球场上画了一条直线，要求球员在这条直线上进行折返跑训练，如果约定向西为正，向东为负，将某球员的一组折返跑练习记录如下（单位：米）： 40， 30， 50， 25， 25， 30，15， 28，16，18. （1）球员最后到达的地方在出发点的哪个方向？距出发点多远？

（2）球员训练过程中，最远处离出发点_________米. （3）球员在这一组练习过程中，共跑了多少米？

2.如图，A，B 为数轴上的两点，点 A 对应数－20，点 B 对应数 100. （1）请写出 AB 中点 M 对应的数；

（2）现有一只电子蚂蚁 P 从 B 点出发，以 6 单位长度/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A 点出发，以 4 单位长度/秒的速度向右运动，设两只电子蚂蚁在数轴上的 C 点相遇，你知道C点对应的数是多少吗？

（3）若当电子蚂蚁 P 从 B 点出发时，以 6 单位/秒的速度向左运动，同时另一只电子蚂蚁Q恰好从A点出发，以 4 单位/秒的速度也向左运动，设两只电子蚂蚁在数轴上的 D 点相遇，你知道D 点对应的数是多少吗？

抖音：866460001

37 数学加分宝练习

1.将一根 12 cm 长的木棒和一根 9 cm 长的木棒捆在一起，长度为 17 cm，则两根木棒的捆绑长度（重叠部分的长度）为 cm.

2.某景区一电瓶小客车接到任务从景区大门出发，向东走 2 千米到达 A 景区，继续向东走2.5 千米到达B景区，然后又回头向西走 8.5 千米到达 C 景区，最后回到景区大门．

（1）以景区大门为原点，向东为正方向，以 1 个单位长表示 1 千米，建立如图所示的数轴，请在数轴上表示出上述 A、B、C 三个景区的位置．

（2）若电瓶车充足一次电能行走 15 千米，则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务？请计算说明．

3.下表是在汛期中防汛指挥部对河流做的一星期的水位测量（单位：cm）.（注：此河流的警戒水位为55厘米，“  ”表示比河流的警戒水位高，“－”表示比河流的警戒水位低）

星期 一 二 三 四 五 六日水位记录  2.4  0.6  4.0 1.6  3.5  2.0 1.5（1）本周河流水位最高的一天是_______，最低的一天是________，这两天的实际水位分别是________，________. （2）完成下面的本周水位变化表.（上周末河流的水位比警戒水位低 0.7 厘米，注：规定水位比前一天上升用“  ”，比前一天下降用“－”，不升不降记为 0）

星期 一 二 三 四 五 六 日水位变化

求：与上周末相比，本周末河流水位上升了还是下降了？变化了多少？（要．求．写．出．求．解．过．程．）

抖音：866460001

38 数学加分宝4.下表列出了国外几个城市与北京的时差，现在的北京时间是上午 8:00. （1）现在的纽约时间是多少？

（2）彬彬现在想给远在巴黎的姑妈打电话，你认为合适吗？

城市 时差/时

纽约 −13

巴黎 −7

东京 +1

芝加哥 −14

随堂检测1.计算

1 1 2 3

2 4 5 10

     

           

      时，下列所运用的运算律恰当的是（ ）A. 1 1 2 3

2 4 5 10

      

            

      

B. 1 2 1 3

4 5 2 10

      

         

      

C. 1 1 2 3

2 4 5 10

      

            

      

D.以上都不对

2. 规定图形 表示运算 a−b+c，图形 表示运算 x+z−y−w.则+ =（直接写出答案）

3.我国的《洛书》中记载着世界上最古老的一个幻方：将 1~9 这 9 个数字填入3×3 的方格内，使三行、三列、两对角线上的三个数之和都相等.如图所示的幻方中，字母 m 所表示的数是.

抖音：866460001

39 数学加分宝4.数轴上点 A 表示 8，点 B 表示－8，点 C 在点 A 与点 B 之间，A 点以每秒0.5 个单位的速度先向左运动，B 点以每秒 1.5 个单位的速度向右运动，点 C 以每秒 3 个单位的速度先向右运动碰到点A后立即返回向左运动，碰到点 B 后又立即返回向右运动，运动碰到点 A 后再立即返回向左运动……三个点同时开始运动，经过 秒三个点聚于一点，这一点表示的数是 ，点 C 在整个运动的过程中，移动了个单位..

5.计算

（1）

12.3  7.2  2.3  15.2  （2）

3 7 1 2

8 5 4 3

4 9 6 9     （3）  1 1

0 5 3 6 75 5

4 2

. .        

  （4） 4.7  8.9  7.5  6 

（5）

2 1 1 1

3 6 4 2

     

           

      （6）

1 10 5 3 2 75 74 2. .          

   

6.邮递员骑车从邮局出发，先向南骑行 2 km ，到达 A 村，继续向南骑行 3 km到达B 村，然后向北骑行9km到达 C 村，最后回到邮局. （1）以邮局为原点，以向北为正方向，用 0.5 cm 表示 1 km，画出数轴，并在该数轴上表示出A、B、C三个村庄的位置. （2）C 村离 A 村有多远？

（3）邮递员一共骑了多少千米？

抖音：866460001

40 数学加分宝附加题：

1.阅读下面材料：点 A、B 在数轴上分别表示实数 a, b ，A、B 两点之间的距离表示为| AB| . （1）当 A、B 两点中有一点在原点时，不妨设点 A 在原点.如图①，| AB || OB || b || a  b |；

（2）当 A、B 两点都不在原点时，

①如图②，点 A、B 在原点右边| AB || OB |  | OA|| b |  | a | b  a | a b |；②如图③，点 A、B 在左边| AB || OB |  | OA|| b |  | a | b  (a) | a b |；③如图④，点 A、B 在原点两边，| AB || OB |  | OA|| b |  | a || a  b |；综上所述，数轴上 A、B 两点之间的距离| AB || a  b | . （3）请用上面的知识解答下面的问题：

①数轴上表示 1 和 5 的两点之间的距离是 ，数轴上表示－2 和－4 的两点之间的距离是，数轴上表示 1 和－3 的两点之间的距离是 . ②数轴上表示 x 和－1 的两点 A 和 B 之间的距离是 ，如果| AB|2 ，那么x为.③ 当| x 1|  | x  2 |取最小值时，相应的 x 的取值范围是 . ④当| x 1|  | x  2 |  | x  3 |取最小值时，相应的 x 的值是 . ⑤当| x 1|  | x  2 | 取最大值时，相应的 x 的取值范围是 .

抖音：866460001

41 数学加分宝2.埃及是世界四大文明古国之一，埃及人在 2000 多年前就发现了分数，他们把分数化成分子为1的分数来计算.后来，人们把分子为 1 的分数叫埃及分数或者单位分数.已知

1 1 1

3 4 12   ，得到

1 1 1

3 4 12   ；

已知

1 1 1

4 5 20   ，得到

1 1 1

4 5 20   ；

已知

1 1 1

5 6 30   ，得到

1 1 1

5 6 30   . （1）按照上面的规律填空：        

1 1 1 1 1 1

6 20   ,   ；

（2）已知 a，b，c 都是质数（a<b<c），且

1 1 1 1

1

a b c 30

   ，求 a+b+c 的值.

42

3.已知：b 是最小的正整数，且 a, b, c 满足 ( 5) | | 0

2

c   a  b  ，回答问题：（1）请直接写出 a, b, c 的值． a = ___, b = __, c = __ . （2）a, b, c 所对应的点分别为 A、B、C，点 P 为动点，对应的数为 x ，点 P 在 0 到2 之间运动时（即0x2时），请化简式子：| x 1|  | x 1| 2 | x  5 | （写出化简过程）

（3）在（1）（2）的条件下，点 A、B、C 开始在数轴上运动，若点 A 以每秒1 个单位长度的速度向左运动，同时，点 B 和点 C 分别以每秒 2 个单位长度和 5 个单位长度的速度向右运动，假设t 秒钟过后，若点B与点 C 之间的距离表示为 BC，点 A 与点 B 之间的距离表示为 AB．请问：BC－AB 的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．

43

七上第 4 周秋季讲义知识点 1 有理数的乘法

有理数乘法法则：

1.两数相乘，同号得正，异号得负，并把绝对值相乘；

2.任何数与 0 相乘，积仍为 0

(−4)×5= −(4×5)= −20；(−5)×(−7)= +(5×7)= 35

乘法运算律

乘法交换律：ab=ba

乘法结合律：(ab)c=a(bc)

乘法分配律：a(b+c)=ab+ac

 

   

5 3

246 8

5 324246 820 9

11

     

 

     

    例题

1.下列算式中，积为正数的是（ ）

A.−2×5 B.−6×（−2） C.0×（−1） D.5×（−3）2.数 a，b 在数轴上对应点的位置如图所示，下列判断正确的是（ ）

A. a 1 B. ab  0 C. a  b  0 D.1 a 13.下列说法中，错误的是（ ）

A.一个数同 1 相乘，仍得这个数 B.一个数同−1 相乘，得原数的相反数C.互为相反数的两数的积为 1 D.一个数同 0 相乘，得 0

4.计算

1 1 2

1 3

2 4 3

   

    

    的结果为（ ）

A. 1

4

B. 11

12

C. 11

4

D. 13

4

5.计算：−2×(−5)×(−27)= ( × × )= −270

6.计算：

（1）    6

12 5 4

7

.       

  （2）

1 1 1

24

6 2 3

 

   

  （3）

1 41

4 5   

   

   

（4）     1

4 96 0 25

48

    .  （5）8 0.017 125 （6）7324187.  

  

44

练习

1.下列各组数互为倒数的是（ ）

A. 1

0 25

4

与 . B. 1

4

4

与 C. 0.1与10 D. 1

a

a

与2.下列说法中，正确的是（ ）

①两个正数中倒数大的反而小；②两个负数中倒数大的反而小；

③两个有理数中倒数大的反而小；④两个符号相同的的有理数中倒数大的反而小A.①②④ B.① C.①②③ D.①④

3.若 a+b<0，ab>0，则 a，b 这两个数（ ）

A.a>0，b>0 B.a>0，b<0 C.a<0，b>0 D.a<0，b<0

4.如图，A，B 两点表示的有理数分别是 a，b，则下列式子中正确的是（ ）A.ab>0 B.a−b>0 C.（a+1）（b−1）>0 D.（a−1）（b−1）>0

5.若 a  3， b  4，且 a+b<0，则 ab= .

6.已知 a，b 互为相反数，c，d 为倒数，x 的绝对值是 2，求   53

a b

a b cd x cd

   的值.

7.规定一种新运算※，两数 a，b 通过※运算得（a+2）×2−b，即 a※b=（a+2）×2−b.例如：3※5=（3+2）×2−5=10−5=5.根据上面规定解答一下题目：

（1）求 7※（−3）的值；

（2）7※（−3）与（−3）※7 的值相等吗？

45

知识点 2 有理数的除法

有理数除法法则：

1.两个有理数相除，同好得正，异号得负，并把绝对值相除

2.0 除以任何一个非 0 的数都得 0

3.除以一个数等于乘这个数的倒数

4. 0 不能作除数或者 0 不能作分母

  1

12 12 4 484

        

例题

1 下列说法正确的是（ ）

A.零除以任何数都等于零 B.1 除以一个数就等于乘这个数的倒数C.一个不等于零的有理数除以它的相反数等于−1 D.两数相除，商一定小于被除数2.下列化简：

21 1 75 6 7 1 12 1

3 7 1

7 0 25 1 63 9 36 3

6

.

.    

      

 

 ① ；② ；③ ；④；⑤，其中正确有（）A.1 个 B.2 个 C.3 个 D.4 个3.有理数 a，b 在数轴上对应点的位置如图所示，下列式子成立的是（ ）A.a>b B. a  b C. a  b  0 D. 0

a

b

练习

1.若 1

a

a  ，则 a 0，若 1

a

a   ，则 a 0.

2.计算：

（1）

1 1

2 1

12 4

   

      

    （2）    1

0 33 11

3

.        

  （3）

3 1

4 2 2

8 4  （4）  3

60 3

5

     

  （5）

3 7 5

4 8 6

   

     

    （6）   66 4

5     

 

46

3.请仔细阅读，并解答问题.两个有理数 a，b 满足 a，b 同号，求

a b

a b

 的值.解：由 a，b 同号可知，a，b 有两种可能：a，b 都是正数；a，b 都是负数. ①若 a，b 都是正数，即 a>0，b>0，有 a  a ， b  b ，则 1 1 2

a b a b

a b a b

     ；②若 a，b 都是负数，即 a<0，b<0，有 a  a ， b  b ，则 1 12a b a b

a b a b

     ；所以

a b

a b

 的值为 2 或者−2.请根据上面的解题思路解答下面的问题：

两个有理数 a，b 满足 a，b 异号，求

a b

a b

 的值.

4.对于两个有理数 a，b（b≠0），规定一种新的运算“※”：a※b=a+

1

b

.例如：1※2=1+

1

2

= 3

2 ，2※3=2+

1

3

= 7

3 ，−3※6=−3+

1

6

= 17

6  . （1）请仿照上面的例子计算下列各题：

① 3※5

②−4※3

③(1※2)※3

④1※(2※3)

（2）通过计算，请回答：

①“※”运算是否满足(m※n)※x=m※(n※x)

②当 m，n 为何值时，m※n=n※m？

47

知识点 3 有理数的乘方

n 个 a 相乘，

n

n a a  a  a  a  a 

个，底数 a，指数 n

辨别清楚底数和指数3 3  333 27

       4 3  3 33381       3 3  3 3327有理数乘方的符号法则

1. 正数的任何次幂都是正数

2. 负数的奇次幂是负数，负数的偶次幂是正数

3. 0 的奇次幂、偶次幂都是 0

2 3 3392 224               拓展

1. 任何一个有理数的偶次幂都是非负数，即 2 0

n a  （n 为正整数）

2. 若用 n 表示正整数，则 2n 表示偶数，(2n+1)表示奇数，

则(−1)

2n=1，(−1)

2n+1= −1

 

 

4

5 2 16

2 32  

  例题

1.关于式子  

4 5 ，下列说法中，错误的是（ ）

A.表示5  5 5 5 B.−5 是底数，4 是指数

C.−5 是底数，4 是幂 D.4 是指数，  

4 5 是幂

2.将式子 3 3 3 3 2 +2 +2 +2 用幂的形式表示正确的是（ ）

A.2

5 B.2

9 C.2

12 D.2

16

3.下列数或式：  

6

3 1 2 2 2 5 0 1

3

, , , ,m

      

  ，在数轴上锁对应的点一定在原点右边的个数是（）A.1 B.2 C.3 D.4

4.如果 m 为正整数，那么    

1 2 1 1 1

4

m

    m 

  的值（ ）

A.一定为零 B.一定为偶数 C.是整数但不一定是偶数 D.不能确定5.若  

2 x  2  y  3  0 ，则 x−y 的值为（ ）

A.−5 B.5 C.1 D.−1

48

6.计算

（1） 

2 4 （2）  

3 3 1  3 1 （3）   2 2 4 2  3 7 21（4）  

2 4 1

1 2 3

6       

  （5）   

2 4 3 5 2

5

      

  （6）

2

2 1 3 2 0252

.        

练习

1.下列对于  

4  3 的叙述，正确的是（ ）

A.表示−3 的 4 次幂 B.表示 4 个 3 相乘的积

C.表示 4 个−3 相乘的积的相反数 D.表示 4 个−3 相乘的积

2.下列各对数中，数值相等的是（ ）

A.−2

7与(−2)

7 B.−3

7与(−3)

7 C.2

3与 3

2 D.−(−3)

2与−(−2)

3

3.当 n 是正整数时，    

2 1 2 1 1

n n    的值是（ ）

A.2 B.−2 C.0 D.2 或−2

4.填一填：

(−1)

15= ，(−1)

16= ；( )

4=16，( )

5=32；

(−10)

5= ，( )

6=1000000.

5.计算

（1） 2 3 （2）   

2 4 3 5 2

5

      

  （3） 3 2 14 4 554     

（4） 2022 2023 0.125 8 （5）    

2

2 4 2

1 1 0 5 2 3

3

.          

 

6.当细菌繁殖时，每隔一段时间，1 个细菌就分裂成 2 个. （1）1 个细菌在分裂 n 次后，数量变为 个. （2）有一种分裂速度很快的细菌，它每 12 分钟分裂一次，如果现在盘子里有1000 个这样的细菌.① 1 小时后，盘子里有 个细菌. ② 2 小时后，细菌的数量是 1 小时后的多少倍？

49

随堂检测

1.三个数相乘，积为负数，则其中负因数的个数有 （ ）

A.1 个 B.2 个 C.3 个 D.1 个或3 个2.有 2022 个有理数相乘，如果积为 0，那么 2022 个数中（ ）

A.全部为 0 B.只有一个为 0 C.至少有一个为 0 D.有两个互为相反数3.四个有理数相乘，积的符号是负号，则这四个有理数中，正数的个数是（）A.1 个或 3 个 B.1 个或 2 个 C.2 个或 4 个 D.3 个或4 个4.一个数的偶次幂是正数，这个数是（ ）

A.正数 B.负数 C.正数或者负数 D.任何有理数5.a 是任意有理数，下列说法正确的是（ ）

A.(a+1)

2的值总是正数 B.a

2+1 的值总是正数

C.−(a+1)

2的值总是负数 D.a

2+1 的值中最大的是 1

6.在计算   5 7 2

36

12 9 3

 

     

  时，可以避免通分的运算律是（ ）

A.加法交换律 B.乘法分配律 C.乘法交换律 D.加法结合律7.若 a，b，c 在数轴上对应点的位置如图所示，则必有（ ）

A.abc>0 B.a(b−c)>0 C.(a+b)c>0 D.(a−c)b>0

8.x 是有理数，下列各式成立的是（ ）

A.  

2 2 x  x B.  

3 3 x  x C.  

3 3 x  x D.

4 4 x  x

9.计算：

（1）   1 1

3 2 2

3 3     （2）

1 1 1 7 1

3 3 7 1

7 7 3 22 21

     

 

50

（3）

4 5 1

2 1 1

7 6 21

   

      

    （4）

2 1

4

2

  

    

  

（5）   4 5

32 2

5 4

          

    （6）  

3 2 1 4 4 5 5

4

      

 

10.如果对于任意非零有理数 a，b，定义新运算⊕如下：a⊕b=(a−2b)

2÷(2a−b). （1）求(−3)⊕5 的值；

（2）求 2  5  3   的值.