遍过
学完1课,练透1课! 1课1练一遍过
九年级上册 RJ
1/5 作业册 2/5 课堂测+阶段测 3/5 培优册共5册4/5 测评卷 5/5 答案册
《一遍过》使用指南
滚动训练 分层推进·循环强化·精准突破

课堂测:课堂滚动,小步快跑


作业册:三阶滚动,层层通关

阶段测:周末滚动,循环加固


培优册·学思用
测评卷:周期检测,查漏补缺
核心知识+重难题思维建模



参考答案


第二十一章 一元二次方程
学习区 21.1 一元二次方程 过基础 过能力001
21.2解一元二次方程
课时1直接开平方法 过基础过能力003
课时2 配方法 过基础 过能力005
课时3 公式法 过基础 过能力007
课时4 因式分解法 过基础 过能力009
\*课时5一元二次方程的根与系数的关系 过基础 过能力011
拓展区 基础专项 一元二次方程的解法归纳 过专项013
培优专项 利用配方法求解最值问题 过专项014
热门专项 根的判别式的应用 过专项015
学习区 21 个
课时1传播问题、循环问题与数字问题 过基础 过能力017
课时2 平均变化率问题与销售问题 过基础 过能力019
课时3几何图形面积问题 过基础 过能力021
数学活动 过基础 023
拓展区 章末复习专练 过全章 过中考024
综合与实践(用硬纸板制作无盖纸盒) 026
反馈区·第二十一章综合能力测评卷 过综合见活页卷1
第二十二章 二次函数
学习区:22.1二次函数的图象和性质
课时1二次函数 过基础过能力027
课时2二次函数 \ y={a}x^{2} 的图象和性质·….......过基础过能力029
课时3二次函数 y=a x^{2}+k 的图象和性质…··.过基础过能力031
课时4二次函数 \scriptstyle y = a\left( x - h \right)^{ 2} 的图象和性质·过基础过能力033
课时5二次函数 γ=a\left(x-h\right)^{2}+k 的图象和性质·……过基础过能力035
课时6二次函数 \ y=a x^{2}+b x+c 的图象和性质……过基础过能力037
\*课时7用待定系数法求二次函数的解析式.过基础过能力039
微专题问题串形式
拓展区 学习区 拓展区
一题多变利用抛物线的对称性解题 041一题多变_二次函数的最值 041
热门专项求二次函数的解析式 过专项042
22.2 二次函数与一元二次方程 过基础 过能力043
基础专项 函数图象信息题 过专项045
热门专项 二次函数与线段最值问题 过专项046
热门专项 二次函数与面积最值问题 过专项047
培优专项 二次函数中的存在性问题 过专项049
\Lsh 在深度研究2022年版义务教育课程标准的基础上,天星教育研究院结合教与学实际,在《一遍过》中创设独特模块,高效解决学科痛点和难点.并通过对比分析近8课时滚动 炼出最能体现数学中考起穷的)个创新题维度:新情境、新考法、新趋势(开放题,融入数学文化、传统文化,过程性学习等)、跨学科、全面渗透核心素养.
因此,《一遍过》在紧扣教材的基础上,注重新里标理今渗透和试题的创新性,帮助学专项滚动 方法、发展素养,以适应中考新趋势
学科创新设计
过全章
在每章末,基于学生认知规律,将知识章末滚动 题多设问的方式将全草内容进行有效串联和深度融合.由点到面整合教材内容,由低到高达成学习目标,由浅入深感悟数学思想,最终获得系统性认知.如P024,P060等.
综合与实践
通过创设真实情境,以问题解决为导向,让学生从数学的角度观察与分析、思考与表达、解决与阐释社会生活以及科学技术中遇到的现实问题,体会数学的科学价值,提高发现与提出问题、分析与解决问题的能力,发展应用意识、创新意识和实践能力.如P026用硬纸板制作无盖纸盒等.
微专题
-题练透、一题多变、一图多变、数学思想、课标新增
以数学学科特有的图形、情境等鲜活生动的素材为载体,通过大小问题串的形式进行分层次、螺旋式探究,启发思路延续,促进理解掌握,构建逻辑体系,形成和发展数学思维,激发创新意识.如P041利用抛物线的对称性解题等.
课时1二次函数与图形面积问题 过基础 过能力051
课时2二次函数与最大利润问题 过基础 过能力053
课时3生活中的抛物线形问题 过基础 过能力055
数学活动· 过基础 057
拓展区: 章末复习专练 过易错过全章过中考059
综合与实践(花坛种植区域划分) 062
反馈区·第二十二章综合能力测评卷 过综合见活页卷2
一题多解
依托数学知识和方法的内在联系与多样性,鼓励学生通过不同的切入角度和不同的分析思路,多维度拆解问题,锻炼思维灵活性,引导掌握更多解题策略,提高解决问题的能力.如P006T8,P011T2,P012T11等.
学习区:23.1图形的旋转
课时1旋转的概念及性质 过基础 过能力063
课时2 旋转作图 过基础 过能力065
拓展区: 基础专项 利用旋转进行相关计算 过专项067
热门专项 旋转中的尺规作图 过专项068
培优专项 旋转中的手拉手模型 过专项069
培优专项 旋转中的半角模型 过专项070
学习区 23.2中心对称
课时1中心对称 过基础 过能力071
课时2 中心对称图形 过基础 过能力073
课时3关于原点对称的点的坐标 过基础 过能力075
23.3 课题学习 图案设计 过基础 过能力077
数学活动 过基础 078
拓展区 热门专项 旋转中的三点共线问题 过专项079
热门专项 利用旋转探究线段间的数量关系 过专项080
章末复习专练· 过全章 过中考081
反馈区·第二十三章综合能力测评卷 过综合 见活页卷3
期中综合能力测评卷 见活页卷4
课时1 圆 过基础 过能力083
课时2 垂直于弦的直径 过基础 过能力085
课时3 弧、弦、圆心角 过基础 过能力087
课时4 圆周角 过基础 过能力089
课时5 圆内接四边形 过基础 过能力091
一题练透,圆的基本性质的相关计算 093
数学思想分类讨论思想在圆中的应用 093
拓展区: 热门专项 圆中导角技巧 过专项094
基础专项与圆的性质有关的辅助线作法 过专项095
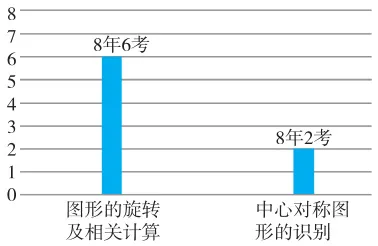
福建考点频度热力图
第二十一章一元二次方程


学习区:24.2点和圆、直线和圆的位置关系
课时1点和圆的位置关系 过基础过能力097
课时2直线和圆的位置关系 过基础 过能力099
课时3 切线的判定和性质 过基础 过能力101
课时 4 切线长定理和三角形的内切圆 过基础 过能力103
一题多变。圆与等腰三角形(母题:教材P123T4) 105
一题多变,切线性质的应用 106
拓展区 基础专项证明圆的切线的两种方法 过专项107
培优专项此时无圆胜有圆 过专项108
学习区 24.3 正多边形和圆· 过基础 过能力109
24.4 弧长和扇形面积
课时1弧长和扇形面积 过基础 过能力111
课时2 圆锥的侧面积和全面积 过基础 过能力113
数学活动 过基础 115
拓展区 培优专项 与圆有关的不规则图形面积的求法 过专项117
热门专项圆与尺规作图 过专项118
章末复习专练· 过全章过中考119
综合与实践(T1:滤纸与漏斗.T2:确定拱桥形状) 121
反馈区·第二十四章综合能力测评卷 过综合见活页卷5
第二十五章 概率初步
学习区:25.1随机事件与概率
课时1随机事件 过基础 过能力123
课时2 概率 过基础 过能力125
25.2 用列举法求概率
课时1用列表法求概率 过基础 过能力127
课时2用画树状图法求概率 过基础 过能力129
拓展区 基础专项 概率中的放回问题 过专项131
基础专项 概率中的不放回问题 过专项132
培优专项 概率与其他知识的综合 过专项133
学习区 25.3用频率估计概率 过基础 过能力135
数学活动 过基础 137
拓展区 章末复习专练· 过全章 过中考138
反馈区 第二十五章综合能力测评卷 过综合 见活页卷6
期末综合能力测评卷(一) 见活页卷7
期末综合能力测评卷(二) 见活页卷8

第二十三章旋转
第二十四章 圆

第二十五章概率初步

期末复习专题练习 见另册 《阶段滚动检测》
《单元测评卷》 单独成册:包含5套单元卷,1套期中卷,2套期末卷
21. 1 一元二次方程
过基础 教材必备知识精练
知识点1一元二次方程的概念 甄选福建九地市模拟试题和福建中考题
1[2025泉州南安期末 下列方程是一元二次方程的是
\dots x-2=0 {B}.\ x^{2}-4y=0 C.\ x^{2}-5x-1=0\qquad\qquadD.\ a x^{2}+b x+c=0
2[2025 莆田仙游期中]若方程 (a-2)x^{2}+2x+1=0 是一元二次方程,则 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 的取值范围是知识点2一元二次方程的一般形式
3[2025泉州期中]将方程 \ x^{2}+2=4x 改写成 a x^{2}+b x+c=0 的形式,则 a ,b ,c 的值分别为(
A.1,4,2 B.1,4,-2 C.~1 , -4 ,2\qquad\qquad\qquadD.~1 , -4 , -2
4教材 P4 练习 T1变式将一元二次方程 x(x-2)=5化为二次项系数为1的一般形式是,其中一次项是 ,常数项是
知识点3 一元二次方程的根 严选北京、广东等教育发达地区考题
5教材P4T7变3 [2024深圳中考]已知一元二次方程 x^{2}-3x+m=0 的一个根为 1,则 m=
6 0滚动·代数式[2025福州晋安区期中]已知方程 x^{2}-3x+1=0 有一个根是 m ,则代数式 2m^{2} 6m+2\ 026 的值为
7[2025厦门双十中学月考]若 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 是关于 x 的一元二次方程 x^{2}=3x+10 的根,求代数式 \left( a+4 \right)\left( a - 4) - 3 ( a-1 ) 的值.
精选教材变式题及其他版本教材经典原题,回归教材
知识点4 根据实际问题列一元二次方程
8教材 P4 练习 T2 变式 个菱形的两条对角线相差5,面积为12.设长对角线的长为 x ,则可列方程为
9教材P4T6 变式[2024 北京55 中月考]九年级(5)班文学小组在图书共享仪式上互赠图书,每个同学都把自己的图书给本组其他成员赠送一本,全组共送了132 本图书.若设全组共有 x 名同学,则可列方程为 (
A.x(x-1)=132 B.\;x({ x+1 })=132 \;\;\;\;\;\;\;\;\;\;\;C. (1)/(2)x({ x-1 })=132 \;\;\;\;\;\;\;\;D. (1)/(2)x({ x+1 })=132
10 传统文化
2025南平光泽期中]《中秋帖》是晋朝书法家王献之的作品,如图,在一幅长为 65\cm ,宽为 30~cm 的《中秋帖》矩形书法作品的四周镶上相同宽度的金色纸边,制成一幅矩形挂图,设金色纸边的宽为 xcm. 如果要使整个挂图的面积是 2~450~cm^{2} ,那么x 满足的方程是
过能力
学科关键能力构建
11[2024三明三元区期中]下表是代数式 a x^{2}+b x 的值的情况,根据表格中的数据,可知方程 a x^{2}+ b x=6 的根是 (
| x | · | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
| 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 |
A.0,1 B.-1,2 C.-2,3 D.-3,4
12[2025三明尤溪月考]若关于 x 的一元二次方程 a x^{2}+b x+2=0( a {\ne}0 ) 有一根为2 024,则关于 x 的一元二次方程 a\left( x-1 \right)^{ 2}+b x-b+2=0 必有一根为 )
B.2 024 C.2 025数学文化[2024龙岩二中月考]《九章算术》中“勾股”章有一题:“今有户高多于广六尺八寸,两隅相去适一丈,问户高、广各几何?”大意是说:“已知有一扇长方形门的高比宽多6尺8寸,门的对角线长为1丈,那么门的高和宽各是多少?”如果设门的宽为 x 尺,那么可列方程为· (1 丈 =10 尺 ,1尺 =10 寸)
素养提升
抽象能力[2024 厦门湖里实验中学月考]如图,四边形 ACDE是证明勾股定理时用到的一个图形, a ,b ,c 是 Rt \triangle A B C 和 Rt\triangle B E D 的边长,易知 A E={√(2)} c ,这时我们把关于 x 的形如 a x^{2}+√(2) c x + b=0 的一元二次方程称为“勾系一元二次方程”,比如 3x^{2}+5 √(2) x +4=0 是“勾系一元二次方程”.请解决下列问题:
(1)方程 x^{2}+2x+1=0 “勾系一元二次方程”(填“是”或“不是”);
(2)若-1是“勾系一元二次方程” a x^{2}+{√(2)} c x+b=0 的一个根,且四边形ACDE 的周长是12,求\triangle A B C 的面积.

素养提升题:符合新课标趋势,渗透数学核心素养
21.2 解一元二次方程
课时 1 直接开平方法
过基础
教材必备知识精练
答案P6
知识点1 解形如 x^{2}=p(p>=slant0) 的一元二次方程
1[2025莆田仙游期中]方程 x^{2}=1 的根为
A. x=1 B.\ x=-1 \operatorname{C}. x=±1 D. x=±2
2[2025 福州福清期中]方程 x^{2}-4=0 的根是
A. x_{1}=x_{2}=2 B.\ x_{1}=x_{2}=√(2)\qquad\qquadC.\ x_{1}=2 ,x_{2}=~-2~\qquad~D.~x_{1}=√(2) ,x_{2}=~-√(2~)
3[2024福州月考]若2是关于 x 的方程 x^{2}-c=0 的一个根,则这个方程的另一个根是
A.-2 \mathbf{B}. √(2 ) C.2 D. 4
4 用直接开平方法解下列方程:
( 1 ) 2x^{2}=18 ; ( 2 )9x^{2}-6= - 1 ; ( 3 )36x^{2}-81=0.
知识点2 解形如 \left( m x+n \right)^{2}=p\left( p>=slant0 \right) 的一元二次方程
5[2024厦门月考]一元二次方程 \left( x+1 \right)^{2}=16 用直接开平方法可转化为两个一元一次方程,其中一个一元一次方程是 x+1=4 ,则另一个一元一次方程是 (
B.\ x-1=4\qquad\qquad\qquadC.\ x+1= -4 C.~x+1=~-~4\qquad\qquadD.~x+1=4
6[2025宁德-中月考]方程 \left( x-2 \right)^{2}=9 的根是
A. x_{1}=5 ,x_{2}=1 B.\ x_{1}=3 ,x_{2}=\ -3\qquad~C.\ x_{1}=5 ,x_{2}=\ -1\qquad~D.\ x_{1}=11 ,x_{2}=\ -7
7[2024 福州屏东中学期中]若关于 x 的方程 \left( x-2 \right)^{2}=m+1 有实数根,则 m 的取值范围是()
A. m>1 B.\ m>-1 C.\ m>=1 \operatorname{D.} m>=-1
8开放题若关于 x 的一元二次方程 \left(x+3\right)^{2}=c 有实数根,则 c 的值可以为 ·(写出一个即可)
9 教材 P6 练习变式解下列方程:
(1) \left( x+3 \right)^{2}-8=0 ; (2) \mid\left( 2x-1 \right)^{2}-121=0 ;
( 3 ) 8 ( x-3 )^{ 2} -72=0 ; \left(4\right)x^{2}-10x+25=64.
过能力
学科关键能力构建
课时滚动:巩固新题基础,唤醒旧知
10滚动·实数 1, x_{2} 是一元二次方程 \left(x-1\right)^{2}=5 的两个根,且 x_{1}<x_{2} ,下列说法正确的是
A. x_{1} 小于 - 1 ,x_{2} 大于3 B. x_{1} 小于 - 2 ,x_{2} 大于3
C. x_{1} ,x_{2} 在-1和3之间 D. x_{1} ,x_{2} 都小于3
11[2024 泉州南安期中]现在定义一种运算,其规则为 a*b=a^{2}-b^{2} ,根据此规则,如果 x 满足 2\left( x +
2) * 5 = - 1 ,那么 x 的值为 )
A. - 2+{√(6)} B.~-2+2√(6~)\qquad\qquadC.~-2±√(6~)\qquad\qquadD.~-2±2√(6~)\qquad\qquadC.~-2±2√(6~)\qquad\qquadD.~-2±2√(6~)
12[批判性思维下列是小明解方程 \scriptstyle\left(\;x\;-\;1 \right)^{\;2}\;=\;4\left(\;x\;-9 \right)^{\;2} 的过程.
解: x-1=2\left( x-9 \right) 第一步x-1=2x-18 , 第二步解得 x=17 第三步(1)以上解方程的过程中从第 步开始出现错误,错误的原因是(2)请将这个方程正确的求解过程填写在下列框图中★素养提升

13[抽象能力[2024 三明尤溪期中]综合与实践:阅读材料,并解决以下问题.
(1)学习研究:北师大版教材九年级上册第39页介绍了我国数学家赵爽在其所著的《勾股圆方图注》中关于一元二次方程的几何解法,以 x^{2}+2x-35=0 为例,求解过程如下.① 变形:将方程 x^{2}+2x-35=0 变形为 x(x+2)=35 :② 构图:画四个长为 x+2 ,宽为 x 的矩形,按如图1所示构造一个“空心”大正方形;③ 解答:图中大正方形的面积从整体看可表示为 \left( x +x +2 \right)^{ 2} ,从局部看还可表示为四个矩形与中间小正方形面积之和,即 4x\(\;x+2\;)\;+2^{2}=4x35\;+4=144 ,因此,可得新的一元二次方程\left( x+x+2 \right)^{2}=144.\because x 表示边长, \therefore2x+2=12 ,即 x=5 这种数形结合方法虽然只能得到原方程的其中一个正根,但是从新方程 \left( x+x+2 \right)^{2}=144 可以得到原方程的另一个根是
(2)类比迁移:根据赵爽几何解法的方法求解方程 x^{2}-3x-4=0 的一个正根(写出完整的求解过程,并在图2 中画出示意图、标明各边长).


课时 2 配方法
过基础
教材必备知识精练
答案P6
知识点1 配方的概念
华师九上教材P27T1填空,将左边的多项式配成完全平方式:
\begin{array}{l}{{\displaystyle(\ 1\ )\ x^{2}\ +6x\ +\ \ \ \ \ \ \ \ }}\\ {{\displaystyle(\ 3\ )x^{2}\ +(3)/(2)x\ +\ \ \ \ \ \ \ }}\end{array} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array}{l}{{\displaystyle(\ 2) x^{2}\ -8x\ +\ \ \ \ \ \ \ \ }}\\ {{\displaystyle(\ 3) x^{2}\ +(3)/(2)x\ +\ \ \ \ \ \ \ \ }}\end{array}\ \ ,\ \ \ \ \ \ \ \ \ \ \ \ \begin{array}{l}{{\displaystyle(\ 3\ ) x^{3}\ +6x\ +\ \ \ \ \ \ \ \ \ \ }}\\ {{\displaystyle(\ 4)4x^{2}\ -6x\ +\ \ \ \ \ \ \ \ \ \ }}\end{array}\ \ \ \ \ \ \ \ \ \ \ \begin{array}{l}{{\displaystyle=(\ x-\ 1\ )^{2} ;}}\\ {{\displaystyle=\ d (\ x-\ 1)^{2} + 2(x-\ 1)^{2}\ .}}\end{array} (2x-_)².
知识点2 用配方法解二次项系数为1的一元二次方程
2[2025 泉州期末]用配方法解一元二次方程 x^{2}+2x-3=0 ,下列变形正确的是
3[2024 福州文博中学期中]将一个关于 x 的一元二次方程配方为 \left( x +m \right)^{2}=p ,若 2±{√(3)} 是该方程的两个根,则 m 的值是
4 用配方法解下列方程:
\left( 1 \right)x^{2}-2x=8 ; ( 2 ) x^{2}+{(2)/(3)}x+1=0 ; (3 ) x ( x+7 ) =4x -1.
知识点3 用配方法解二次项系数不为1的一元二次方程
5[批判性思维[2025莆田第十五中学月考]王明在学习了用配方法解一元二次方程后,解方程 2x^{2} 8x+3=0 的过程如下:解:移项,得 2x^{2}-8x=\mathbf{α}-3 第一步二次项系数化为1,得 x^{2}-4x= - 3 第二步配方,得 x^{2}-4x+4=-3+4 , 第三步即 \left( x-2 \right)^{2}=1 第四步由此可得 x-2=1 或 x-2=-1 , 第五步解得 x_{1}=3 ,x_{2}=1 .· 第六步(1)王明的解题过程从第 步开始出现了错误,错误原因是(2)请利用配方法正确地解方程: 2x^{2}-8x+3=0
中考新趋势题:批判性思维、过程性学习、开放题、 跨学科试题等
知识点4 配方法的应用
6[2024 泉州南安期中]关于代数式 - x^{2} -2x + 3 的最值,下列说法正确的是
A.有最小值,是4 B.有最大值,是4 C.有最小值,是8 D.有最大值,是8
7[2025厦门槟榔中学月考]若 M=x^{2}-8x+11 , N=2x^{2}-12x+15 ,则 M 与 N 的大小关系为()
A. M{>=slant}N B. M>N C. M{<=slant}N D. M<N
过能力
学科关键能力构建
答案 P6
8[一题多解[2024三明期中]已知方程 x^{2}-4x+1= ,等号右侧的数印刷不清楚.若可以将其配方成 \left( x-m \right)^{2}=5 的形式,则印刷不清楚的数是 (
A. -3 B.-2 C.3 D.2
9[2024 随州期中]在实数范围内定义运算“☆”和“ \star ”,其规则为 a \underset{\rightharpoondown}{\star} b=a^{2}+b^{2} ,a\star b=(a b)/(2) ,则方程3☆ x=x\star12 的根为
10 用配方法解下列方程:
( 1 )(1)/(2)x^{2}-6x -7=0 ; \begin{array}{c c}{{\left(2\right)\left(2x-3\right)\left(2x-1\right) =5 ;~~~~~~}}&{{~~~~~~~(3\right)3x^{2}+6√(2) x-1=0.}}\end{array}
素养提升
11 应用意识阅读下列材料:
早在公元1世纪左右,我国著名的数学典籍《九章算术》中就已经对一元二次方程进行了研究:在“勾股”章中,根据实际问题列出方程 x^{2} +34x -71\ 000=0 ,给出该方程的正根为 x=250 并简略指出解该方程的方法一开方除之.其后,受此启发,有数学家研究了利用几何图形求解该方程的方法,对于丰富我国古代有关一元二次方程的研究具有重要的价值.用该方法求解的过程如下(如图):
第一步:构造
已知小正方形的边长为 x ,将其边长增加17,得到大正方形.

第二步:推理
根据图形中面积之间的关系,可得 \left( x+17 \right)^{2}=x^{2}+2x17x+17^{2}
由原方程 x^{2}+34x-71\ 000=0 ,得 x^{2}+34x=71\ 000
所以 ( x+17 )^{ 2}=71~000+17^{ 2}
所以 ( x+17 )^{ 2}=71\ 289
直接开方可得正根 x=250
依照上述解法,要解方程 x^{2}+b x+c=0( b>0 ) ,请写出第一步“构造”的具体内容:
与第二步中“ \left( x+17 \right)^{2}=71\ 000+17^{2}* ”相应的等式是
课时3 公式法
过基础
教材必备知识精练
答案P6
知识点1 根的判别式
1[2023吉林中考]一元二次方程 x^{2}-5x+2=0 根的判别式的值是
A.33 B.23 C.17 D.\ √(17)
2[2024 北京中考]若关于 x 的一元二次方程 x^{2}-4x+c=0 有两个相等的实数根,则实数 c 的值为( )
A.-16 B. -4 C.4 D.16
3[2025漳州南靖期中]若关于 x 的一元二次方程 x^{2}-2x-m=0 无实数根,则 m 的取值范围为()
A. m>-1 B.\ m>1 C.\ m>=slant-1\qquad\qquad\qquadD.\ m>=slant-1
4[易错题[2025福州第十二中学开学]若关于 x 的一元二次方程 k x^{2}+4x-2=0 有实数根,则 k 的取值范围是 )
A. k>=-2 B.\ k>-2 且 k\neq0 C. k≥-2且k≠0 D. k≤- 2
5下列方程中,有两个不相等的实数根的是
A. x^{2}=0 B.\ x^{2}-3x-1=0\qquad\quadC.\ x^{2}-2x+5=0\qquad\qquadD.\ x^{2}+1=0
6[教材 P17T4 变式不解方程,直接判断下列一元二次方程的根的情况
\left( 1 \right)x^{2}-3x-7=0 ; (2 )9x^{2}+6x+1=0 ;\qquad\qquad\qquad(3 )2x^{2}-5x+4=0.
7代数推理|华师九上教材P33T2小明告诉同学,他发现了判断一类方程有无实数根的简易方法:若一元二次方程 a x^{2}+b x+c=0\left( a {\ne}0 \right) 的系数 a,c 异号(即两数为一正一负),那么这个方程一定有两个不相等的实数根.他的说法是否正确?为什么?
知识点2 用公式法解一元二次方程
8[2024 厦门实验中学期中]x=-3±√3²-4x2×1 是下列哪个一元二次方程的根?
\Lsh 用公式法解下列方程:
\left( 1 \right)x^{2}-3x-2=0 ; \left( 2 \right)x^{2}-2 √(2) x +2=0 ; ( 3 ) -3x^{2}+5x+2=0.
过能力
学科关键能力构建
答案P6
10[2025 福州七中月考]定义运算; m\*\tilde{\ll} n=m n^{2} -m n -1 ,例如 4x2=4x2^{2}-4x2-1=7 ,则方程
2☆ x=0 的根的情况为 ( )
A.有两个不相等的实数根 B.有两个相等的实数根C.无实数根 D.只有一个实数根
11代数推理[2025 福州一检]已知 x_{0} 是一元二次方程 a x^{2} +b x +c=0 ( a \ne0 ) 的实数根, \Delta={b}^{2}~-~ 4a c. 设 M=\left( 2a x_{0}+b \right)^{2} ,则下列判断正确的是 ()
A. 2M=\Delta B.\ {\cal M}=2\Delta\qquad\qquad\qquadC.\ {\cal M}-\Delta=0 C.~M-\varDelta=0~~~~~~~~~~~~~~~~~~~D.~M+\varDelta=0
12[开放题[2023杭州中考]设一元二次方程 x^{2}+b x+c=0. 在下面的四组条件中选择其中一组 b ,c 的值,使这个方程有两个不相等的实数根,并解这个方程.
13 已知关于 x 的一元二次方程 x^{2}+k x-4k-16=0
(1)试判断这个方程的根的情况
(2)是否存在实数 k ,使这个方程的两个根为连续偶数?若存在,求出 k 的值及方程的根;若不存在,请说明理由.
素养提升
14推理能力|开放题[2024厦门大同中学月考]有四组一元二次方程: ①x^{2}-4x+3=0 和 3x^{2}-4x+ 1=0 , ②x^{2}-x-6=0 和 6x^{2}+x-1=0 ③x^{2}-4=0 和 4x^{2}-1=0 , ④4x^{2}-13x+3=0 和 3x^{2}~-~ 13x+4=0. .这四组方程具有共同特征,我们把具有这种特征的一组一元二次方程中的一个称为另一个的“相关方程”.请写出一个有两个不相等的实数根但没有“相关方程”的一元二次方程:
课时4 因式分解法
过基础
教材必备知识精练
答案P6
知识点1 用因式分解法解一元二次方程
1【易错题[2025泉州晋江期末]一元二次方程 x^{2}=2x 的根是
A. x=0 \mathbf{B}.\ x=2 C.\ x_{1}=x_{2}=2\qquad\qquadD.\ x_{1}=0 ,x_{2}=2
2[2025 泉州南安期中]已知一元二次方程的两根分别为 x_{1}=1 ,x_{2}= - 3 ,则这个方程可以为()
3[2024 漳州长泰-中期中]嘉嘉在解方程 x( x-3 )=x-3 时,只得到一个解是 x=1 ,则他漏掉的解是 (
A. x=3 \operatorname{B}.\ x=-3 C, x=0 D.\ x=-1
教材P14T1变式用因式分解法解下列方程:
(1)4x^{2}+11x=0;\qquad\quad(2)x(x+3)=2x;\qquad\quad(3)2x^{2}+8=8x; (4)9(x+1)² -(2x -5)²=0.
5批判性思维以下是某同学解方程 x^{2}-3x=-2x+6 的过程:
解:方程两边因式分解,得 x( x-3 ) = - 2 ( x-3 ) ,{D}
方程两边同除以 \left( x-3 \right) ,得 x=- 2 ②
原方程的根为 x= - 2. ③
(1)上面的运算过程中,第 步出现了错误. (填序号)
(2)请你写出正确的解答过程
知识点2 用适当的方法解一元二次方程
6 用合适的方法解下列方程:
( 1 )2 ( x-3 )^{ 2}=8 ;\qquad( 2 ) x^{2} +4x= -3 ; ( 3 )4x^{2}-6x-3=0 ; (4)(2x -1)²=9(1 -2x).
过能力
答案P6
7[2025泉州永春三中期中]对于实数 a ,b ,定义新运算,规则如下: a\triangle b=b^{2}-a b ,则等式 6 \triangle x=7 中 x 的值为 )
A.1或-7 B.-1或7 C.-1 D.-7
8滚动·三角形[2025厦门双十中学期中]已知关于 x 的一元二次方程 \left( a + b \right)x^{2} +2c x + ( b - a ) =0 ,其中 a ,b ,c 分别为 \triangle A B C 三边的长.
(1)如果 x=-1 是方程的根,试判断 \triangle A B C 的形状,并说明理由;(2)如果 \triangle A B C 是等腰直角三角形, c 为斜边,解这个一元二次方程
9[2025 泉州晋江-中期中]阅读材料:解方程 x^{2}+2x-35=0 ,我们可以按下面的方法解答:
| (1)分解因式:x²+2x-35. ①竖分二次项与常数项:x =x·x,-35=(-5)×(+7). ②交叉相乘,验中项: 7x-5x=2x +7 ③横向写出两因式:x²+2x-35=(x-5)(x+7). | (2)若ab=0,则α=0或b=0,:.方程x²+2x -35=0可以这样求解: 分解因式,得(x-5)(x+7)=0, .x-5=0或x+7=0, .x=5,x2=-7. |
上述这种解一元二次方程的方法叫作十字相乘法.请参考以上方法解下列方程:
\left( 1 \right)x^{2}+5x+4=0 ; (2)2x^{2}+x-10=0.
素养提升
10「抽象能力阅读:我们可以用换元法解简单的高次方程,解方程 x^{4}-3x^{2}+2=0 时,可设 \ y=x^{2} ,则原方程可化为 y^{2}-3y+2=0 ,解得 y_{1}=2 ,y_{2}=1 当 γ=2 时, x^{2}=2 ,所以 x_{1}={√(2)}\;,x_{2}=\;- {√(2)} ;当 γ=1 时, x^{2}=1 ,所以 \l_{,x_{3}}=1 ,x_{4}= - 1 ,故原方程的根为 x_{1}=√(2)\;,x_{2} = - √(2)\;,x_{3} =1\;,x_{4} = - 1. 仿照上述方法解答下列问题
(1)已知方程 ( 2x^{2}+1 )^{ 2}+2x^{2}-3=0 ,设 γ=2x^{2}+1 ,则原方程可化为(2)解方程: \begin{array}{r}{\left(\;x^{2}-2x+1\;\right)^{2}+2x^{2}-4x-1=0.}\end{array}
课时5 一元二次方程的根与系数的关系
过基础
教材必备知识精练
答案P6
知识点1 一元二次方程的根与系数的关系
1[2025 漳州龙海区期中]设方程 x^{2}+x-2=0 的两个根为 α ,β ,那么 α+β+αβ 的值等于()
A.-3 B.-1 C.1 D.3
2一题多解若-1是方程 x^{2}+x+m=0 的一个根,则此方程的另一个根是
变式题 多角度考查同一知识点 C.1 D.2 \bullet
3[2025 南平武夷山第-中学月考]若方程 x^{2}+8x-4=0 的两个根分别为 x_{1} ,x_{2} 则 \overline{{{(1)/(x_{1)}}+{(1)/(x_{2)}}}} 的值为(
B.2 C. {(1)/(2)} D.-2
[变式][2025泉州六中期中]已知 m ,n 是一元二次方程 x^{2}+3x-1=0 的两个根,则 \left( m+1 \right) \stackrel{.}{n}+ 1)的值为 )
A.-3 B.3 C.1 D.-1
[变式2[2023乐山中考]若关于 x 的一元二次方程 x^{2}-8x+m=0 的两根为 x_{1} ,x_{2} ,且 x_{1}=3x_{2} ,则 m 的值为 )
A.4 B.8 C.12 D.16
4 [2025 漳州立人学校期中]已知关于 x 的一元二次方程 x^{2}-6x+k+1=0 的两个实数根是 x_{1} ,x_{2} ,且 x_{1}^{2}+x_{2}^{2}=24 ,则 k 的值是 )
B.-7 C.6 D.5
5「易错题下列一元二次方程中,两根之和为2的是
A. 2x^{2}-4x+1=0 \begin{array}{l}{{B.\;x^{2}+2x-1=0}}\\ {{D.\;x^{2}-5x+2=0}}\end{array} \operatorname{C}. x^{2}-2x+3=0
6[2024 福州文博中学期中]若关于 x 的一元二次方程 x^{2} + ( k -2 ) x -1 =0 的两实数根互为相反数,则 k 的值为
7[苏科九上教材 P22 尝试与交流小明在一本课外读物中读到如下一段文字:一元二次方程 x^{2}- x =0 的两根是 2+{√(3)} 和 2-{√(3)} 你能写出这个方程中被墨迹污染的一次项系数和常数项吗?
过能力
答案 P6
8[2025漳州南靖期中]若 x_{1} ,x_{2} 是方程 x^{2}-4x-7=0 的两个实数根,则代数式 x_{1}^{2}-2x_{1}+2x_{2} 的值为 )
A.7 B.12 C.14 D.15
9[2025 泉州泉港区期末]在解一道一元二次方程题时,因印刷不清楚,小影在解题过程中仅看错了常数项,解得方程的两个根是6和1;小冬仅看错了一次项的系数,解得方程的两个根是-2和-5,则原来的方程可能是 ()
10关于 x 的方程 \left( x-1 \right)\left( x+2 \right) =p^{2}\left( p\right) 为常数)的根的情况,下列结论中正确的是
A.两个正根 B.一个正根,一个负根C.两个负根 D.无实数根
11滚动·二元一次方程组|一题多解已知关于 x 的一元二次方程 x^{2}-2x-3m^{2}=0
(1)求证:方程总有两个不相等的实数根; (2)若方程的两个实数根分别为 α,β ,且 α+2β=5 ,求 m 的值
12 0滚动·勾股定理[2025 厦门外国语瑞景分校期中]已知关于 x 的一元二次方程 x^{2}+a x-a-1=0.
(1)求证:不论 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 取何值,该方程总有两个实数根;
(2)若 Rt△ABC 的两条直角边 A B,A C 的长恰好是该方程的两个实数根,且斜边长 B C 的长为 *√(5) , 求 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 的值.
★素养提升
13[推理能力[2025漳州期末]已知实数 m ,n 满足 m^{2}+b m+4=0 ,n^{2}+b n+4=0 ,且 m\neqn
(1)试说明: b^{2}-16 的值恒为正数;(2)求证: {(1)/(m^{2)}}+{(1)/(n^{2)}}>{(1)/(2)}.
见另册 《阶段滚动检测》
本节上完请使用阶段滚动检测
利用抛物线的对称性解题
1[母题[2025 福州期中]已知抛物线 y=a x^{2}+b x+c ,y 与 x 的部分对应值如表所示,下列说法错误的是
| X | -1 | 1 | 2 | 3 | |
| y | 0 | 3 | 4 | 3 | m |
A.开口向下 B.顶点坐标为(1,4)C.当 x<1 时, \boldsymbol{y} 随 x 的增大而减小 D. m=0
2[求对称轴|一题多解[2025北京西城区期中]二次函数 y=\left( x-5 \right)\left( x+7 \right) 的图象的对称轴是
A.直线 x=-1 B.直线 x=1 C.直线 x=2 D.直线 x=6
3求与 x 轴的交点坐标[2025 武汉月考]如图,抛物线 y=a x^{2}+b x+c\left( a\neq0 \right) 的对称轴为直线 x=1 ,与 x 轴的一个交点坐标为(-1,0),则 9a+3b+c 的值为

4[比较函数值的大小[2025 福州十九中月考]已知二次函数 y=\left| a \right|x^{2}-2\left| a \right|t x+c\left( a \ne0 \right) 上有两点A\left( x_{1} ,y_{1} \right),B\left( x_{2} ,y_{2} \right) ,当 1<x_{1}<2 ,2<x_{2}<3 时,总有 y_{1}<y_{2} ,则 t 的取值范围是
一题多变
答案 P21
二次函数的最值
1母题已知函数 y=2x^{2}-4x-3 ,当 2<=slantx<=slant3 时,该函数的最大值是
A.-5 B.3 C. -3 D. 5
2[由函数的最值求函数中待定字母的值[2025 泉州丰泽区月考]当 - 2<=slant x<=slant1 时,二次函数 γ = -\left( x-m \right)^{2}+5 有最大值4,则实数 m 的值为 (
A.-3 B.-1或2 C.2或-3 D.2或-3或-1
3【由函数的最值求字母的取值范围[2025 宁波期中]若二次函数 y=x^{2}+2x-3\left( m<=slantx<=slant2 \right) 有最小值-4,最大值5,则 m 的取值范围是
22.2 二次函数与一元二次方程
过基础 教材必备知识精练
答案P6
知识点1 二次函数与一元二次方程的关系
1[2024 北京海淀区期末]在平面直角坐标系 x O y 中,抛物线 y=a x^{2}+b x+c {\bigl(} a \not= 0)如图所示,则关于 x 的方程 a x^{2}+b x+c=0 的根的情况是
A.有两个不相等的实数根 B.有两个相等的实数根C.有实数根 D.没有实数根
2[2025厦门莲花中学月考]二次函数 γ=x^{2}-2x+1 的图象与 x 轴的交点个数是
A.0 B.1 C.2 D.不能确定

3教材 P47T6变式如果 a<0 ,抛物线 \ y=a x^{2}+b x+c 的顶点在第二象限,则方程 \;a x^{2}\;+\;b x\;+\;c=0 的实根情况是 )
A.有两个不相等的实数根 B.有两个相等的实数根C.无实数根 D.以上三种均有可能
4[2025北京海淀区期中]如图,在平面直角坐标系 x O y 中,抛物线 \ y=a x^{2}+b x+c 的对称轴为直线 x=2 ,与 x 轴的一个交点为(1,0),则关于 x 的方程 a x^{2}+b x+ c=0 的解为
知识点2 利用二次函数的图象求一元二次方程的近似根

5[2025莆田擢英中学月考]如下表是二次函数 \ y=a x^{2}+b x+c 的自变量 x 与函数值 \boldsymbol{y} (精确到0.01)的部分对应值,据此判断方程 a x^{2}+b x+c=0(a\neq0,a,b ,c 为常数)的一个根 x 所在的范围是()
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.06 |
A. 6<x<6. 17 B.\ 6.\ 17<x<6.\ 18 C. 6. 18 <x <6. 19 D. 6. 19 <x <6. 20
知识点3 二次函数与不等式的关系
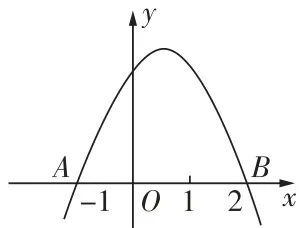
6[2025 杭州月考]如图,抛物线 y=a x^{2}+b x+c\big( a \ne0 \big) 与 x 轴的两个交点分别为 A(\mathit{\Pi}-1 ,0) 和 B(2,\ensuremath{0}) ,当 γ<0 时, x 的取值范围是 ( )
A. x<-1 B. x<-1 或 x>2 C. -1<x<2 D. x>2

7如图,直线 \ y=m x+n 与抛物线 \ y=a x^{2} + b x + c 交于 A{\bigl(} -1 ,p {\bigr)} ,B{\bigl(} 4 ,q {\bigr)} 两点,则关于 x 的不等式m x+n<a x^{2}+b x+c 的解集是
过能力
学科关键能力构建
答案P6
8[2025 洛阳质检]二次函数 \ y={a x}^{2}+b x 的图象如图.若关于 x 的一元二次方程 \;a x^{2}+b x=m 有实数根,则 m 的取值范围为 ( )
A. m>=slant-3 B. m≤ -3 C. m>{-3} D .\ m<-3


9[2025厦门三中月考]如图,以(1,-4)为顶点的抛物线 \ y=a x^{2}+b x+c 与 x 轴负半轴交于 A 点,则 一元二次方程 a x^{2}+b x+c=0 的正数解的范围是 )
A. 2<x<3 {B}.\ 3<x<4 C.\;4<x<5\qquad\qquadD.\;5<x<6
10[2025 龙岩上杭期中]已知关于 x 的一元二次方程 \left( x -m \right)^{2} +n=0 的解为 x_{1}=2 ,x_{2}=5 ,则抛物线 y=\left( x-m+2 \right)^{2}+n 与 x 轴的交点坐标是 )
A.(2,0),(5,0) B.(4,0),(7,0) ~C.~(2 ,0) ,(3 ,0)\qquad\quad~D.~(0 ,0) ,(3 ,0)
11[2025北京八十中期中]二次函数 y=x^{2} -4x + c 满足以下条件:当 3<x<4 时,它的图象位于x 轴的下方;当 4<x<5 时,它的图象位于 x 轴的上方,则 c 的值为
12易错题已知函数 y=m x^{2}+\left( 2m-1 \right)x+m\big( m 为常数)的图象与 x 轴只有一个公共点,求 m 的值.
素养提升
13[推理能力[2025西安月考]已知抛物线 \ y=a x^{2}+b x+c 上的部分点的横坐标 x 与纵坐标 \boldsymbol{y} 的对应值如表:
| x | - 4 | -3 | -2 | -1 | 0 | ||
| y | -3 | m | 1 | 0 | -3 |
以下结论: ① 该抛物线的开口向上; ② 对称轴为直线 style x= - 2 ;{③} 关于 x 的方程 \;a x^{2}\;+\;b x + c=0 的根为-1和-3; ④ 当 γ<0 时, x 的取值范围是 - 3<x< - 1. .其中正确的有 )
A.1个 B.2个 C.3个 D.4个
基础专项 函数图象信息题
100 过专项 阶段强化专项训练
答案 P6
方法指导
1.根据抛物线开口方向判断 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} :开口向上, a>0 ;开口向下, a<0
2.由 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 和对称轴的位置判断 b :规律是“左同右异”,即对称轴在 \boldsymbol{y} 轴左侧, a ,b 同号;对称轴在 \boldsymbol{y} 轴右侧, a ,b 异号.
3.由抛物线与 \boldsymbol{y} 轴的交点位置判断 c :交于正半轴, c>0 ;交于负半轴, c<0 ;交于原点, c=0
4.特殊式子的判断:看到 a+b+c ,令 x=1 ;看到 a-b+c ,令 x=-1 ;看到 4a+2b+c ,令 x=2 ;看 到 4a-2b+c ,令 * x=-2 ,然后看纵坐标.
5.根据- -{(b)/(2a)}>1 或 -{(b)/(2a)}<1 判断 2a+b 的符号;根据 -{(b)/(2a)}>-1 >-1或- -{(b)/(2a)}< -1 判断 2a-b 的符号。
6.知道抛物线 y=a x^{2}+b x+c\big( a\neq0 \big) 与 x 轴的交点情况,可得 \Delta=b^{2}-4a c 与0的大小关系.
类型1 函数图象共存问题
1一题多解[2025泉州七中月考]在同一平面直角坐标系中,一次函数 \ y=\ - m x +n^{2} 与二次函数 y= x^{2}+m 的图象可能是
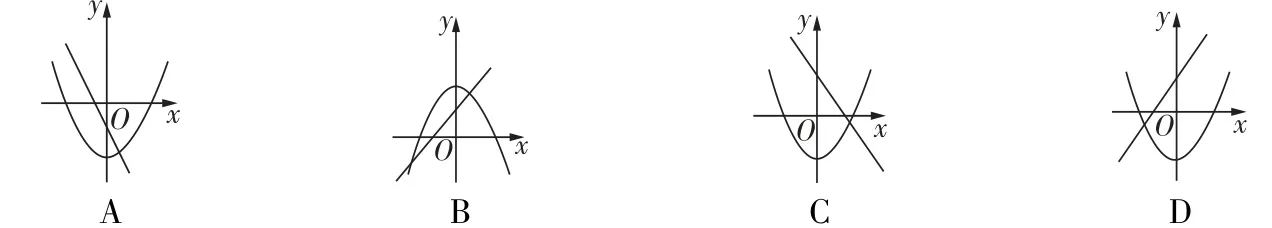
2[2025苏州振华中学期中]二次函数 γ=a\big( x-3 \big)^{ 2} +c 与一次函数 γ=c x+a 在同一平面直角坐标系中的大致图象可能是 (

类型 2 二次函数图象与 a ,b ,c 之间的关系
3[2025福州延安中学月考]如图,二次函数 \ y=a x^{2} + b x + c 的图象与 x 轴交于A(-2,0), B 两点,对称轴是直线 x=2 ,下列结论中,所有正确结论的序号为){1}a>0 ② 点 B 的坐标为(6,0); ③c=3b : ④ 对于任意实数 m ,都有 4a+2b>=slant a m^{2}+b m.
A. ①② B. (2)\widehat{(3)}\qquad\qquad\qquadC. (2)\widehat{(3)\widehat{(4)}} D.③④
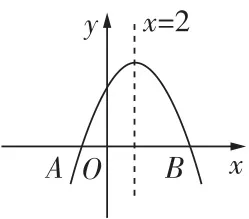
4[2024 泰安中考]如图是二次函数 y=a x^{2} +b x +c ( a\neq0 ) 的部分图象,该函数图象的对称轴是直线 x=1 ,图象与 \boldsymbol{y} 轴交点的纵坐标是2.有下列结论: {\scriptsize{~underline{~{1~}}}}2a+b=0 ② 方程 a x^{2}+b x+c=0 一定有一个根在-2 和-1 之间; ③ 方程 a x^{2}+b x+c-{(3)/(2)}=0 一定有两个不相等的实数根; \circled{4}b-a<2. .其中,正确结论的个数是 ()
热门专项 二次函数与线段最值问题
过专项 阶段强化专项训练
答案P6
方法指导
1.求斜线段 M P ,竖直线段 N P 长的最值的步骤(如图):① 设点 P( t ,a t^{2}+b t+c ) ,M( p ,m p+n )\;,N( t ,m t+n ) :② 表示线段 M P ,N P 的长: M P^{2} = \left( t -p \right)^{2} + \left( a t^{2} +b t +c -m p -n \right)^{2} ,NP =a t^{2}+b t+c-m t-n ; ③ 化简 M P,N P ,利用二次函数的性质求最值.

2.求线段之和(周长)最小:根据二次函数图象的对称性,作对称点,结合“将军饮马”模型求最值。
3.求线段之差最大:将两定点转化到定线的同侧,当两定点与动点共线时,线段之差最大.
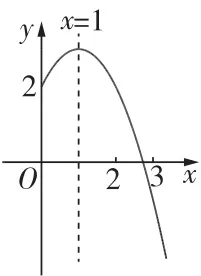
1[2024 内蒙古中考节选]如图,在平面直角坐标系中,二次函数 y=a x^{2}+b x+c\left( a\neq0 \right) 的图象经过原点和点 A(4,0) ·经过点 A 的直线与该二次函数图象交于点 B( 1 ,3 ) ,与 \boldsymbol{y} 轴交于点 C
(1)求二次函数的解析式及点 C 的坐标
(2)点 P 是二次函数图象上的一个动点,当点 P 在直线 A B 上方时,过点 P 作 P E\perp x 轴于点 E ,与直线 A B 交于点 D ,设点 P 的横坐标为 m ,则当 m 为何值时线段 P D 的长度最大,并求出最大值.
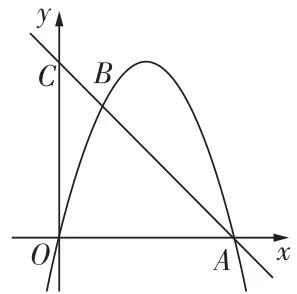
2[2024 宜宾中考节选]如图,抛物线 \ y=x^{2} + b x + c 与 x 轴交于点 A\left(\mathbf{\varepsilon}-1 ,0\right) 和点 B ,与 \boldsymbol{y} 轴交于点 C(0 , -4 ) ,其顶点为 D
(1)求抛物线的解析式及顶点 D 的坐标
(2)在 \boldsymbol{y} 轴上是否存在一点 M ,使得 \triangle B D M 的周长最小?若存在,求出点 M 的坐标;若不存在,请说明理由.
热门专项 二次函数与面积最值问题
过专项
阶段强化专项训练
答案 P6
方法指导
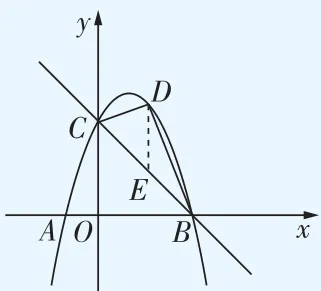
1.铅垂法:对于斜置于平面直角坐标系中的三角形,常将其进行“横切”或“竖切”(平行于坐标轴)分割成两个三角形,再进行面积计算.如图1,作 D E\perp x 轴交 B C 于点 E ,则 S_{\triangle B C D}=~S_{\triangle C D E}\;+ S_{\triangle B D E}=(1)/(2)D E* B O=(1)/(2)( y_{D}-y_{E} ) * \left( x_{B}-x_{C} \right).


2.割补法:将所求图形分割成以坐标轴为底的多个三角形或修补成矩形(边与坐标轴平行),然后利用图形面积公式进行和(差)计算即可.如图2,连接 \it{O D} ,则 S_{\triangle B C D}=\ S_{\scriptscriptstyle{v g i\underline{{{j}}}*\vec{\imath}* C D B O}}-S_{\triangle B O C}=\ S_{\triangle C D O}+ {\cal S}_{\triangle o D B}-{\cal S}_{\triangle B O C}.
3.平移法:一般过三角形某顶点作与另外两点构成线段的平行线,利用“平行线间的距离处处相等”,转化为求同底等高的三角形的面积.如图3,过点 D 作 Q D/B C 交 \boldsymbol{y} 轴于点 Q ,连接 B Q ,则 S_{\triangle B C D}=\DeltaS_{\triangle B C Q}
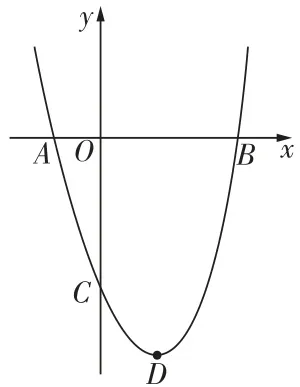
I题多解[2024 牡丹江中考]如图,二次函数y= y={(1)/(2)}x^{2}+b x+c 的图象与 x 轴交于 A ,B 两点,与 \boldsymbol{y} 轴交于点 C ,点 A 的坐标为(-1,0),点 C 的坐标为(0,-3),连接 B C
(1)求该二次函数的解析式;
(2)点 P 是抛物线在第四象限图象上的任意一点,当 \triangle B C P 的面积最大时,求点 P 的坐标;(3)在(2)的条件下, B C 边上的高 P N 的值为
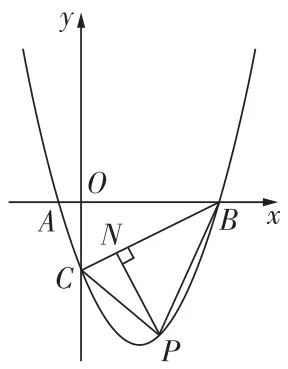
2如图,平面直角坐标系中,0 为坐标原点,抛物线=- y=\mathbf{α}-(1)/(2)x^{2}+b x+c 与 x 轴交于 A ,B 两点,与 \boldsymbol{y} 轴 的正半轴交于点 C ,且 B(4,0) B C=4√(2)
(1)求抛物线的解析式;
(2)P 是抛物线在第一象限内的一点,连接 P B,P C ,过点 P 作 P D\perp x 轴于点 D ,交 B C 于点 K. 记\triangle P B C,\triangle B D K 的面积分别为 S_{1} ,S_{2} ,求 S_{1}-S_{2} 的最大值.

3 如图,抛物线=- -x²+bx+c 与x轴交于A(4,0),B(-1,0)两点,与y轴交于点C,点D是抛物 线上一动点,点 E 是线段 A C 的中点,连接 A D ,以 A E 和 A D 为一组邻边作口ADGE.
(1)求抛物线的解析式;
(2)当点 D 在直线 A C 上方的抛物线上时,求 \square A D G E 面积的最大值及此时点 D 的坐标.
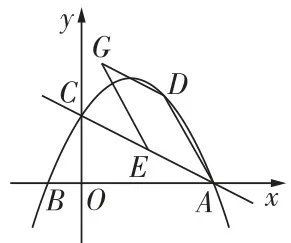
4[2024 泉州实验中学期中]已知直线 style y=2x+m 与抛物线 \ y=a x^{2}+a x+b 有一个公共点 M( 1 ,0 ) ,且 a<b
(1)求抛物线顶点 Q 的坐标(用含 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 的代数式表示);
(2)说明直线与抛物线有两个交点;
(3)若直线与抛物线的另一个交点记为 N ,求 \triangle Q M N 面积的最小值.
培优专项 二次函数中的存在性问题
过专项
阶段强化专项训练
答案 P6
1[2025福州延安中学期中]如图,抛物线 y=a x^{2}+b x+2 与 x 轴交于 A\left(\mathbf{\varepsilon}-1,0\right),B(4,0) 两点,与\boldsymbol{y} 轴交于点 C ,连接 B C ,顶点为 M.
(1)求抛物线的解析式及顶点 M 的坐标
(2)已知点 P 是抛物线上的一点,连接 C P ,是否存在点 P ,使得 \angle P C B=\angle A B C? 若存在,求出点 P 的坐标;若不存在,请说明理由.

2 0滚动·全等三角形[2025广州期中]如图,抛物线 \ y=x^{2} + b x + c 经过点(3,12)和(-2,-3),与两坐标轴的交点分别为 A,B,C ,它的对称轴为直线 l.
(1)求该抛物线的解析式
(2)P 是该抛物线上的点,过点 P 作 l 的垂线,垂足为点 D,E 是 l 上的点.是否存在以 P,D,E 为顶点的三角形与 \triangle A O C 全等?若存在,求满足条件的点 P 点 E 的坐标;若不存在,请说明理由.
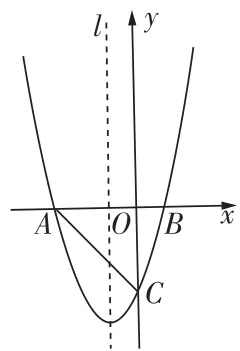
3 0滚动·直角三角形丨一题多解[2025义乌期中]如图,抛物线 \ y=x^{2} +b x +c 与 x 轴相交于 A ,B 两点,与 \boldsymbol{y} 轴相交于点 C ,对称轴为直线 x=2 ,顶点为 D ,点 B 的坐标为(3,0).
(1)求出点 A ,D 的坐标及抛物线的解析式
(2)P 是抛物线对称轴上一动点,是否存在点 P ,使 \triangle P A C 是以 A C 为斜边的直角三角形?若存在,请求出点 P 的坐标;若不存在,请说明理由.

4 滚动·平行四边形丨一题多解[2025 杭州外国语学校月考]如图,在平面直角坐标系中,二次函数²+ bx +c 的图象与x 轴相交于点 A(-2,0)和点 B(6,0),与 y轴交于点 C.
(1)求 b ,c 的值.
(2)点 F 是抛物线上的动点,作 E F//A C 交 x 轴于点 E ,是否存在点 F ,使得以 A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点 F 的坐标;若不存在,请说明理由.

数学活动
过基础 教材必备知识精练
答案P6
1[2025珠海期中]阅读材料:二次函数的应用
小明在学习过程中遇到一个问题:下列两个两位数相乘的运算中(两个乘数的十位上的数都是8,个位上的数的和等于10),猜想其中哪个积最大,并说明理由.
小明结合已学知识做了如下尝试:
设两个乘数的积为 \boldsymbol{y} ,其中一个乘数的个位上的数为 x ,则另一个乘数个位上的数为 \left( 10~-~x \right)
(1)问题解决:请帮助小明判断以上问题中哪个积最大,并求出这个最大的积;
(2)问题拓展:下列两个三位数相乘的运算中(两个乘数的百位上的数都是7,十位上的数与个位上的数组成的数的和等于100),用以上方法猜想其中哪个积最大,并说明理由.701x799 ,702x798 ,703x797 ,*s*s,797x703 ,798x702 ,799x701
2[2024 福州福清期中]如图,在平面直角坐标系中,点 A 的坐标是(0,2),在 x 轴上任取一点 M ,完成以下操作步骤:
① 连接 A M ,作线段AM的垂直平分线 l_{1} ,过点 M 作 x 轴的垂线 l_{2} ,记 l_{1},l_{2} 的交点为 P.
② 在 x 轴上多次改变点 M 的位置,用(1)的方法得到相应的点 P ,把这些点用平滑的曲线连接起来.观察画出的曲线 L ,猜想它是我们学过的哪种曲线
某数学兴趣小组在探究时发现在 x 轴上取几个特殊位置的点 M ,可以求出相对应的点 P 的坐标.
例如:取点 M(\mathit{\Pi}-4 ,0 ) ,过 P 作 P B\perp y 轴于点 B ,连接 A P_{
设 P(\ -4 ,y)
\therefore P M^{2}=y^{2}
在 Rt\triangle P A B 中,根据勾股定理得,
P A^{2}=P B^{2}+A B^{2}=
\because P 在 A M 的垂直平分线上,
\therefore\;P A=P M,
\therefore P M^{2}=P A^{2} ,
解得 y=
\therefore P(\mathit{\Pi}-4,5)
(1)请帮忙完成以上填空;

(2)请你帮该数学兴趣小组求出点 P 所在曲线 L 的解析式;
(3)兴趣小组在建立平面直角坐标系时受纸张大小的限制,若点 M 只能在 - 5<x<6 的范围内移动,求 \boldsymbol{y} 的取值范围.(直接写出答案)
章末复习专练
过易错
教材易混易错集训
答案P6
易错点1 忽略二次项系数的限制条件
1[2025泉州丰泽区月考]若 y=\left( m-2 \right)x^{ |m |} +1 是关于 x 的二次函数,则 m=
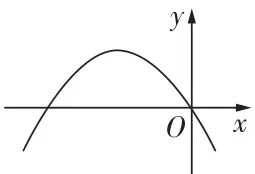
2[2025 龙岩初级中学月考]如图,二次函数 y=a x^{2} -3x +a^{2} -1 的图象经过原 点,那么 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 的值是
易错点2 忽略二次函数增减性的范围
3 已知二次函数 γ=3\left( x+2 \right)^{2} 的图象上有三点 A( 1 ,y_{1} ) ,B( 2 ,y_{2} )\;,C(\;- 3 ,y_{3} ) ,则 y_{1} ,y_{2} ,y_{3} 的大小关系为 )
A. y_{1}>y_{2}>y_{3} 3.\ y_{2}>y_{1}>y_{3} C.\ y_{3}>y_{1}>y_{2}\qquad\qquadD.\ y_{3}>y_{2}>y_{1}
[变式已知两点 \left( x_{1} ,y_{1} \right),\left( x_{2} ,y_{2} \right) 均在抛物线 \ y=x^{2} -1 上,给出下列说法: ① 若 \boldsymbol{y}_{1}=\boldsymbol{y}_{2} ,则 x_{1}=x_{2} :② 若 \dot{{x}}_{1} = - {x}_{2} ,则 \y_{1}=y_{2} : ③ 若 0<x_{1}<x_{2} ,则 \boldsymbol{y}_{1}>\boldsymbol{y}_{2} ④ 若 x_{1}<x_{2}<0 ,则 \boldsymbol{y}_{1}>\boldsymbol{y}_{2} .其中正确的说法是·(填序号)
4[2025 厦门华师希平双语学校月考]二次函数 y=x^{2}-2x+4 ,当自变量为 -1<=slant x<=slant2 时,函数值 \boldsymbol{y} 的最大值是
易错点3 错误使用抛物线的平移规律
5[2025福州一中月考]将抛物线 y= -2x^{2} 先向左平移4个单位长度,再向上平移5个单位长度,得到的抛物线的函数解析式为 (
A. y=- 2 {\left( x+4 \right)}^{ 2} -5 * γ= - 2\left( x+4 \right)^{2} +5\quad~C.~ y= - 2\left( x-4 \right)^{2} - 5\quad~D.~ y= - 2\left( x-4 \right)^{2} + 5
6[2025泉州实验中学月考]二次函数 y=-2x^{2}+8x+1 的图象如何平移可得到 y=-2x^{2} 的图象()
A.向左平移2个单位长度,向上平移9个单位长度B.向右平移2个单位长度,向上平移9个单位长度C.向左平移2个单位长度,向下平移9个单位长度D.向右平移2个单位长度,向下平移9个单位长度
7若二次函数 \ y=a x^{2}+b x+c 的图象先向右平移3个单位长度,再向下平移2个单位长度,所得图象的解析式是 y=x^{2}-4x+5 ,则 a+b+c=
易错点4 忽视隐含条件
8[2025北京期中]关于 x 的函数 γ=k x^{2}-2x+1 的图象与 x 轴有两个交点,则 k 的取值范围是(
A. k<1 且 k\neq0 B. k<1 {C}.\;k<=slant1\qquad\qquad\qquad{D}.\;k\neq0
9已知抛物线y=-x x²+(6-√m)x+m-3与x轴交于A,B两点,且点A,B关于y轴对称,求此抛物线的解析式.
过全章 题串练透全章知识
已知抛物线 \ y=x^{2}+b x+c 经过原点,且对称轴为直线 x=1
【基础设问】
(1)求该抛物线的解析式
(2)在如图所示的平面直角坐标系中画出该抛物线(3)根据图象,回答下列问题:① 开口方向是 ,顶点坐标为② 当 x 时, \boldsymbol{y} 随 x 的增大而增大;③ 一元二次方程 x^{2}+b x+c=0 的解为④ 不等式 x^{2}+b x+c>0 的解集为⑤ 当 0<=slantx<=slant3 时, \boldsymbol{y} 的取值范围为⑥ 若直线 γ=3 与抛物线 \ y=x^{2}+b x+c 交于 M,N 两点,若点 M,N 的横坐标分别为 m ,n ,则 m+n=
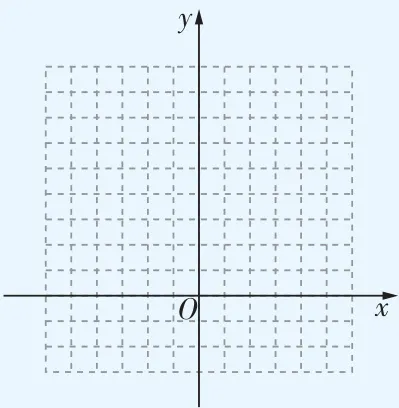
【能力设问】
(4)将抛物线 \ y=x^{2}+b x+c 向右平移1个单位长度,得到抛物线 G. 已知抛物线 G 与 x 轴交于 A ,B 两点(点 A 在点 B 左侧),与 \boldsymbol{y} 轴交于点 C ① 求抛物线 G 的解析式;② 若点 D 是抛物线 G 对称轴上的一动点,当 D A+D C 最小时,点 D 的坐标;③ 若点 E 是抛物线 G 上的一点,且点 E 在直线 B C 的下方,求 S_{\triangle B C E} 的最大值;④ 垂直于 \boldsymbol{y} 轴的直线 l 与抛物线 G 交于 P(it{x}_{1},it{y}_{1}) ,Q(it{x}_{2},γ_{2}) 两点,与直线 B C 交于点 H(\mathbf{\nabla}\ x_{3} ,γ_{3} ),若 x_{1}<x_{2}<x_{3} ,求 x_{1}+x_{2}+x_{3} 的取值范围.
【拓展设问】
(5)某公司销售一种新型节能电子小产品,现准备从国内和国外两种销售方案中选择一种进行销售: ① 若只在国内销售,销售价格 \boldsymbol{y} (元/件)与月销量 x (件)的函数关系式为 y= - {(1)/(100)}x +150 成本为20元/件,月利润为 {\mathbb{W}}_{1} 元; ② 若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 元/件( \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 为常数, 10<=slanta<=slant40\;. ),当月销量为 x 件 ( x>2 ) 时,每月还需缴纳 {(1)/(100)}( x^{2} + b x+c) 元的附加费,月利润为 W_{2} 元.若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 的值.
章末滚动:过全章,通过一题多设问的方式将全章内容进行串联和深度融合,由点到面整合教材内容
过中考
考点1:二次函数的图象与性质 T2,T4,T5 考点2:二次函数图象的平移T3
考点3:与系数 a,b ,c 有关的判断 T1 考点4:二次函数的实际应用T6
1[2024 湖北中考]已知抛物线 y=a x^{2} +b x +c ( a ,b ,c 为常数, a\neq0 )的顶点坐标为(-1,-2),与\boldsymbol{y} 轴的交点在 x 轴上方.下列结论正确的是 (
A. a<0 ~B~{\it c}<0 C.\;a-b+c=- 2\;\;\;\;\;\;\;\;\;\;\;\;D.\;b^{2}-4a c=0
2 新考法[2024 福建中考]已知二次函数 y=x^{2} -2a x +a\bigl( a\neq0 \bigr) 的图象经过 A\big((a)/(2),y_{1}\big) , B( 3a ,y_{2} ) 两点,则下列判断正确的是 ()
A.可以找到一个实数 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} ,使得 γ_{1}>a B.无论实数 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 取什么值,都有 γ_{1}>a C.可以找到一个实数 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} ,使得 y_{2}<0 D.无论实数 \footnote{A l l t h e p a r a m e t e r s a r e e m p i r i c a l l y d e t e r m i n e d u s i n g t h e g e n e r a l w o r k f l o w,w h e r e t h e t r a i n i n g s t a r t s w i t h r e l a t i v e l y s m a l l v a l u e s a n d i n c r e a s e s t h e v a l u e s u n t i l t h e l e a r n i n g p e r f o r m a n c e c a n n o t b e f u r t h e r i m p r o v e d.} 取什么值,都有 γ_{2}<0
3[2024 牡丹江中考]将抛物线 \ y=a x^{2}+b x+3 向下平移5个单位长度后,经过点(-2,4),则 6a~-~ 3b-7=
4[2023 福建中考]已知抛物线 y=a x^{2}-2a x+b( a>0 ) 经过 A\big(2n+3 ,y_{1}\big) ,B\big( n-1 ,y_{2} \big) 两点,若 A ,B 分别位于抛物线对称轴的两侧,且 y_{1}<y_{2} ,则 n 的取值范围是
5[2024福建中考]如图,已知二次函数 \ y=x^{2} + b x + c 的图象与 x 轴交于 A ,B 两点,与 \boldsymbol{y} 轴交于点C ,其中 \boldsymbol{A}(\ -2 ,0) ,\boldsymbol{C}(0 , -2 )
(1)求二次函数的解析式;
(2)若 P 是二次函数图象上的一点,且点 P 在第二象限,线段 P C 交 x 轴于点D ),\triangle P D B 的面积是 \triangle C D B 的面积的2倍,求点 P 的坐标.

6[2024 河南中考]从地面竖直向上发射的物体离地面的高度 h(\mathbf{δm}) 满足关系式 h= -5t^{2}+v_{0}t ,其中t\left(rm{s}\right) 是物体运动的时间, v_{0} ( m/s ) 是物体被发射时的速度.社团活动时,科学小组在实验楼前从地面竖直向上发射小球.
(1)小球被发射后 s 时离地面的高度最大(用含 v_{0} 的式子表示).
(2)若小球离地面的最大高度为 20rm{m} ,求小球被发射时的速度.
(3)按(2)中的速度发射小球,小球离地面的高度有两次与实验楼的高度相同.小明说:“这两次间隔的时间为3s.”已知实验楼高 15 ~m~ ,请判断他的说法是否正确,并说明理由.
答案 P30
综合与实践
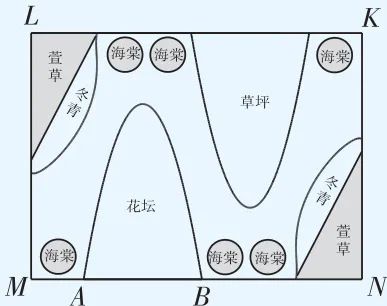
[2024 山西中考]问题情境:如图1,矩形 MNKL 是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段 A B 组成的封闭图形,点 A ,B 在矩形的边MN上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校面向全体同学征集设计方案.
方案设计:如图2, A B=6 米, A B 的垂直平分线与抛物线交于点 P ,与 A B 交于点 o ,点 P 是抛物线的顶点,且 P O=9 米.欣欣设计的方案如下:
第一步:在线段 O P 上确定点 C ,使 \angle A C B=90°. 用篱笆沿线段 A C,B C 分隔出 \triangle A B C 区域,种植串串红;
第二步:在线段 {C P} 上取点 F (不与 {\cal C} ,P 重合),过点 F 作 A B 的平行线,交抛物线于点 D,E. 用篱笆沿 D E,C F 将线段 A C,B C 与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.
方案实施:学校采用了欣欣的方案,在完成第一步 \triangle A B C 区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定 D E 与 C F 的长.为此,欣欣在图2 中以 A B 所在直线为 x 轴, O P 所在直线为 \boldsymbol{y} 轴建立平面直角坐标系.请按照她的方法解决问题:
(2)求6 米材料恰好用完时 D E 与 C F 的长.
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段A C,B C 上.直接写出符合设计要求的矩形周长的最大值.

福建中考题型
综合与实践,创设真实情境,提高问题解决能力

同步学习王炸组合

课前预习《教材帮》课后练习《一遍过》




































 该页无缩略图
该页无缩略图



