复合材料科学与工程
3? 2 纤维缠绕层模型
对于复合材料层ꎬ其螺旋层及环向层的总厚度
t
fα和 t
fβ采用网格理论[12]进行确定:
t
fα
=
R?Pb
2?k?σfb?cos
2
α
t
fβ
=
R?Pb
2?σfb
2 - tan
2
( α)
ì
î
í
ï
ï
ï
ï
ïï
(1)
式中:R 为铝合金内衬筒身段半径ꎻPb 为压力容器
的最小设计爆压ꎻσfb为纤维的许用强度ꎻk 为螺旋缠
绕的应力平衡系数ꎬ其取值范围为 0? 65 ~ 0? 85ꎻα 为
筒身段螺旋缠绕角度ꎮ
本文中纤维缠绕压力容器的工作压力为 35 MPaꎬ
其设计依据为 GB / T 35544—2017«车用压缩氢铝内
衬碳纤维全缠绕气瓶»ꎮ 水压试验压力为 52? 5 MPaꎬ
最小设计爆破压力为 78? 75 MPaꎮ 纤维单层厚度为
0? 2 mmꎬ纤维许用强度为 1950 MPaꎬ计算所得缠绕
铺层方案为:[±112
/ 906
/ ±112
/ 906
/ ±11 / 902 ]ꎮ
对于纤维缠绕层的建模ꎬ为了描述纤维缠绕压
力容器在封头段的变角度变厚度特性ꎬ使用 Python
脚本结合三次样条厚度预测公式ꎬ对封头段厚度进
行建模ꎬ封头段两个带宽内的厚度计算方法如下:
t(r)=m1
× r
0 + m2
× r
1 + m3
× r
2 + m4
× r
3
(2)
其中系数 m1 、m2 、m3 和 m4 求解方法如下:
m1
m2
m3
m4
é
ë
ê
ê
ê
ê
ê
ê
ù
û
ú
ú
ú
ú
ú
ú
=
1 r0
r
2
0
r
3
0
1 r2b
r
2
2b
r
3
2b
0 1 2r2b 3r
2
2b
π(r
2
2b
-r
2
0 )
2π
3
(r
3
2b
-r
3
0 )
π
2
(r
4
2b
-r
4
0 )
2π
5
(r
5
2b
-r
5
0 )
é
ë
ê
ê
ê
ê
ê
ê
êê
ù
û
ú
ú
ú
ú
ú
ú
úú
-1
×
tR?πR?cosα0
/ (m0?b)
mR?nR
π
arccos
r0
r2b
æ
è
ç
ö
ø
÷ - arccos
r0
+ b
r2b
æ
è
ç
ö
ø
÷
é
ë
ê
ê
ù
û
ú
ú?tR?M
mR?nR
π
r0
r2b
r
2
2b
- r
2
0
-
rb
r2b
r
2
2b
- r
2
b
æ
è
çç
ö
ø
÷÷?tR?M
Vconst
ì
î
í
ï
ï
ï
ï
ï
ï
ï
ï
ïï
ü
þ
ý
ï
ï
ï
ï
ï
ï
ï
ï
ïï
(3)
式中ꎬVconst为两个带宽处的纤维体积ꎬ其计算方法
如下:
M =1 / arcsin
(R
2 - r
2
0 ) - (R
2 - r
2
b) + b
2 [ ]
2R { }
(4)
Vconst
=∫
rb
r0
2πr?
mR?nR
π
?arccos
r0
r
æ
è
ç
ö
ø
÷?t
p dr +∫
r2b
rb
2πr?
mR?nR
π
? arccos
r0
r2b
æ
è
ç
ö
ø
÷ - arccos
r0
+ b
r2b
æ
è
ç
ö
ø
÷
é
ë
ê
ê
ù
û
ú
ú?tR?Mdr
(5)
其中:ri 为缠绕位置的平行圆半径ꎻr0 为极孔半径ꎻrb
为一个带宽处的平行圆半径ꎻr2b为两个带宽处的平
行圆半径ꎻtR 为缠绕层在筒身段的厚度ꎻnR 为筒身
段螺旋缠绕单层数ꎻmR 为筒身段纱片数ꎻn0 为极孔
处的缠绕单层数ꎻm0 为极孔处的纱片数ꎮ
在两个带宽外区域的纤维厚度计算方法为:
t(r)=
mR?nR
π
arccos
r0
r2b
- arccos
(r0
+ b)
r2b
é
ë
ê
ê
ù
û
ú
ú?tR?M
(6)
通过 Python 脚本可以将纤维缠绕层的每一层
厚度分布描绘出来ꎬ下一层纤维的厚度分布则通过
上一层纤维的外轮廓确定ꎮ 所得纤维层厚度分布如
图 6 所示ꎮ
图 6 纤维缠绕层厚度及角度分布示意图
Fig? 6 Schematic diagram of thickness and
angle distribution of filament wound layer
碳纤维缠绕层在封头处的角度分布通过测地线
缠绕公式来确定:
α(r)=arcsin(r0
/ r) (7)
2021 年第 12 期 43
???????????????????????????????????????????????
基于精细化模型的纤维缠绕压力容器失效行为及容积特性影响因素分析
3? 3 有限元计算模型
对于轴对称模型ꎬ为提高计算效率及精度ꎬ一般
不采用全模型进行计算ꎬ本文采用 1 / 2 模型进行后
续的有限元计算分析ꎬ最终用于有限元计算模型如
图 7 所示ꎮ
图 7 压力容器计算模型
Fig? 7 Pressure vessel calculation model
由于纤维缠绕层模型是逐层建立的ꎬ可以在层间
插入黏性层ꎬ用以表征缠绕层间的分层损伤情况ꎮ 铝
合金内衬及纤维缠绕层均采用 C3D8R 单元(八结点
线性六面体单元ꎬ采用减缩积分及沙漏控制)ꎬ部分
网格过渡区域采用 C3D6 单元(六节点单元)ꎬ其中
黏性单元采用 COH3D8 单元(八结点三维黏结单元)ꎮ
3? 4 材料属性
纤维缠绕压力容器内衬材料为 6061 ̄T6 铝合
金ꎬ增强纤维材料为 T700CS ̄12K 碳纤维ꎬ树脂材料
为 EW ̄60D 环氧树脂ꎬ采用湿法缠绕后固化成型工
艺ꎮ 其材料性能如表 1、表 2 所示ꎮ 内聚力单元材
料属性如表 3 所示ꎮ
表 1 铝合金材料力学性能参数
Table 1 Mechanical properties of aluminum alloy
参 数 数 值
弹性模量 E/ GPa 74.1
泊松比 μ 0.28
屈服强度/ MPa 281
屈服极限/ MPa 340
密度/ kg?m
-3 2800
表 2 T700 碳纤维/ 环氧树脂力学性能参数
Table 2 Mechanical properties of T700 carbon fiber/epoxy resin
参 数 数 值
纵向拉伸模量 E1
/ GPa 134
横向拉伸模量 E2
=E3
/ GPa 7.42
面内泊松比 μ12
= μ13 0.28
面外泊松比 μ23 0.3
面内剪切模量 G12
=G13
/ GPa 3.71
层间剪切模量 G23
/ GPa 4.79
纵向拉伸强度 Xt
/ MPa 1950
纵向压缩强度 Xc
/ MPa 1250
横向拉伸强度 Yt
/ MPa 74
横向压缩强度 Yc
/ MPa 180
面内剪切强度 S / MPa 50
密度 ρ / kg?m
-3 1680
表 3 黏性层力学性能参数
Table 3 Interfacial cohesive properties
界面参数 数 值
弹性模量 E/ GPa 3.0
泊松比 μ 0.35
拉伸强度 Sn
/ MPa 30
剪切强度 Ss
= St
/ MPa 45
拉伸断裂韧性 Gnc
/ N?mm
-1
0.28
剪切断裂韧性 Gsc
/ N?mm
-1
0.79
3? 5 边界条件
纤维缠绕压力容器爆破压强计算模型的边界条
件主要包括图 8(a)所示循环对称边界条件、图 8(b)
所示侧剖面在柱坐标系(RTZ)下的环向对称约束、
图 8(c)所示下端面的固定约束及图 8(d)所示铝合
金内衬内表面的压强载荷ꎮ 具体约束的施加如图 8
所示ꎮ
图 8 边界条件施加示意图
Fig? 8 Schematic diagram of boundary condition imposition
44 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
3? 6 渐进损伤计算方法
渐进损伤计算方法通过 Hashin 失效准则判断
纤维和基体的失效情况ꎬ结合 Quads 准则对层间黏
性单元层进行失效判断ꎮ 计算过程包括应力计算、
失效判断和材料退化三个部分ꎮ 通过应力计算结合
Hashin 失效判据对各单元的损伤情况进行判断ꎬ若
出现损伤则对相应单元的材料进行刚度折减ꎬ其刚
度折减规则参照 Camonho 材料退化模型[13]
ꎬ具体退
化准则如表 4 所示ꎬ当整个模型的刚度折减累积到
一定程度时整个结构出现结构失效ꎮ 通过结构失效
对应的载荷来判断爆破压强的大小ꎮ 渐进损伤计算
流程图如图 9 所示ꎮ
表 4 材料性能退化准则
Table 4 Criteria for material degradation
失效模式 退化准则
基体开裂 E22
= 0.2E22 ꎬ G12
= 0.2G12 ꎬ G23
= 0.2G23
基体挤裂 E22
= 0.4E22 ꎬ G12
= 0.4G12 ꎬ G23
= 0.4G23
纤维拉伸
破坏
E11
= 0.07E11 ꎬ E22
= 0.07E22 ꎬ E33
= 0.07E33 ꎬ G12
= 0.07G12
G13
= 0.07G13 ꎬ v12
= 0.07v12 ꎬ v13
= 0.07v13 ꎬ v23
= 0.07v23
纤维压缩
破坏
E11
= 0.14E11 ꎬ E22
= 0.14E22 ꎬ E33
= 0.14E33 ꎬ G12
= 0.14G12
G13
= 0.14G13 ꎬ v12
= 0.14v12 ꎬ v13
= 0.14v13 ꎬ v23
= 0.14v23
图 9 渐进损伤计算流程图
Fig? 9 Computational flow chart
Hashin 失效准则包括纤维的拉伸与剪切破坏、
纤维的压缩与剪切破坏、基体拉伸与剪切破坏以及
基体压缩与剪切破坏四种ꎬ在 Abaqus 中以结果状态
定义变量来表示ꎬ具体计算方式如下:
纤维拉伸及剪切破坏(σ11≥0):
σ1
Xt
æ
è
ç
ö
ø
÷
2
+ α
τ12
S12
æ
è
ç
ö
ø
÷ +
τ13
S13
æ
è
ç
ö
ø
÷
é
ë
ê
ê
ù
û
ú
ú
2
≥1 (8)
纤维压缩及剪切破坏(σ11<0):
σ1
Xc
æ
è
ç
ö
ø
÷
2
≥1 (9)
基体拉伸及剪切破坏(σ22
+σ33≥0):
σ2
+σ3
Yt
æ
è
ç
ö
ø
÷
2
+
τ
2
12
+ τ
2
13
S
2
12
+
τ
2
23
-σ2?σ3
S
2
23
≥1 (10)
基体压缩及剪切破坏(σ22
+σ33<0):
Yc
2S23
æ
è
ç
ö
ø
÷
2
- 1
é
ë
ê
ê
ù
û
ú
ú?
σ2
+σ3
Yc
+
σ2
+σ3
2S23
æ
è
ç
ö
ø
÷
2
+
τ
2
12
+ τ
2
13
S
2
12
+
τ
2
23
-σ2?σ3
S
2
23
≥1
(11)
4 结果与讨论
4? 1 纤维缠绕压力容器有限元结果分析
通过渐进损伤计算结果可以看出纤维缠绕压力
容器出现结构失效的主要原因是筒身段环向层纤维
发生大面积拉伸断裂损伤[14 ̄16]
ꎮ 且压力容器发生结
构失效时ꎬ螺旋缠绕层出现了大面积基体拉伸损伤ꎬ
纤维缠绕层间也出现了较大面积的分层现象ꎮ 图
10 给出了压力容器发生结构失效时各损伤结果ꎬ为
了使结果呈现得更加直观ꎬ将纤维拉伸损伤结果中
最内层的螺旋层在结果显示时去除一半ꎬ从实际损
伤结果可以看出ꎬ导致内胆出现爆破的主要原因是
筒身段环向缠绕纤维出现大面积损伤ꎬ与纤维拉伸
损伤结果一致ꎻ与此同时ꎬ各纤维缠绕层间及纤维层
与铝合金内衬脱开ꎬ与层间损伤计算结果[17 ̄20]一致ꎮ
图 10 结构发生失效时压力容器损伤结果
Fig? 10 The damage result when structure failed
最终爆破压力值通过筒身段的载荷 ̄径向位移曲
线来确定ꎬ通过渐进损伤计算出的精确爆压为曲线
发生位移突变的点ꎬ即本文所设计的压力容器计算
爆压为 73? 5 MPaꎬ与实际打爆结果误差为 3? 3%ꎮ 载
荷位移曲线如图 11 所示ꎬ图中也将实际测量值与计
算值进行了对比ꎮ 图 12 为测点 2 和测点 5 应变实
2021 年第 12 期 45
???????????????????????????????????????????????
基于精细化模型的纤维缠绕压力容器失效行为及容积特性影响因素分析
际测量结果与计算值的对比ꎬ由于实际应变片手动
铺贴与预设值有偏差ꎬ最终误差在 10%以内ꎮ
图 11 载荷 ̄径向位移曲线
Fig? 11 Load ̄radial displacement curve
图 12 载荷 ̄应变曲线
Fig? 12 Load ̄strain curve
4? 2 压力容器容积特性分析
本文对不同容积与不同设计爆压的压力容器进
行了容积特性分析(容积特性系数可以用来评价压
力容器的承载性能ꎬ其值越高代表压力容器的承载
性能越优异)ꎮ 研究对象为试验常用的 6? 8 L、9 L
及 18 L 压力容器ꎬ在筒身段长径比(本文中用以表
示容器筒身长度和筒身直径的比值)、封头段椭球比
及极孔半径与筒身段半径比值(下文中简称为开口
比)、设计方法及参数一致的前提下ꎬ分别计算了各
型号压力容器在设计爆压为 20 MPa~120 MPa 的容
积特性系数 PV / Wꎻ为了更加精确地描述碳纤维缠
绕层的承载性能ꎬ同时计算了纤维层容积特性系数
PcV/ Wcꎬ其中 Pc 为压力容器总体爆压与铝合金内衬
爆压之差ꎬV 为压力容器容积ꎬWc 为纤维缠绕层重
量ꎮ 其计算结果如图 13 所示ꎬ从计算结果可以看出:
①容积特性 PV/ W 随着容积的增加而增大ꎬ并随着设
计爆压的增加而增大ꎻ②容积特性 PcV / Wc 随着容积
的增加而增大ꎬ并随着设计爆压的增加而略微减小ꎮ
(a)6.8 L
(b)9.0 L
(c)18 L
图 13 不同型号压力容器容积特性变化曲线
Fig? 13 Volume characteristic curve of pressure
vessels of different types
在此基础上研究了长径比(筒身段长度与筒身
段直径的比值) 对容积特性系数 PcV / Wc 的影响ꎮ
在气瓶内胆容积、椭球比、开口比及设计方法、参数
一致的前提下ꎬ计算了容积为 9 L、椭球比为 2 、开
口比为 0? 19 的压力容器不同长径比对容积特性的
影响ꎮ 计算的 5 组压力容器的尺寸参数如表 5 所
示ꎬ其容积特性系数 PcV / Wc 变化曲线如图 14 所示ꎮ
46 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
表 5 内衬尺寸参数
Table 5 Dimension parameters of lining
参 数
数 值
1 2 3 4 5
长径比 i 1.5 2 2.5 3 3.5
筒身段直径/ mm 179.8 166.8 156.8 148.8 142.4
短半轴长/ mm 63.5 59.0 55.4 52.6 50.3
筒身段长/ mm 269.7 333.5 392.0 446.7 498.3
图 14 容积特性随长径比变化曲线
Fig? 14 Volume characteristic curve with aspect ratio
从计算结果可以看出ꎬ容积特性系数 PcV/ Wc 随
着长径比的增大而减小ꎮ
5 结 论
本文通过对纤维缠绕压力容器的三维扫描实验
对比厚度预测公式ꎬ给出了一种高精度的有限元建
模方法ꎮ 基于该方法进行了小型压力容器的设计计
算ꎬ并通过水压爆破实验进行验证ꎮ 结果表明:
(1)三次样条厚度预测方法能准确预测测地线
纤维缠绕层在封头处的厚度分布情况ꎮ
(2)采用缠绕层逐层建立并在层间插入黏性层
单元结合 Hashin 失效判据的渐进损伤计算方法ꎬ能够
精准、全面以及直观地判断压力容器的各种损伤情况ꎮ
(3)压力容器水压试验结果为 76 MPaꎬ与有限
元计算结果误差为 3? 3%ꎮ 位移应变结果与实际测
量值误差在 10%以内ꎬ表明通过载荷位移曲线破坏
位置的位移突变确定爆破压强是合理的ꎮ
(4)对于Ⅲ型压力容器ꎬ可以通过增大设计爆
压提高容器的容积特性系数ꎻ且相同容积压力容器
的容积特性随着长径比的增加而减小ꎮ
参考文献
[1] REN M Fꎬ CHANG Xꎬ XU H Yꎬ et al. Trans ̄scale analysis of com ̄
posite overwrapped pressure vessel at cryogenic temperature[J]. Com ̄
posite Structuresꎬ 2016ꎬ 160: 1339 ̄1347.
[2] 杨文刚ꎬ 李文斌ꎬ 林松ꎬ 等. 碳纤维缠绕复合材料储氢气瓶的研
制与应用进展[J]. 玻璃钢/ 复合材料ꎬ 2015(12): 99 ̄104.
[3] ZU Lꎬ XU Hꎬ WANG H Bꎬ et al. Design and analysis of filament
wound composite pressure vessels based on non ̄geodesic winding[J].
Composite Structuresꎬ 2019ꎬ 207: 41 ̄52.
[4] ZHANG Qꎬ XU Hꎬ JIA X L. Design of a 70 MPa type Ⅳ hydrogen
storage vessel using accurate modeling techniques for dome thickness
prediction[J]. Composite Structuresꎬ 2020ꎬ 236: 111915.
[5] 王华毕ꎬ 程硕ꎬ 祖磊ꎬ 等. 复合材料储氢气瓶的纤维厚度预测与
强度分析[J]. 复合材料科学与工程ꎬ 2020(5): 5 ̄11.
[6] 王亮. 基于微观力学分析的复合材料储氢容器强度与寿命研究
[D]. 杭州: 浙江大学ꎬ 2016.
[7] NEBE Mꎬ SORIANO A. Analysis on the mechanical response of com ̄
posite pressure vessels during internal pressure loading: FE modeling
and experimental correlation[ J]. Composites Part B: Engineeringꎬ
2021ꎬ 212: 1359 ̄8368.
[8] LIU P Fꎬ CHU J Kꎬ HOU S Jꎬ et al. Micromechanical damage mod ̄
eling and multiscale progressive failure analysis of composite pressure
vessel[J]. Computational Materials Scienceꎬ 2012ꎬ 60: 137 ̄148.
[ 9] RAMIREZ J P Bꎬ HALM Dꎬ GRANDIDIER J Cꎬ et al. 700 bar type
Ⅳ high pressure hydrogen storage vessel burst simulation and exper ̄
mental validation[ J]. International Journal of Energyꎬ 2015ꎬ 40:
13183 ̄13192.
[10] 矫维成ꎬ 王荣国ꎬ 刘文博ꎬ 等. 纤维缠绕复合材料压力容器封
头厚度预测[J]. 复合材料学报ꎬ 2010ꎬ 27(5): 116 ̄121.
[11] HASHIN Z. Failure criteria for unidirectional fiber compositer[ J].
Journal of Applied Mechanicsꎬ 1980ꎬ 47(2): 329 ̄334.
[12] 陈汝训. 纤维缠绕壳体设计的网格分析方法[ J]. 固体火箭技
术ꎬ 2003ꎬ 26(1): 30 ̄32.
[13] Lessard L B. Comparison failure in laminated composites containing
an open hole[D]. Stanfordꎬ USA: Stanford Universityꎬ 1991.
[14] WANG Qꎬ LI TONGꎬ WANG BOꎬ et al. Prediction of void growth
and fiber volume fraction based on filament winding process me ̄
chanics[J]. Composite Structuresꎬ 2020ꎬ 246: 112432.
[15] CAMANHO P Pꎬ MATTHEWS F L. A progressvie damage model
for mechanically fastened joints in composite laminates[J]. Journal
of Composite Materialsꎬ 1999ꎬ 33(24): 2248 ̄2280.
[16] 杨帆. 冲击作用下复合材料气瓶损伤形态与剩余强度[D]. 大
连: 大连理工大学ꎬ 2019.
[17] LIU P Fꎬ CHU J Kꎬ et al. Micromechanical damage modeling and
multiscale progressive failure analysis of composite pressure vessel
[J]. Computational Materials Scienceꎬ 2012ꎬ 60: 137 ̄148.
[18] 王晓宏ꎬ 张博明ꎬ 刘长喜ꎬ 等. 纤维缠绕复合材料压力容器渐
进损伤分析[J]. 计算力学学报ꎬ 2009ꎬ 26(3): 446 ̄452.
[19] 安文奇ꎬ 路智敏ꎬ 赵飞ꎬ 等. 金属内衬碳纤维复合材料压力容器
壳体的有限元分析[J]. 内蒙古工业大学学报(自然科学版)ꎬ
2017ꎬ 36(4): 18 ̄23.
[20] RAFIEE Rꎬ TORABI M A. Stochastic prediction of burst pressure
in composite pressure vessels [ J]. Composite Structuresꎬ 2017ꎬ
185: 573 ̄583.
2021 年第 12 期 47
???????????????????????????????????????????????
基于分布式光纤传感技术的 CFRP 板变形监测研究
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 007
基于分布式光纤传感技术的 CFRP 板变形监测研究
何建平1
ꎬ 沈 锋2
ꎬ 张世海3
(1? 大连理工大学 土木工程学院ꎬ 大连 116024ꎻ 2? 江苏飞博尔新材料科技有限公司ꎬ 盐城 224700ꎻ
3? 南阳理工学院 土木工程学院ꎬ 南阳 473001)
摘要: 碳纤维增强复合材料(CFRP)具有优良的抗拉强度和耐腐蚀性ꎬ被广泛应用于支护和加固结构中ꎮ 为研究碳纤维
复合材料使用过程中的变形特性ꎬ在 CFRP 板上布设分布式光纤传感器ꎬ开展 CFRP 板有损和无损两个工况下的变形监测试
验ꎬ并在 CFRP 板上布设电阻应变片进行应变测试对比ꎮ 试验结果表明:分布式光纤传感器能够有效测量 CFRP 板各处的应变
信息ꎬ测量应变与有限元分析值、电阻应变片测量值基本吻合ꎬ分布式光纤传感器连续布设比定点布设更能真实反映 CFRP 板
变形ꎮ
关键词: CFRPꎻ 分布式光纤传感器ꎻ 应变ꎻ 损伤监测
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0048-05
Research on deformation monitoring of CFRP plate using distributed optical fiber sensing technology
HE Jian ̄ping
1
ꎬ SHEN Feng
2
ꎬ ZHANG Shi ̄hai
3
(1? School of Civil Engineeringꎬ Dalian University of Technologyꎬ Dalian 116024ꎬ Chinaꎻ
2? Jiangsu Fiber Composite Co.ꎬ Ltd.ꎬ Yancheng 224700ꎬ Chinaꎻ
3? School of Civil Engineeringꎬ Nanyang Institute of Technologyꎬ Nanyang 473001ꎬ China)
Abstract:Carbon fiber reinforced polymer ( CFRP) has been widely used in supporting and strengthening
structures due to its excellent tensile strength and corrosion resistance. In order to study the deformation characteris ̄
tics of CFRP in serviceꎬ distributed optical fiber sensors were placed on the CFRP plate to carry out deformation
monitoring tests of CFRP plate under two working conditions of damage and non damageꎬ and resistance strain gau ̄
ges were placed on the CFRP plate for strain test comparison. The experimental results show that the distributed op ̄
tical fiber sensor can effectively measure the strain information of the CFRP plateꎬ and the measured strain is basi ̄
cally consistent with the finite element analysis value and the resistance strain gauge value. The continuous arrange ̄
ment of the distributed optical fiber sensor is more realistic than the fixed ̄point arrangement to reflect the deforma ̄
tion of the CFRP plate.
Key words:CFRPꎻ distributed optical fiber sensorꎻ strainꎻ damage monitoring
收稿日期: 2021 ̄03 ̄29
基金项目: 国家自然科学基金项目 (61875027ꎬ 61675102)ꎻ 中央高校基本科研业务费项目 (DUT20LAB140)
作者简介: 何建平 (1976 ̄)ꎬ 男ꎬ 博士/ 博士后ꎬ 副教授ꎬ 主要从事光纤传感、 纤维复合智能结构及结构监测与评定方面的研究ꎬ
hejianp@dlut? edu? cnꎮ
诸如碳纤维、玻璃纤维、玄武岩纤维等纤维增强
聚合物(FRP)复合材料具有重量轻、强度高、耐腐蚀
性强等特点ꎬ目前已经在航空航天、航海、土木工程、
港口等结构或基础设施中得到了越来越广泛的应
用ꎮ 譬如我国国产大飞机 C919 大量采用复合材料ꎬ
用量达到 12%ꎻ在海港工程结构中ꎬFRP 筋有取代
传统受力钢筋的趋势ꎮ FRP 材料虽然具有良好的力
学和耐久性能ꎬ但是在高应力、紫外线等联合作用下
不可避免地会发生损伤ꎬ导致其承载能力下降ꎮ 譬如ꎬ
因环氧树脂胶粘贴工艺不达标ꎬ导致桥梁 CFRP 板
加固能力下降[1]
ꎻ因环境腐蚀ꎬFRP 筋与结构黏结
性能下降ꎬ导致结构承载能力下降[2]
ꎻ且 FRP 材料
自身在疲劳载荷作用下ꎬ其剩余刚度或使用寿命也
会逐渐降低[3]
ꎮ FRP 材料损伤或承载能力下降ꎬ会
影响结构的服役安全和使用寿命ꎬ因此有必要对
FRP 结构的力学性能进行监测[4]
ꎮ 蔚道祥等采用声
48 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
发射技术对 FRP 复合材料容器的损伤检测进行了研
究ꎬ实现了 FRP 材料的衰减测量和定位[5]
ꎮ 李伟等
运用三维参数法ꎬ分析研究了 FRP 材料声发射信号
的特征规律并从宏观上描述了 FRP 材料拉伸破坏规
律[6]
ꎮ Schulte 等采用电阻法对纤维增强复合材料
的拉伸损伤进行检测研究[7]
ꎮ 光纤的主要成分是二
氧化硅ꎬ热膨胀系数与纤维(特别是玻璃纤维)比较
相近ꎬ此外光纤本身体积小且抗电磁场干扰ꎬ被广泛
应用于航空工业和复合材料受力构件的监测中ꎮ 蒋
园园将光纤光栅传感器埋入热压罐成型的碳纤维材
料中ꎬ开展罐的损伤监测ꎬ解决了光纤引出保护的问
题[8]
ꎮ 吴慧峰基于光纤光栅传感技术开展飞机机翼
动态和静态两个工况下的形变测量ꎬ通过应变 ̄挠度
曲线关系重构机翼的形态[9]
ꎮ 李小伟基于光纤光栅
传感技术开展风机叶片检测ꎬ研究了光纤光栅传感
器在风机叶片中的布设位置与损伤信号的关系[10]
ꎮ
何建平等将光纤或光纤光栅植入 FRP 中研发 FRP 智
能筋ꎬ并将其应用到高速铁路路基沉降监测中ꎬ测试
效果证明光纤与 FRP 材料具有很好的协同变形且
FRP 能够有效保护传感光纤[11ꎬ12]
ꎮ Wang 等研究了
CFRP ̄FBG 复合材料加固钢结构的界面粘贴状态[13]
ꎬ
并对 FBG 植入纤维增强复合材料中的应变传递性能
进行了研究[14]
ꎮ
本文采用分布式光纤布里渊传感技术开展 CFRP
板变形监测ꎬ通过在 CFRP 悬臂板上布设分布式光
纤传感器开展 CFRP 损伤前后的变形研究ꎬ并探讨
分布式光纤传感器定点布设和连续布设测试的差异
性ꎮ 为验证变形监测方法的有效性ꎬ对分布式光纤
监测数据与布设在 FRP 板上电阻应变片测量值和
ABAQUS 有限元分析值进行了对比分析ꎮ
1 分布式光纤布里渊传感原理
基于布里渊散射谱分析ꎬ布里渊散射频移与温
度和应变呈线性关系ꎬ如式(1)所示:
ΔvB
=CεΔε +CTΔT (1)
式中:Cε ꎬCT 为应变和温度灵敏度系数ꎻΔεꎬΔT 为施
加在光纤上应变和温度增量[15ꎬ16]
ꎮ 对于普通光纤
而言ꎬCε
= 0? 05 MHz/ μεꎬCT
= 1? 00 MHz/ ℃ ꎮ
由式(1) 可以看出ꎬ光纤布里渊频移对温度和
应变同时敏感ꎮ 应变测试时ꎬ温度变化 1 ℃ 会导致
约 20 με 的不确定性ꎮ 实际工程服役对象在阴晴及
季节转换时会有较大温度差ꎬ因此ꎬ实际工程应变测
试需要温度补偿ꎮ 目前常用的补偿方法是在应变传
感器附近布设一根不受外力影响的温度光纤ꎬ基于
温度测试值对应变光纤进行一一补偿ꎬ如式( 2)
所示:
Δε =(ΔvB
-ψΔvB1 ) / Cε (2)
式中:ΔvB1(ΔvB1
=CTTΔT)为仅感知温度的布里渊频
移ꎬ即分布式光纤温度传感器感知的布里渊频移ꎻ
CTT为分布式光纤温度传感器的灵敏度系数ꎻψ = CT
/
CTT为分布式光纤应变传感器和分布式光纤温度传
感器的温度灵敏度系数比值ꎬ如果分布式光纤应变
传感器和分布式光纤温度传感器的封装材料一样ꎬ
则比值为 1ꎮ
2 碳纤维复合增强板( CFRP) 变形监测模
型试验
图 1 为基于分布式光纤传感技术的碳纤维复合
增强板(CFRP)变形监测试验模型ꎬ包括分布式光纤
布里渊光时域分析系统(BOTDA)、应变采集仪、碳
纤维复合增强板(CFRP)、光纤(OF)以及电阻应变
片ꎮ BOTDA 用于分布式光纤应变测试ꎬ应变采集仪
用于点式电阻应变片测试ꎮ
图 1 CFRP 板变形监测模型
Fig? 1 Photos of CFRP model for deformation measurement
图 2 为分布式光纤和电阻应变片在 CFRP 板上
的布设位置示意图ꎮ CFRP 板尺寸为 1300 mm×50
mm×3? 2 mm(长×宽×高)ꎬ分布式光纤 OF1 为两端
定点固定在 CFRP 板表面ꎻ分布式光纤 OF2 通过 AB
胶连续粘贴在 CFRP 板表面ꎻOF1 和 OF2 平行相距
10 mmꎮ 为验证分布式光纤传感器应变测试的有效
性ꎬ在 CFRP 板表面离散布设 8 个电阻应变片ꎬ其中
Es1、Es2、Es3 和 Es4 分别距离 CFRP 板固定端 10 cm、
35 cm、60 cm 和 110 cmꎻEs1 和 Es5ꎬEs2 和 Es6ꎬEs3
和 Es7ꎬEs4 和 Es8 分别对称布设ꎬ具体布设位置如
图 2 所示ꎮ
2021 年第 12 期 49
???????????????????????????????????????????????
基于分布式光纤传感技术的 CFRP 板变形监测研究
图 2 传感器布设示意图
Fig? 2 Schematic diagram of sensor arrangement
CFRP 板单端固支ꎬ固支长度为 10 cmꎻ另一端
悬挂重物ꎮ 试验工况分为 CFRP 板无损工况和有损
工况ꎮ CFRP 板无损状态开展加载试验ꎬ每次试验
荷载步为 100 gꎬ最大荷载为 500 gꎮ 每加一级荷载ꎬ
BOTDA 采集 OF1 和 OF2 上的分布式光纤布里渊频
移ꎬ应变采集仪采集离散的电阻应变值ꎮ 损伤工况
为在 CFRP 板距端部位置 30 cm 开 2 条尺寸为 10
mm×3? 2 mm 的槽ꎬ然后进行步长为 100 g 的加载ꎬ
最大荷载为 700 gꎮ 本试验中 BOTDA 空间分辨率为
50 cmꎬ应变测量精度为± 20 μεꎬ采样点间距为 10
cmꎮ 试验在室内进行ꎬ环境温度基本保持恒定ꎬ应
变测试不考虑温度补偿ꎮ
3 试验结果分析
图 3 为 CFRP 板无损工况下基于 ABAQUS 软件
的有限元建模ꎬCFRP 板单端固支ꎬ另一端部受竖向
荷载ꎮ CFRP 板弹性模量为 55 GPaꎬ单元类型为
C3D8R 单元(八结点线性六面体单元ꎬ减缩积分)ꎬ
节点数为 10440 个ꎬ单元数为 7020 个ꎮ
(a)CFRP 板单端约束
(a)Single end restraint of CFRP plate
(b)CFRP 板网格划分
(b)Meshing of CFRP plate
图 3 CFRP 板有限元建模
Fig? 3 Finite element modeling of CFRP plate
图 4 和图 5 分别为 CFRP 板承受 500 g 荷载作用ꎬ
无损和有损工况下 CFRP 板有限元分析结果ꎮ 有损
工况下节点数为 11468 个ꎬ单元数为 7776 个ꎮ
图 4 无损工况下ꎬ500 g 作用下 CFRP 板变形云图
Fig? 4 Deformation nephogram of CFRP plate with
out damage under 500 g load
图 5 损伤工况下ꎬ500 g 作用下 CFRP 板变形云图
Fig? 5 Deformation nephogram of CFRP plate with
damage under 500 g load
图 6 为无损工况下ꎬ各级荷载作用下 CFRP 板
上 OF1 和 OF2 的布里渊频移 3D 分布ꎮ 因 OF1 两端
固定ꎬ为轴向拉伸ꎬ应变数据为 OF1 长度内的平均
应变ꎻOF2 为全粘贴在 CFRP 板上ꎬ所以 OF1 的布里
渊曲线要比 OF2 的布里渊曲线平坦ꎮ 图 7 为各级荷
载作用下ꎬCFRP 板上分布式光纤传感器测量应变
和理论应变(有限元分析应变) 的对比情况ꎮ 表 1
为 500 g 荷载作用下ꎬ分布式光纤传感器 OF1、OF2、
离散应变片测量应变与有限元分析得到的应变的对
比情况ꎮ 表中位置表示距离 CFRP 板固定端的距
离ꎬ应变片 1 表示 Es1、Es2、Es3 和 Es4ꎬ应变片 2 表
示 Es4、Es5、Es6 和 Es7ꎮ
(a)OF1
50 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
(b)OF2
图 6 各级荷载作用下 OF1 和 OF2 的布里渊频移
3D 示意图(CFRP 板无损工况)
Fig? 6 3D diagram of Brillouin frequency shift of OF1 and OF2
under different level loads (CFRP plate without damage)
(a)OF1
(b)OF2
图 7 各级荷载作用下分布式光纤传感器测量应变和
理论应变对比(CFRP 板无损工况)
Fig? 7 Strain comparison between OFs and FEM under
different level loads (CFRP plate without damage)
表 1 分布式光纤传感器 OF1、OF2、
应变片测量应变与有限元应变的对比
Table 1 Strain comparison of distributed optical
fiber sensorsꎬ ES and finite element strain
位置
/ cm
应变片 1
/ με
应变片 2
/ με
OF1
/ με
OF2
/ με
FEM
/ με
10 1163 1041 1182 1018 1031
35 767 759 796 709 750
60 549 567 708 516 562
110 233 223 220 122 93
可以看出ꎬ与 OF1 相比ꎬOF2 测量的应变值更接
近有限元分析得到的应变值ꎮ BOTDA 空间分辨率
为 50 cmꎬ因此理论上来说有限元分析得到的应变值
要大于分布式光纤传感器测量的应变值ꎮ 在 CFRP
板自由端附近ꎬ各级荷载作用下分布式光纤传感器
测量的应变值在有限元分析值附近上下波动ꎬ主要
原因是 CFRP 板自由端应变小ꎬ而 BOTDA 有一定的
测试误差ꎬ所以 OF2 误差的正负增量导致了应变测
量值的波动性ꎮ OF2 测量的应变要大于 OF1 和
FEM 分析应变ꎬ主要原因是 OF1 测量的是 CFRP 变
形时整体平均应变ꎮ 从图 6 的试验结果可以看出ꎬ
OF2 测量值反映了 CFRP 板连续变形ꎮ
图 8 为 CFRP 板损伤工况下ꎬ各级荷载作用下
CFRP 板上 OF1 和 OF2 的布里渊频移 3D 分布ꎬ依然
可以看出 OF1 的布里渊频移图要比 OF2 的布里渊频
移图平坦ꎮ 图 9 为各级荷载作用下ꎬ带损伤的 CFRP
板上分布式光纤传感器测量应变和理论应变(有限元
分析应变)的对比情况ꎮ 可以明显看出ꎬ在 CFRP 板
损伤位置ꎬ有限元分析得到的应变曲线和 OF2 测量曲
线均有一个突变点ꎮOF1 测量的应变曲线没有识别出
损伤ꎬ主要原因是 OF1 测试的是 CFRP 板的整体平均
应变ꎬ而 CFRP 自由端附近虽然有损伤ꎬ但是本身因
损伤导致的应变比较小ꎮ 同样可以看出ꎬOF2 测量的
应变要比 OF1 测量的应变更为接近 FEM 分析应变ꎮ
(a)OF1
(b)OF2
图 8 各级荷载作用下ꎬOF1 和 OF2 的布里渊频移
3D 示意图(CFRP 板损伤工况)
Fig? 8 3D diagram of Brillouin frequency shift of OF1 and OF2
under different level loads (CFRP plate with damage)
2021 年第 12 期 51
???????????????????????????????????????????????
基于分布式光纤传感技术的 CFRP 板变形监测研究
(a)OF1
(b)OF2
图 9 各级荷载作用下ꎬ分布式光纤传感器测量应变和
理论应变对比(CFRP 板损伤工况)
Fig? 9 Strain comparison between OFs and FEM under
different level loads (CFRP plate with damage)
4 结 论
本文在 CFRP 板表面连续和定点布设分布式光
纤传感器ꎬ基于布里渊光纤传感技术开展 CFRP 板
变形监测研究ꎬ并通过有限元分析和离散应变片对
比研究分布式光纤传感器测试的有效性ꎮ 所得主要
结论如下:
(1)分布式光纤传感器可以获取 CFRP 板表面
连续的应变或变形分布ꎬ测量的连续应变与局部应
变片测量值、ABAQUS 有限元分析值基本一致ꎮ
(2)分布式光纤传感器布设在 CFRP 板表面时ꎬ
连续布设比定点布设更能反映 CFRP 板的真实变
形ꎬ且在此监测试验中ꎬ分布式光纤传感器连续布设
能够识别 CFRP 板损伤ꎬ定点布设工况中ꎬ由于两个
定点距离较长ꎬ损伤信息被其他位置信息给平均化
处理掉了ꎬ因此不能有效识别损伤ꎮ
参考文献
[1] 王磊ꎬ 李威ꎬ 陈爽ꎬ 等. 海水浸泡对 FRP 筋 ̄珊瑚混凝土粘结性
能的影响[J]. 复合材料学报ꎬ 2018ꎬ 35(12): 3458 ̄3465.
[2] 杜云兴ꎬ 侯春旭ꎬ 周芬. 不均匀胶层对 CFRP 板加固梁的界面应
力影响[J]. 湖南大学学报(自然科学版)ꎬ 2017ꎬ 44(3): 61 ̄67.
[3] 宗俊达ꎬ 姚卫星. FRP 复合材料剩余刚度退化复合模型[ J]. 复
合材料学报ꎬ 2016ꎬ 33(2): 280 ̄286.
[4] 李水扬ꎬ 李峰ꎬ 马青那ꎬ 等. 动态监测技术在 FRP 试验中的应用
[J]. 现代交通技术ꎬ 2015ꎬ 12(5): 35 ̄39.
[5] 蔚道祥ꎬ 杨宇清ꎬ 鲁洪亮ꎬ 等. 声发射检测技术在 FRP 复合材料
容器检测中的应用研究[J]. 广州化工ꎬ 2019ꎬ 47(14): 152 ̄153.
[6] 李伟ꎬ 王宇ꎬ 吴超群ꎬ 等. 基于声发射检测技术的 FRP 复合材料
损伤试验研究[J].化工机械ꎬ 2011ꎬ 38(6): 692 ̄696.
[7] SCHULTE Kꎬ BARON C. Load and failure analysis of CFRP lami ̄
nates by means of electrical resistivity measurements[J]. Composites
Science and Technologyꎬ 1989ꎬ 36(1): 63 ̄65.
[8] 蒋园园. 光纤光栅传感器应用于复合材料损伤监测的研究[D].
武汉: 武汉理工大学ꎬ 2012.
[9] 吴慧峰. 基于光纤光栅传感技术的机翼形变测量方法研究与分
析[J]. 桂林航天工业学院学报ꎬ 2017ꎬ 4: 359 ̄364.
[10] 李小伟. 基于光纤光栅传感技术的风机叶片检测研究[D]. 南
京: 南京航空航天大学ꎬ 2013.
[11] XU Jꎬ HE J Pꎬ ZHANG L. Collapse prediction of karst sinkhole via
distributed Brillouin optical of sensor[J]. Measurementꎬ 2017ꎬ 100:
68 ̄71.
[12] CHEN H Jꎬ HE J Pꎬ XUE Yꎬ et al. Experimental study on sinkhole
collapse monitoring based on distributed Brillouin optical fiber
sensor[J]. Optikꎬ 2020ꎬ 216(164825): 1 ̄10.
[13] WANG H Pꎬ NI Y Qꎬ DAI J Gꎬ et al. Interfacial debonding detec ̄
tion of strengthened steel structures by using smart CFRP ̄FBG com ̄
posites[ J]. Smart Materials and Structuresꎬ 2019ꎬ 28( 115001):
1 ̄13.
[14] WANG H Pꎬ DAI J G. Strain transfer analysis of fiber Bragg grating
sensor assembled composite structures subjected to thermal loading
[J]. Composites Part B: Engineeringꎬ 2019ꎬ 162: 303 ̄313.
[15] CULVERHOUSE Dꎬ FARAHI F. Potential of stimulated Brillouin
scattering as sensing mechanism for distributed temperature sensors
[J]. Electronics Lettersꎬ 1989ꎬ 25: 913 ̄915.
[ 16] HORIGUCHI Tꎬ KURASHIMA Tꎬ TATEDA M. A technique to
measure distributed strain in optical fibers [ J]. IEEE Photonics
Technology Lettersꎬ 1990ꎬ 2(5): 352 ̄354.
52 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 008
磁致取向碳纳米管增强玻璃纤维 / 环氧复合材料的层间性能研究
黄东辉1ꎬ2
ꎬ 曾少华2∗
(1? 安徽森泰木塑集团股份有限公司ꎬ 广德 242200ꎻ 2? 安徽大学 化学化工学院ꎬ 合肥 230601)
摘要: 为提升玻璃纤维/ 环氧复合材料(GFRE)的层间性能ꎬ本文采用共价键合的方式将四氧化三铁(Fe3O4 )纳米磁球负
载于多壁碳纳米管(MWCNTs)表面得到 Fe3O4@MWCNTs 纳米粒子ꎬ再将其通过三辊研磨、超声分散于环氧树脂中ꎬ并利用弱
磁场诱导制备含取向 MWCNTs 的玻璃纤维/ 环氧复合材料ꎮ 结果表明:弱磁场作用下 MWCNTs 沿树脂流动方向取向分布ꎬ并
且 MWCNTs 和 Fe3O4在树脂中具有协同助分散的作用ꎬ取向且分散均匀的 MWCNTs 能够增强与增韧复合材料层间区域ꎬ实现
复合材料力学性能和热性能的提升ꎻ相比于纯 GFREꎬ含取向 MWCNTs 复合材料的层间剪切强度和断裂功分别提升约 31%和
117%ꎬ拉伸、弯曲性能及储能模量都有明显提升ꎬ且玻璃化转变温度提高了约 7 ℃ ꎮ
关键词: 纤维增强复合材料ꎻ 环氧树脂ꎻ 碳纳米管ꎻ 取向ꎻ 层间剪切强度
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0053-07
Interlaminar properties of magnetically oriented carbon nanotubes ̄reinforced glass fiber /epoxy composites
HUANG Dong ̄hui
1ꎬ2
ꎬ ZENG Shao ̄hua
2∗
(1? Anhui Sentai Wood Plastic Group Co.ꎬ Ltd.ꎬ Guangde 242200ꎬ Chinaꎻ
2? College of Chemistry & Chemical Engineeringꎬ Anhui Universityꎬ Hefei 230601ꎬ China)
Abstract:To improve the interlaminar properties of glass fiber reinforced epoxy composites (GFRE)ꎬ ferroferric
oxide@multi ̄walled carbon nanotubes nanoparticles (Fe3O4@MWCNTs) were prepared by depositing Fe3O4
on the
surface of MWCNTs based on the covalent bondingꎬ and then such nanoparticles were dispersed in epoxy resin by
three ̄roll grinding and ultrasound methods. The glass fiber/epoxy composites containing oriented MWCNTs were fab ̄
ricated under a weak magnetic field. The results showed that MWCNTs were distributed along the flow direction of
resins under a weak magnetic fieldꎬ and MWCNTs and Fe3O4
could promote mutual co ̄dispersion in resins. MWC ̄
NTs with uniform orientation and dispersion could strengthen and toughen the interlaminar region of compositesꎬ and
the improved mechanical and thermal properties of composites could be realized. Compared with pure GFREꎬ the in ̄
terlaminar shear strength and work of fracture of composites containing oriented MWCNTs were increased by about
31% and 117%ꎬ respectively. The tensile and flexural properties and storage moduli were significantly improvedꎬ
and the glass transition temperature was increased by about 7 ℃ .
Key words:fiber ̄reinforced compositesꎻ epoxy resinꎻ carbon nanotubesꎻ orientationꎻ interlaminar shear strength
收稿日期: 2021 ̄04 ̄13
基金项目: 安徽省高等学校自然科学研究重点项目 (KJ2020A0015)ꎻ 安徽大学博士科研启动经费 (S020318008 / 003)
作者简介: 黄东辉 (1972 ̄)ꎬ 男ꎬ 学士ꎬ 高级工程师ꎬ 主要从事高分子复合材料成型工艺方面的研究ꎮ
通讯作者: 曾少华 (1990 ̄)ꎬ 男ꎬ 博士ꎬ 讲师ꎬ 主要从事纤维增强复合材料表界面改性及功能化应用方面的研究ꎬ shzeng@ahu? edu? cnꎮ
1 前 言
玻璃纤维增强聚合物基复合材料(GFRP)具有
比强度和比模量高、可设计性强、耐腐蚀性好等优
点ꎬ已被广泛应用于民用基础设施领域[1ꎬ2]
ꎮ 但在
需要承受较大弯曲应力或高剪切力的应用场合ꎬ
GFRP 往往出现层间破坏现象ꎬ导致结构寿命缩短
或失效ꎮ 为了抑制分层破坏ꎬ常采用三维编织、Z ̄
pinning 技术、缝合等方法提高 GFRP 层间性能[3ꎬ4]
ꎮ
然而这些技术大多存在工艺局限性、性能提升有限
及成本较高等问题ꎮ 采用蒙脱土、碳纳米管、石墨烯
等纳米材料填充树脂基体是现阶段使用最广泛的
GFRP 层间性能强化方式[5 ̄7]
ꎮ 其中ꎬ碳纳米管以其
优良的力学、电学、热学等特性成为复合材料的理想
增强填料之一ꎬ将其引入 GFRP 体系符合高性能复
2021 年第 12 期 53
???????????????????????????????????????????????
磁致取向碳纳米管增强玻璃纤维/ 环氧复合材料的层间性能研究
合材料低成本制造的发展方向[8]
ꎮ
碳纳米管具有高长径比和高比表面积ꎬ其轴向
性能远远优于径向性能ꎮ 通过调控碳纳米管在 GFRP
厚度方向的取向状态ꎬ可有效提升 GFRP 的层间性
能ꎮ 目前ꎬ在 GFRP 中置入取向碳纳米管的方法有
两种:一是以玻纤为模版ꎬ通过化学气相沉积法在玻
纤表面生长定向碳纳米管ꎬ再与纯树脂通过手糊、树
脂传递模塑等成型工艺制备复合材料[9]
ꎻ二是将碳
纳米管分散于树脂中ꎬ利用物理场(流场、电场、磁场
等)使碳纳米管在树脂中取向排列[10]
ꎮ 前者工艺需
要在玻纤表面负载催化剂ꎬ后处理难以除净ꎬ且生长
碳纳米管一般需要高温(>500 ℃ )ꎬ这种高温反应环
境容易损伤玻纤力学性能[11]
ꎮ 利用电、磁场诱导碳
纳米管的有序排列逐渐受到青睐ꎮ 如董怀斌等[12] 利
用高频电场诱导法制备了多壁碳纳米管(MWCNTs)
定向排列的碳纤维/ 环氧复合材料ꎬMWCNTs 的定向
排列有效提升了复合材料的力学性能ꎮ 为了提高碳
纳米管磁性ꎬ研究者多采用磁性粒子改性碳纳米管ꎬ
再利用磁场诱导碳纳米管在树脂中取向或定向[13ꎬ14]
ꎮ
但这些研究主要集中于碳纳米管改性聚合物复合材
料ꎬ很少涉及碳纳米管有序增强 GFRP 层间性能ꎮ
针对 GFRP 层间性能不足的问题ꎬ本文先将 Fe3O4
纳米磁球负载于多壁碳纳米管(MWCNTs)表面得到
Fe3O4@MWCNTsꎬ然后将其通过三辊研磨、超声分散
于环氧树脂中ꎻ将混合树脂通过手糊涂覆于玻纤织
物中ꎬ再先后置于真空袋和弱磁场中得到含取向
MWCNTs 的玻纤/ 环氧复合材料ꎮ 重点研究弱磁场诱
导取向 MWCNTs 对 GFRP 微观结构及层间性能的影
响ꎬ探讨了取向 MWCNTs 对复合材料层间增强机理ꎮ
2 实验部分
2? 1 主要原料
羧基化 MWCNTs(工业级ꎬ直径为 20 nm~40 nmꎬ
长度约为 30 μm)为中国科学院成都有机化学有限
公司生产ꎻE ̄玻纤织物(纤维直径约为 17 μmꎬ面密
度为 1200 g / m
2
)、环氧树脂(LY1564ꎬ25 ℃下黏度为
1200 mPa?s~1400 mPa?s)及其固化剂(A3486ꎬ25 ℃下
黏度为 10 mPa?s~20 mPa?s)均由连云港中复连众
复合材料集团有限公司提供ꎻFe3O4纳米磁球(直径
约为 50 nm) 和钕铁硼磁铁(磁感应强度约为 3500
Gs)分别购于杭州恒纳新材料有限公司和无锡申磁
磁业有限公司ꎻγ ̄氨丙基三乙氧基硅烷(KH550)、
NꎬN ̄二异丙基碳二亚胺( DIC)、 1 ̄羟基苯丙三唑
(HOBT)、二甲基亚砜(DMSO)、无水乙醇等均购自
南京化学试剂股份有限公司ꎮ
2? 2 样品制备
2? 2? 1 Fe3O4@MWCNTs 的制备
将 DIC、HOBT、KH550和 MWCNTs(质量比为 0? 01 ∶
0? 01 ∶ 0? 01 ∶1)分别加入溶剂 DMSO 中ꎬ超声 30 min 后
机械搅拌 6 hꎬ将混合液静置、离心ꎬ倒掉上层清液并用
无水乙醇清洗 2 次~3 次ꎬ得到 KH550 改性 MWCNTsꎻ
然后ꎬ将其与 Fe3O4(质量比为 Fe3O4
∶MWCNTs = 1∶4)
分散于无水乙醇中ꎬ超声 10 min 后向混合液中滴加
去离子水(质量比为去离子水 ∶无水乙醇= 4 ∶96)ꎬ保
持搅拌 10 min 后离心去除上层清液ꎬ100 ℃ 真空干
燥后得到 Fe3O4@MWCNTs(制备过程见图 1)ꎮ
图 1 Fe3O4@MWCNTs 制备工艺示意图
Fig? 1 Schematic diagram of preparation process
of Fe3O4@MWCNTs
2? 2? 2 取向 MWCNTs 复合材料的制备
裁剪玻纤织物(尺寸为 250 mm×150 mm)ꎬ并分别
计算称量 LY1564 和 A3486 待用( LY1564 ∶A3486 =
100 ∶ 34)ꎮ 按照 LY1564 和 A3486 总质量计ꎬ称取
0? 5wt%的 Fe3O4@MWCNTs 加入 LY1564 中ꎬ经机械
搅拌 2 h、三辊研磨 2 min~4 min 后加入 A3486ꎬ搅拌
均匀后真空脱气泡得到 MWCNTs 混合液ꎻ然后ꎬ将
其通过手糊ꎬ均匀地涂覆于玻璃纤维织物中ꎬ再置于
真空袋中抽真空除空气ꎬ同时将钕磁铁放置在真空
袋上下表面ꎻ最后经室温固化 24 h、70 ℃下后固化 6
h 得到取向 MWCNTs 增强玻纤/ 环氧复合材料(记为
Fe@M ̄m ̄GFRE)ꎮ 类似上述步骤ꎬ分别将 0? 5wt%的
54 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
MWCNTs、Fe3O4@MWCNTs 置于磁场及无磁场环境
中制备复合材料ꎬ分别记为 M ̄m ̄GFRE 和 Fe@M ̄n ̄
GFREꎮ此外ꎬ制备纯 GFRE 作为空白试样ꎮ
2? 3 测试与表征
利用傅里叶红外光谱仪(FTIRꎻVertex 80vꎬBrukerꎬ
德国)分析纳米粒子的化学结构ꎮ 分别通过场发射
扫描电子显微镜( SEMꎻInspect F50ꎬFEIꎬ美国)和 X
射线能谱仪(EDXꎻOctane SuperꎬEDAXꎬ美国) 表征
Fe3O4@MWCNTs 粉末的表面形貌及元素分布ꎮ 将复
合材料分层后ꎬ选择树脂基体富集区域采用超薄切
片机(EM UC7ꎬLeicaꎬ德国)进行切片ꎬ并利用透射电
子显微镜(TEMꎻJEM ̄1400ꎬJEOLꎬ日本)观察复合材
料中 MWCNTs 分散及定向状态ꎮ
复合材料的力学性能皆利用电子万能试验机
(CMT ̄5105ꎬSANSꎬ中国) 测试ꎬ拉伸性能测试参照
GB/ T 1447—2005ꎬ试样尺寸为 2 mm×25 mm×150 mmꎬ
加载速度为 2? 0 mm / minꎻ弯曲性能测试参照 GB / T
1449—2005ꎬ试样尺寸为 2 mm×15 mm×40 mmꎬ跨距
为 32 mmꎬ加载速度为 2? 0 mm / minꎻ层间剪切性能
测试参照 ISO 14130—1997ꎬ试样尺寸为 4 mm × 20
mm× 40 mmꎬ跨距为 16 mmꎬ加载速度为 1? 0 mm /
minꎮ 采用表面电阻测试仪(SL ̄030Bꎬ无锡欣律图防
静电设备有限公司ꎬ中国)测试表面电阻ꎮ 复合材料
的动态力学热性能采用动态力学热分析仪(Q800ꎬ
TAꎬ美国)测试ꎬ试样尺寸为 2 mm×10 mm×60 mmꎬ
采用三点弯曲模式在空气氛围下以 5 ℃ / min 的速
率从室温升至 180 ℃ ꎬ频率为 1 Hzꎮ
3 结果与讨论
3? 1 Fe3O4@MWCNTs 的结构与形貌
图 2 为 Fe3O4@MWCNTs、Fe3O4和 MWCNTs 三种
粉末的红外光谱图ꎮ 在 3423 cm
-1处ꎬFe3O4@MWCNTs
出现的是仲胺( -NH-)伸缩振动峰ꎬ而 MWCNTs 和
Fe3O4呈现为强烈的羟基( -OH)伸缩振动峰ꎮ 加入
KH550 后ꎬFe3O4@MWCNTs 在 2930 cm
-1及 2867 cm
-1
处出现较强的亚甲基(-CH2
-)对称伸缩振动峰及反
对称伸缩振动峰ꎬ1165 cm
-1处表现为碳氮键(C-N)
的特征峰ꎻ而 1029 cm
-1处为硅氧键( Si-O-Si)伸缩
振动峰ꎮ 另外ꎬ1662 cm
-1 处为羰基(C = O) 的特征
峰ꎮ因此ꎬKH550 通过酰胺化反应及水解缩合使 Fe3O4
与 MWCNTs 二者间实现共价键连接ꎮ
图 2 Fe3O4@MWCNTs、Fe3O4和
MWCNTs 的红外光谱图
Fig? 2 FTIR spectra of Fe3O4@MWCNTsꎬ
Fe3O4
and MWCNTs
图 3 为 Fe3O4@MWCNTs 的结构及微观形貌ꎮ 如
图 3(a)和图 3(b)所示ꎬFe3O4磁球吸附于 MWCNTs
表面ꎬ且 MWCNTs 分散相对均匀ꎮ 由图 3(c)可见ꎬ除
Fe3O4和 MWCNTs 基本的铁元素和碳元素外ꎬ新出
现硅元素、氮元素及铁元素主要源于 KH550ꎮ 这进
一步证实了 Fe3O4通过共价键连接于 MWCNTs 表面ꎮ
图 3 Fe3O4@MWCNTs 的 SEM 图(a)、
TEM 图(b)及 EDX 能谱图(c)
Fig? 3 SEM (a)ꎬ TEM (b) images and EDX spectrum (c)
of Fe3O4@MWCNTs
3? 2 MWCNTs 取向机理分析
图 4 为 Fe3O4@MWCNTs 分散水溶液的磁响应
变化ꎮ 图 4 中的(1)和(2)分别为 MWCNTs 和 Fe3O4
@MWCNTs 分散液ꎮ 由图 4 可见ꎬ在超声分散后立即
放置于磁铁石旁边ꎬ两种分散液都为表面分散均匀
的状态ꎬ但在静置 40 s 后ꎬFe3O4@MWCNTs 分散液
中出现黑色粉体靠近磁铁石沿着试管壁集聚的现
2021 年第 12 期 55
???????????????????????????????????????????????
磁致取向碳纳米管增强玻璃纤维/ 环氧复合材料的层间性能研究
象ꎬ而 MWCNTs 分散液则无明显的变化ꎮ 这说明负
载 Fe3O4纳米粒子的 MWCNTs 在施加磁场的环境中
会表现出一定的顺磁性ꎮ
图 4 Fe3O4@MWCNTs 分散液磁响应数码照片
Fig? 4 Digital photo of magnetic response of
Fe3O4@MWCNTs dispersions
利用 MWCNTs 轴向电导率远大于径向电导率的
性质ꎬ可通过测试复合材料表面电阻来评估 MWCNTs
的取向情况ꎮ 图 5 所示为含 MWCNTs 复合材料在平
行与垂直树脂流动方向的表面电阻ꎮ 由图可见ꎬ含
MWCNTs 复合材料在平行树脂流动方向的表面电阻
下降明显ꎬ尤其是 Fe@M ̄m ̄GFRE 在平行树脂流动
方向和垂直流动方向的表面电阻差值最大ꎮ 由此可
推断ꎬ施加磁场制备的 Fe@M ̄m ̄GFRE 中 MWCNTs
表现出取向特征ꎮ
图 5 含 MWCNTs 复合材料的表面电阻
Fig? 5 Surface resistance of composites containing MWCNTs
为进一步表征 MWCNTs 取向效果ꎬ采用 TEM
对复合材料层间区域的树脂基体进行测试ꎬ如图 6
所示ꎮ 相比于 M ̄n ̄GFREꎬ含 Fe3O4@MWCNTs 复合
材料中 MWCNTs 都相对均匀ꎬ说明负载 Fe3O4纳米
磁球有助于提升 MWCNTs 的分散性ꎮ 而相比于 Fe
@M ̄n ̄GFREꎬFe@M ̄m ̄GFRE 中的 MWCNTs 具有取
向分布ꎬ如图 6( c) 中白色箭头方向所示ꎮ 这说明
Fe3O4 纳米磁球有助于 MWCNTs 在磁场下取向与
分散ꎮ
图 6 MWCNTs 复合材料中分散的 TEM 图
Fig? 6 TEM images of MWCNTs dispersion state in composites
3? 3 复合材料的层间剪切性能
碳纳米管的分散及取向对复合材料的力学性能
有重要影响ꎮ 图 7 为含 MWCNTs 复合材料的层间
剪切荷载 ̄位移曲线及层间剪切性能ꎮ
(a)
(b)
图 7 含 MWCNTs 复合材料的层间剪切荷载 ̄位移
曲线(a)及层间剪切强度和断裂功(b)
Fig? 7 Load ̄deflection curves (a) and ILSS and work of
fracture (b) of composites containing MWCNTs
56 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
由图 7( a) 可知ꎬ相比于纯 GFREꎬ含 MWCNTs
复合材料的层间剪切荷载明显增加ꎬ且到达峰值后
仍保持缓慢降低的趋势ꎬ说明 MWCNTs 能够提升复
合材料的层间性能ꎻ进一步地ꎬFe@M ̄n ̄GFRE 和 Fe
@M ̄m ̄GFRE 的层间剪切荷载峰值及位移都高于 M ̄
m ̄GFREꎬ说明 MWCNTs 和 Fe3O4对复合材料层间剪
切性能具有协同增强的效果ꎮ
断裂功(即荷载 ̄位移曲线面积)可被用于衡量
复合材料的层间断裂韧性[15]
ꎮ 如图 7( b) 所示ꎬFe
@M ̄m ̄GFRE 的层间剪切强度和断裂功都拥有最大
值ꎬ且其层间剪切强度和断裂功较之纯 GFRE 分别
提升 30? 7%和 117? 1%ꎬ断裂功提升最明显ꎮ 取向
MWCNTs 不仅改善了复合材料的层间黏合强度ꎬ还
提升了复合材料的层间断裂韧性ꎮ
取向 MWCNTs 对复合材料层间断裂韧性的影
响还可进一步通过层间断裂形貌证实ꎬ如图 8 所示ꎮ
纯 GFRE 的层间剪切断面平整ꎬ且纤维表面光滑ꎬ含
有极少量的树脂ꎬ见图 8( a)ꎬ这表现出脆性断裂现
象ꎮ 由图 8(b) ~图 8(d)可见ꎬMWCNTs 复合材料层
间剪切断面相对粗糙ꎬ且纤维表面黏附更多的树脂
碎片ꎬ尤其是 Fe @ M ̄m ̄GFRE 表面更加明显ꎮ 但
M ̄m ̄GFRE表面含有少量 MWCNTs 团聚体ꎮ 结合图
3 和图 8 可说明ꎬFe3O4纳米球不仅赋予了 MWCNTs
一定的顺磁性ꎬ使之顺利取向ꎬ还有助于提高 MWCNTs
在树脂中的分散性ꎬ两者协同作用下实现了复合材
料层间黏合性及断裂韧性的提升ꎮ
图 8 含 MWCNTs 复合材料的层间剪切断面
Fig? 8 Interlaminar shear fracture surfaces of
composites containing MWCNTs
3? 4 复合材料的拉伸和弯曲性能
图 9 为含 MWCNTs 复合材料的拉伸和弯曲性能ꎮ
由图9(a)和图9(b)可知ꎬ添加 MWCNTs 使复合材料的
拉伸和弯曲性能均有所提高ꎬ尤其是 Fe@M ̄m ̄GFRE
的力学性能提升最明显ꎮ 相比于纯 GFREꎬFe@M ̄m ̄
GFRE 的拉伸强度和模量分别提高了 26? 7%和 22? 1%ꎬ
弯曲强度和模量分别提高了 25? 0%和 23? 8%ꎮ 这说
明取向 MWCNTs 在复合材料受力过程中有助于传
递和消散应力ꎬ进而提升复合材料的力学性能ꎮ
(a)
(b)
图 9 含 MWCNTs 复合材料的拉伸(a)及弯曲(b)性能
Fig? 9 Tensile (a) and flexural (b) properties of
composites containing MWCNTs
3? 5 复合材料的动态力学热性能
含 MWCNTs 复合材料的储能模量和损耗因子
随温度的变化分别如图 10(a)和图 10(b)所示ꎮ 表
1 列出了含 MWCNTs 的复合材料在 30 ℃ 和 180 ℃
时的储能模量(分别记为 E30
′和 E180
′)、玻璃化转变
温度(Tg)和损耗因子峰值(Tanδmax)ꎮ
(a)
2021 年第 12 期 57
???????????????????????????????????????????????
磁致取向碳纳米管增强玻璃纤维/ 环氧复合材料的层间性能研究
(b)
图 10 含 MWCNTs 复合材料的储能模量(a)及
损耗因子(b)随温度的变化曲线
Fig? 10 Storage modulus (a) and loss factor (b) via
temperature curves of composites containing MWCNTs
表 1 含 MWCNTs 复合材料的储能模量、
玻璃化转变温度和损耗因子峰值
Table 1 Storage modulusꎬ Tg
and Tanδmax
of composites containing MWCNTs
试样编号 E30
′/ GPa E180
′/ GPa Tg
/ ℃ Tanδmax
GFRE 27.6 5.46 82.7 0.23
M ̄m ̄GFRE 28.0 6.92 84.2 0.19
Fe@M ̄n ̄GFRE 28.9 7.49 87.2 0.17
Fe@M ̄m ̄GFRE 29.9 8.08 89.3 0.16
由图 10(a)和表 1 可知ꎬ含 MWCNTs 复合材料在
玻璃态和橡胶态的储能模量都高于纯 GFREꎬ且其
在玻璃化转变区域储能模量下降趋势较之纯 GFRE
更加缓慢ꎻ取向 MWCNTs 增强复合材料的储能模量
提升最明显ꎮ 相比于纯 GFREꎬFe@ M ̄m ̄GFRE 的
E30
′和 E180
′分别提升了 8? 3%和 48? 0%ꎮ 分析可知ꎬ取
向 MWCNTs 提高了纤维与树脂之间的界面交互作
用ꎬ降低了纤维附近环氧分子链的流动性ꎬ导致复合
材料的储能模量明显提高ꎻ并且取向 MWCNTs 在复
合材料橡胶态中由取向转向无规状态需要更多的能
量ꎬ使其复合材料具有高温保持性ꎮ
由于 MWCNTs 在复合材料中占据着一定的自由
体积ꎬ限制了环氧分子链的运动ꎬ这就需要更高的温
度才能提供更充足的空间ꎬ使环氧分子链解冻ꎬ进而
导致复合材料的 Tg升高ꎮ 由表 1 可知ꎬFe@M ̄m ̄GFRE
的 Tg值最大ꎬ且较之纯 GFRE 提高了约 7 ℃ ꎮ 这说
明取向 MWCNTs 更有利于提升复合材料的耐热性ꎮ
此外ꎬ相比于纯 GFREꎬFe@M ̄m ̄GFRE 的 Tanδmax值
降低最明显ꎬ且较之纯 GFRE 下降了 30? 4%ꎮ 这进
一步证实取向 MWCNTs 提升了复合材料的层间黏
合性ꎮ
4 结 论
本文将 Fe3O4负载多壁碳纳米管(Fe3O4@MWC ̄
NTs)采用三辊研磨和超声分散于环氧树脂中ꎬ通过
手糊及抽真空工艺将混合树脂与玻璃纤维织物复
合ꎬ再在弱磁场诱导下制备含取向 MWCNTs 的复合
材料ꎻ重点研究取向 MWCNTs 对复合材料层间性能
的影响ꎮ 结果表明:
(1)Fe3O4纳米磁球有助于提高 MWCNTs 的顺
磁性及其在树脂中的分散性ꎬ实现 MWCNTs 沿树脂
流动方向取向分布ꎮ
(2)取向且分散均匀的 MWCNTs 有助于增强与
增韧复合材料层间树脂富集区域ꎻ相比于纯 GFREꎬ
含取向 MWCNTs 复合材料的层间剪切强度和断裂
功分别提升约 31%和 117%ꎮ
(3)取向 MWCNTs 能够实现复合材料力学性能
和热性能的提升ꎻ相比于纯 GFREꎬ含取向 MWCNTs
复合材料的拉伸强度和模量分别提高了约 27%和
22%ꎬ弯曲强度和模量分别提高了约 25%和 24%ꎻ储
能模量在玻璃态和橡胶态都有所提升ꎬ而且玻璃化
转变温度提高了约 7 ℃ ꎮ
参考文献
[1] 刘伟庆ꎬ 方海ꎬ 方园. 纤维增强复合材料及其结构研究进展[J].
建筑结构学报ꎬ 2019ꎬ 40(4): 1 ̄16.
[2] LIU Tꎬ FENG Pꎬ WU Yꎬ et al. Developing an innovative curved ̄
pultruded large ̄scale GFRP arch beam[ J]. Composite Structuresꎬ
2021ꎬ 256: 113111.
[ 3] COPPOLA A Mꎬ THAKRE P Rꎬ SOTTOS N Rꎬ et al. Tensile prop ̄
erties and damage evolution in vascular 3D woven glass/ epoxy com ̄
posites[J]. Composites Part A: Applied Science and Manufacturingꎬ
2014ꎬ 59: 9 ̄17.
[4] 孟令民ꎬ 周克印ꎬ 王崇高ꎬ 等. Z ̄pin 增强复合材料层合板缺陷
的红外检测技术研究[J]. 玻璃钢/ 复合材料ꎬ 2019(5): 31 ̄37.
[5] SHARMA Bꎬ CHHIBBER Rꎬ MEHTA R. Curing studies and me ̄
chanical properties of glass fiber reinforced composites based on si ̄
lanized clay minerals[J]. Applied Clay Scienceꎬ 2017ꎬ 138: 89 ̄99.
[6] 郑益飞ꎬ 申明霞ꎬ 段鹏鹏ꎬ 等. 含 MWCNTs 玻璃纤维增强复合材
料的力学和界面性能的研究[J]. 玻璃钢/ 复合材料ꎬ 2019(12):
83 ̄88.
[7] VALOROSI Fꎬ DE MEO Eꎬ BLANCO ̄VARELA Tꎬ et al. Graphene
and related materials in hierarchical fiber composites: Production
techniques and key industrial benefits [ J]. Composites Science &
Technologyꎬ 2020ꎬ 185: 107848.
[8] 汪庆卫ꎬ 吴欣ꎬ 王宏志ꎬ 等. 表面修饰碳纳米管对玻璃纤维及复
合材料的性能影响[J]. 功能材料ꎬ 2015ꎬ 46(23): 23047 ̄23050.
[9] BODDU V Mꎬ BRENNER M Wꎬ PATEL J Sꎬ et al. Energy dissipa ̄
tion and high ̄strain rate dynamic response of E ̄glass fiber composites
with anchored carbon nanotubes[J]. Composites Part B: Engineeringꎬ
58 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
2016ꎬ 88: 44 ̄54.
[10] 刘方彪ꎬ 王丹勇ꎬ 徐井利ꎬ 等. 取向碳纳米管/ 玻璃纤维增强树
脂基单向层合板的制备及其力学性能[ J]. 材料科学与工程学
报ꎬ 2015ꎬ 33(2): 163 ̄167.
[11] RAHAMAN Aꎬ KAR K K. Carbon nanomaterials grown on E ̄glass
fibers and their application in composite[J]. Composites Science &
Technologyꎬ 2014ꎬ 101: 1 ̄10.
[12] 董怀斌ꎬ 李长青ꎬ 任攀ꎬ 等. 碳纳米管定向排列增强碳纤维/ 环
氧树脂复合材料制备及力学性能[J]. 玻璃钢/ 复合材料ꎬ 2017
(7): 23 ̄29.
[13] 周还潮ꎬ 马传国ꎬ 张晶晶. 弱磁场对 EP / MWCNTs ̄Fe3 O4 复合
材料结构与性能的影响[ J]. 工程塑料应用ꎬ 2015ꎬ 43( 10):
7 ̄12.
[14] 陈伟ꎬ 郑亚萍. Fe3O4
 ̄MWCNTs 在环氧树脂中的定向排列[ J].
复合材料学报ꎬ 2013ꎬ 30(6): 54 ̄59.
[15] ZENG S Hꎬ SHEN M Xꎬ XUE Y Jꎬ et al. A novel strategy to rein ̄
force glass fiber fabric / epoxy composites via modifying fibers with
self ̄assembled multi ̄walled carbon nanotubes ̄montmorillonite[ J].
Polymer Compositesꎬ 2020ꎬ 41(2): 522 ̄534.
(上接第 24 页)
5 结 论
本文通过 6 篇文献中的 318 个复材约束海水海
砂混凝土圆柱的试验数据验证了预测其极限应力及
极限应变的 3 组代表性计算模型(Lim 模型、Wei 模
型及 Jiang 模型)的精度ꎬ得到以下结论:
(1)3 组模型在预测极限应力时的精度整体高
于预测极限应变时的精度ꎻ计算极限应力的 3 个模
型的平均绝对误差 AAE 平均值为 13? 8%ꎬ计算极限
应变的 3 个模型的 AAE 平均值为 38? 1%ꎮ
(2)Lim模型在预测极限应力时的 AAE 为10? 7%ꎬ
在预测极限应变时的 AAE 为 27? 8%ꎬ在 3 组模型中
显示出最佳精度ꎬ为预测复材约束海水海砂混凝土
极限状态的最优模型ꎮ
(3)Jiang 模型在预测极限应力时与 Lim 模型取
得相似的高精度ꎬAAE 为 11? 0%ꎬ且模型表达式简
便易算ꎬ也可用来计算复材约束海水海砂混凝土的
极限应力ꎬ但 Jiang 模型低估了极限应变ꎬ在 3 组极
限应变模型中误差最大ꎬ预测值与试验值比值的平
均值 Mean 为 52? 2%ꎮ
(4)Wei 模型对极限应力及极限应变的预测值
与试验值相比整体偏低ꎬ预测值与试验值比值的平
均值 Mean 分别为 81? 0%和 74? 5%ꎮ
参考文献
[1] 何志标. CFRP 约束海水海砂混凝土圆柱轴压力学性能研究
[D]. 广州: 广东工业大学ꎬ 2018.
[2] YANG J Lꎬ WANG J Zꎬ WANG Z R. Axial compressive behavior of
partially CFRP confined seawater sea ̄sand concrete in circular col ̄
umns ̄Part Ⅰ: Experimental study[J]. Composite Structuresꎬ 2020ꎬ
246: 112373.
[3] 曾繁新. FRP 约束模拟海砂混凝土圆柱轴压性能研究[D]. 温
州: 温州大学ꎬ 2017.
[4] 袁逸. FRP 约束模拟海水混凝土标准圆柱轴压性能研究[D]. 温
州: 温州大学ꎬ 2018.
[ 5] ZENG J Jꎬ GAO W Yꎬ DUAN Z Jꎬ et al. Axial compressive behavior
of polyethylene terephthalate / carbon FRP ̄confined seawater sea ̄
sand concrete in circular columns [ J]. Construction and Building
Materialsꎬ 2020ꎬ 234: 117383.
[6] WANG Jꎬ FENG Pꎬ HAO Tꎬ et al. Axial compressive behavior of
seawater coral aggregate concrete ̄filled FRP tubes[ J]. Construction
and Building Materialsꎬ 2017ꎬ 147: 272 ̄285.
[7] OZBAKKALOGLU Tꎬ LIM J C. Axial compressive behavior of FRP ̄
confined concrete: Experimental test database and a new design ̄ori ̄
ented model[J]. Composites Part B ̄Engineeringꎬ 2013ꎬ 55: 607 ̄634.
[8] WEI Y Yꎬ WU Y F. Unified stress ̄strain model of concrete for FRP ̄
confined columns[ J]. Construction and Building Materialsꎬ 2012ꎬ
26(1): 381 ̄392.
[9] JIANG Tꎬ TENG J G. Analysis ̄oriented stress ̄strain models for FRP ̄
confined concrete [ J]. Engineering Structuresꎬ 2007ꎬ 29 ( 11 ):
2968 ̄2986.
[10] LIM J Cꎬ OZBAKKALOGLU T. Design model for FRP ̄confined
normal ̄ and high ̄strength concrete square and rectangular columns
[J]. Magazine of Concrete Researchꎬ 2014ꎬ 66(20): 1020 ̄1035.
[11] 詹瑒ꎬ 李奔奔ꎬ 崔璟ꎬ 等. 双轴对称截面 FRP 轴心受压杆件整
体屈曲临界力计算方法分析[ J]. 复合材料科学与工程ꎬ 2021
(6): 58 ̄64.
[12] LIM J Cꎬ KARAKUS Mꎬ OZBAKKALOGLU T. Evaluation of ulti ̄
mate conditions of FRP ̄confined concrete columns using genetic
programming[J]. Computers and Structuresꎬ 2016ꎬ 162: 28 ̄37.
[13] FAM A Zꎬ RIZKALLA S H. Confinement model for axially loaded
concrete confined by circular fiber ̄reinforced polymer tubes [ J].
ACI Structural Journalꎬ 2001ꎬ 98(4): 451 ̄461.
[14] 张冰ꎬ 赵庆ꎬ 黄涛ꎬ 等. ±60°缠绕的纤维复材管约束混凝土短
柱轴压试验研究[J]. 工业建筑ꎬ 2017ꎬ 47(11): 35 ̄40ꎬ 72.
[15] 李鹏. GFRP 管约束海砂再生混凝土轴压力学性能研究[D].
青岛: 山东科技大学ꎬ 2019.
2021 年第 12 期 59
???????????????????????????????????????????????
破片和爆炸波联合加载下 UHMWPE 纤维复合材料失效行为实验研究
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 009
破片和爆炸波联合加载下 UHMWPE 纤维复合材料失效行为实验研究
苏罗川ꎬ 田立智ꎬ 宜晨虹∗
ꎬ 刘文杰ꎬ 师亚琴
(中国工程物理研究院 流体物理研究所ꎬ 绵阳 621900)
摘要: 由于超高的比拉伸强度ꎬ超高分子量聚乙烯(Ultra ̄High Molecular Weight Polyethyleneꎬ简称“UHMWPE”)纤维复合
材料在冲击防护领域获得了极大的关注ꎮ 本文通过可同时产生破片和爆炸波加载装置的设计ꎬ实验观察了 UHMWPE 纤维复
合材料在联合冲击加载下的失效行为ꎮ 实验发现ꎬUHMWPE 复合材料在联合加载下失效模式复杂ꎬ包括层间脱层、屈曲与褶
皱、侵彻穿透、纤维烧蚀等ꎮ 基于失效模式的分析ꎬ总结了 UHMWPE 纤维复合材料在破片和爆炸波联合加载下失效破坏的四
个典型阶段ꎮ
关键词: UHMWPE 复合板ꎻ 失效行为ꎻ 破片ꎻ 爆炸波
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0060-06
Experimental investigations on the failure behaviour of UHMWPE
composite panel under the loading of fragments and blast
SU Luo ̄chuanꎬ TIAN Li ̄zhiꎬ YI Chen ̄hong
∗
ꎬ LIU Wen ̄jieꎬ SHI Ya ̄qin
(Institute of Fluid Physicsꎬ China Academy of Engineering Physicsꎬ Mianyang 621900ꎬ China)
Abstract:Due to the extremely high specific strengthꎬ the ultra ̄high molecular weight polyethylene (UHM ̄
WPE) fiber reinforced laminates are widely employed in protective armors. In this paperꎬ the failure modes of UH ̄
MWPE laminate panel under explosive loading are experimentally investigated. Firstlyꎬ an explosive device that can
simultaneously produce blast and fragments is designed. And thenꎬ the deformation and failure characteristics of the
UHMWPE panel under the loading of the explosive device are gained and analyzed. The panel exhibits multiple fail ̄
ure modesꎬ including the delaminationꎬ bucklingꎬ bubblingꎬ fragments penetration and erosion. Based on the de ̄
formation characteristicsꎬ the failure progress of the UHMWPE laminate panel under explosive loading can be divid ̄
ed into four typical stages.
Key words:UHMWPE composite panelꎻ failure behaviourꎻ fragmentsꎻ blast
收稿日期: 2021 ̄04 ̄20
基金项目: 国家自然科学基金青年项目 (11602246)
作者简介: 苏罗川 (1986 ̄)ꎬ 男ꎬ 博士ꎬ 副研究员ꎬ 研究方向为轻质防护结构设计及优化ꎮ
通讯作者: 宜晨虹 (1976 ̄)ꎬ 男ꎬ 博士ꎬ 副研究员ꎬ 研究方向为冲击动力学ꎬ yichenhong@163? comꎮ
1 引 言
作为比拉伸强度最高的可用工程材料之一ꎬ超
高分子量聚乙烯纤维(Ultra ̄High Molecular Weight Po ̄
lyethyleneꎬ简称“UHMWPE”) 在冲击防护领域的应
用潜力引起了世界各国科研及工程技术人员的广泛
关注[1 ̄3]
ꎮ UHMWPE 纤维密度约为 0? 97 g / cm
3
ꎬ抗拉
强度达 GPa 量级ꎬ远优于目前常用的工程材料ꎮ 研
究表明ꎬ以聚氨酯为基质ꎬ将 10 μm ~ 20 μm 直径的
UHMWPE 纤维按照[0°/ 90°]n方向交叉铺层后热压
形成的叠层复合板(纤维的体积含量约为 85%)能展
现出极强的冲击防护性能ꎬ尤其在侵彻防护方面[4 ̄6]
ꎮ
近年来ꎬUHMWPE 复合材料在侵彻作用下的动
态响应及失效行为受到了科研人员的重点关注ꎮ
Greenhalgh 等[7] 基于实验观察揭示了 UHMWPE 复
合材料在弹体侵彻下的不同失效模式ꎬ包括层间脱
层撕裂、纤维扭曲等ꎬ同时发现复合板的损伤响应过
程与其加工过程相关ꎮ Russell 等[8] 研究认为ꎬ相比
于传统的±45
o纤维铺设方式ꎬ纤维在 0°/ 90°铺设时
复合板性能更优ꎮ Zhang 等[9] 和 Nguyen 等[10] 的实
验显示纤维的铺设方向、边界约束及板厚等因素会
较为显著地影响复合板在弹体侵彻下的变形与失
效ꎮ 而 Attwood 等[11]的工作则直接总结回答了 UH ̄
MWPE 复合板的主要侵彻防护失效机理为间接拉伸
导致的纤维断裂ꎬ即侵彻体的冲击作用使得其接触
60 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
点下方的纤维层处于压缩状态ꎬ而 UHMWPE 复合
材料内各纤维层的泊松膨胀系数在平行和垂直纤维
方向存在较大的差异ꎬ这使被压缩纤维层的侧向膨
胀引发与其垂直的相邻纤维层产生拉伸应力ꎬ当拉
伸应力达到纤维的断裂强度时ꎬ纤维开始出现断裂ꎬ
进而侵彻体继续冲击下方的纤维层ꎻ而一旦冲击带
来的压缩应力不足以引发使纤维断裂的拉应力时ꎬ
侵彻体被阻止ꎮ 这也有力解释了 UHMWPE 纤维的
高抗拉强度在其侵彻防护上的作用ꎮ
基于上述动态响应过程及侵彻防护机理的揭示ꎬ
以 UHMWPE 纤维复合材料为主体的多种侵彻防护
结构被研究人员提出ꎬ并在实验中证实了因其超高
的抗拉强度而带来的良好防护效能[12 ̄14]
ꎮ 需要指出
的是ꎬ在很多实际防护场景中(例如爆炸防护)ꎬ防
护结构会同时遭遇高速破片和爆炸波的联合冲击ꎬ
而在现有的公开报道中ꎬ少有讨论 UHMWPE 这类
防护优势材料在破片和爆炸波联合加载下的失效问
题ꎮ 因此ꎬ本文通过爆炸加载实验的设计ꎬ系统观察
了 UHMWPE 复合板在破片和爆炸波联合加载下的
失效行为ꎬ总结了复合板的主要失效模式及过程ꎮ
2 实验材料与方法
实验中的 UHMWPE 复合板采用 Dyneema 系列
的商业产品ꎮ 复合板试样的尺寸为300 mm×300 mm×
10 mm 的方形板ꎬ板材的整体密度约为 0? 98 g / cm
3
ꎮ
为模拟破片和爆炸波联合加载的情形ꎬ实验采
用图 1 所示的爆炸加载装置ꎮ 装置由钢质柱形外壳
内填充 TNT 炸药组成ꎬ在柱形炸药的两端面用雷管
同时起爆ꎬ内部炸药起爆后驱动钢质外壳运动从而
产生破片和爆炸波ꎮ
图 1 爆炸实验装置及实验现场布局图
Fig? 1 The explosive device used in experiments
依据外部钢壳的材料及厚度的差别ꎬ共开展四
个不同实验ꎬ实验装置的具体参数如表 1 所示ꎮ 所
有实验中钢柱壳的内径和长度均保持不变ꎬ因此ꎬ
TNT 当量均为 1 kgꎮ
表 1 爆炸装置相关参数列表
Table 1 The geometry parameters of the explosive devices
编 号 壳体材料 内径 r/ mm 外径 R/ mm 长度 L / mm 厚度 h / mm
1 Si ̄Mn 钢 25 30.5 240 5.5
2 Si ̄Mn 钢 25 33.5 240 8.5
3 45#钢 25 30.5 240 5.5
4 45#钢 25 33.5 240 8.5
实验在专门的爆炸场地开展ꎬ现场布局如图 1
所示ꎮ UHMWPE 复合板由背部的柔性沙袋支撑ꎬ表
面与装置的轴向平行ꎬ复合板中心距装置中心的距
离为 2 mꎮ 为收集破片的形状ꎬ在爆炸装置的下方
放置一沙箱ꎮ 同时沿爆炸装置表面处布置 PDV 激
光探针ꎬ用于获取爆炸后破片飞出时的速度ꎮ
3 实验结果
四个不同实验测试获取的装置外壳速度历程曲
线如图 2 所示ꎮ 曲线中的速度值随着时间连续变化
后出现中止ꎬ该处为外壳产生的破片撞击探针后导
致的探针损毁ꎬ本文中近似认为该速度为破片侵彻
复合板的入射速度值ꎮ 从曲线可以看出ꎬ速度曲线与
壳体的材料无关ꎬ只与外壳的厚度值相关ꎮ 对于较
厚的外壳(对应表 1 中 h = 8? 5 mm)ꎬ破片速度约为
1? 0 km/ sꎻ对于较薄的外壳(对应表 1 中 h = 5? 5 mm)ꎬ
破片速度约为 1? 3 km / sꎮ 此外ꎬ图 3 给出了实验中
回收的破片形貌及质量信息ꎮ 根据统计ꎬ对于较厚
的外壳装置ꎬ破片质量主要介于 2 g~9 g 之间ꎻ对于较
薄的外壳装置ꎬ破片质量主要介于 1 g~5 g 之间ꎮ
图 2 爆炸装置外壳测速曲线
Fig? 2 The velocity history of the shell checked by PDV probes
2021 年第 12 期 61
???????????????????????????????????????????????
破片和爆炸波联合加载下 UHMWPE 纤维复合材料失效行为实验研究
图 3 实验回收的外壳破片及其质量分布信息
Fig? 3 Typical morphology and mass of the collected fragments
如前所述ꎬ本文的主要目的是观察 UHMWPE
复合板在破片和爆炸波加载下的变形失效行为ꎬ因
此ꎬ后续将重点展示复合板的主要变形及失效特征ꎮ
3? 1 整体变形特征
尽管实验中采用了四种不同的加载装置ꎬ但对
于四块 UHMWPE 复合板而言ꎬ均发生了显著的整
体变形ꎬ主要表现为由爆炸冲击波导致的大范围不
可逆弯曲以及高速破片引发的局部侵彻击穿ꎮ 图 4
展示了其中两块复合板的典型变形形貌ꎮ
图 4 破片和爆炸波联合加载下 UHMWPE
复合板变形形貌图
Fig? 4 The macroscopic deformation characteristics of the
laminate panel under the explosive loading
在图 4 中ꎬ用圆圈单独标出了破片侵彻的部位ꎬ
其中实线圆圈表示侵彻部位被完全贯穿ꎬ虚线圆圈
表示侵彻部位未被贯穿ꎮ 从图 4(a)及图 4(b)中两
块复合板正面和背面的侵彻点数量可以看出ꎬ各自
分别只有两个点和三个点被完全击穿ꎬ绝大多数侵
彻点未能贯穿复合板ꎬ即复合板实现了对绝大多数
破片的有效防护ꎬ展现出了良好的防护效能ꎮ 除局
部部位的侵彻外ꎬ复合板还存在因爆炸波加载导致
的整体弯曲变形ꎬ这种变形虽然并未导致复合板出
现破坏性的损伤ꎬ但这是复合板吸收爆炸冲击能量
的重要模式[1]
ꎮ 不管是侵彻点位的局部变形还是整
体的不可逆弯曲变形ꎬ都是 UHMWPE 复合板吸收
冲击能量的有效方式ꎮ
上述复合板整体的变形特点反映出 UHMWPE
复合板在破片和爆炸波联合作用下具有较好的吸能
防护特性ꎮ 为深入认识 UHMWPE 复合板在联合冲
击下的失效过程以帮助相关工程结构的设计ꎬ接下
来将进一步讨论复合板的详细失效模式ꎮ
3? 2 脱层与屈曲
从实验后复合板的变形情况可见ꎬ复合板层间
的脱层及屈曲现象非常显著ꎬ特别是在边缘区域ꎮ
图 5(a)中展示了相关细节ꎬ可以看到ꎬ在边界处ꎬ屈
曲和脱层二者总是伴随发生ꎮ 此外ꎬ通过图 5(b)中
复合板背部的侵彻点处变形可以发现在侵彻点周围
也伴随着大量的屈曲变形发生ꎮ 进一步从侵彻点的
形貌特点可以看出ꎬ此处的屈曲也伴随着复合板层
间的脱层发生ꎮ 另一个重要现象是ꎬ复合板层间脱
62 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
层主要集中于靠近背部的区域ꎬ该现象主要由冲击
带来的压缩应力在背板自由表面处产生反射拉伸应
力而引起ꎬ因此脱层主要集中于靠近背板的区域ꎮ
对于破片和爆炸波二者的加载ꎬ都能在复合板内部
产生压缩应力进而在边缘处产生反射拉应力ꎬ因此ꎬ
两种加载都会导致复合板层间脱层的出现ꎮ
图 5 复合板边界处的脱层和屈曲(a)ꎬ
以及背部侵彻点周围的屈曲现象(b)
Fig? 5 The delamination and buckling at the boundary
of the panel (a)ꎬ and the buckling appearing at the
penetration sites of the rear face (b)
从能量吸收的角度ꎬ脱层和屈曲对于复合板防护
性能的发挥都是有益的ꎬ都能吸收冲击能量ꎮ 但是ꎬ
该两种失效模式都会影响复合板的抗侵彻性能ꎮ 如
图 6 所示ꎬ侵彻穿孔部位的细节形貌反映出复合板
内部的亚层结构及纤维并未按照最有利于其抗侵彻
性能发挥的模式发生变形及失效ꎮ 基于相关研究ꎬ
复合板内部亚层结构间相互膨胀挤压引起的间接拉
伸模式是 UHMWPE 复合板抗侵彻的基础ꎬ而复合
板层间的良好紧密黏结是保证间接拉伸模式出现的
必要条件[4]
ꎮ 因此ꎬ爆炸波诱发的层间脱层在一定
程度上导致复合板难以发挥其在抗侵彻上的优势ꎮ
图 6 边界脱层区域处的侵彻穿孔典型形貌
Fig? 6 The typical morphologies of the penetration holes
in the boundary delamination regions
3? 3 侵彻穿孔及鼓包
本部分主要分析讨论侵彻部位的穿孔及鼓包现
象ꎮ 不同复合板背部的形貌如图 7 所示ꎮ 对于破片
完全击穿复合板的位置ꎬ在侵彻孔周边具有非常明
显的面外凸起变形ꎻ对于未完全击穿的区域ꎬ侵彻导
致了明显的鼓包ꎬ鼓包的最大挠度值接近两倍复合
板厚度ꎬ这表明 UHMWPE 复合板具有良好的韧性ꎮ
此外ꎬ从图 7(c)和图 7(d)可以看到ꎬ部分未击穿区
域的鼓包与击穿孔非常靠近ꎬ这表明 UHMWPE 复
合板局部的侵彻贯穿失效不会降低相邻区域的侵彻
防护能力ꎬ该特点利于其对多破片侵彻的防护ꎮ
进一步地ꎬ图 7(e)和图 7(f)展示了鼓包及穿孔
部位的截面图ꎮ 在图 7(e)中ꎬ复合板成功阻止了破
片的侵彻ꎬ破片下方产生的面外大挠度变形以及层
间的良好黏结保证了 UHMWPE 能发挥出其基于间
接拉伸的良好抗侵彻性能ꎬ进而纤维的高拉伸强度
能发挥其在破片侵彻防护上的功效ꎮ 相反地ꎬ从图
7(f)中的侵彻孔截面并未看到明显的面外挠度变
形ꎬ该变形特点阻止了纤维发挥其预期的侵彻防护
效能ꎬ进而破片较为轻松地穿透了复合板ꎮ
图 7 复合板背部侵彻穿孔区域的典型形貌
(a)、(b)、(c)、(d)以及侵彻穿孔部位的截面图(e)、(f)
Fig? 7 The typical morphologies of the perforation and bubble
in the rear face (a)ꎬ (b)ꎬ (c) and (d)ꎬ and the sectional
views of the penetration holes (e) and (f)
3? 4 高温烧蚀
相比于传统的弹道实验ꎬ本文实验加载的重要特
征之一是破片在爆炸波加载下呈现出明显的高温特
性ꎬ即破片在侵彻复合板之前已被爆炸过程加热至
较高温度ꎮ 通常情况下ꎬ爆炸过程诱导的破片温度
高达数百摄氏度ꎮ 相关研究表明 UHMWPE 纤维对
温度较为敏感ꎬ因此ꎬ纤维在高温破片作用下出现的
烧蚀效应不可忽略ꎮ 图 8 展示了图 7( e)中侵彻孔
部位的 SEM 图像ꎮ 可以明显发现ꎬ大多数纤维出现
了烧蚀断裂的特征ꎬ进而导致其直接失去了抗侵彻
能力ꎮ 需要指出的是ꎬ烧蚀失效通常发生在破片侵
彻的初始阶段ꎬ随着侵彻过程的深入ꎬ破片温度逐渐
降低ꎬ高温烧蚀将不再是主要的失效模式ꎮ
2021 年第 12 期 63
???????????????????????????????????????????????
破片和爆炸波联合加载下 UHMWPE 纤维复合材料失效行为实验研究
图 8 侵彻区域内部对应图 7(e)侵彻孔的 SEM 图像
Fig? 8 The SEM photographs of the penetration
regions in Fig.7 (e)
4 分析与讨论
基于上述提到的主要变形特征和失效模式ꎬ可
分析获取 UHMWPE 复合板在破片和爆炸波联合加
载下的失效过程ꎮ 整体上讲ꎬUHMWPE 复合板的失
效过程可分为四个主要阶段ꎬ如图 9 所示ꎮ
图 9 UHMWPE 复合板在联合冲击加载下的失效过程
Fig? 9 The failure progress of the UHMWPE
panel under the explosive loading
在初始阶段ꎬ如图 9( a)所示ꎬ由破片和爆炸波
冲击复合板带来的压缩应力沿厚度方向传播ꎬ并且
该压缩应力波在到达复合板背部后反射变为拉伸应
力ꎮ 因此ꎬ拉应力导致的脱层失效将出现在靠近背
部的区域ꎬ特别是复合板的边缘处ꎮ 伴随着脱层的发
生ꎬ破片侵彻进入复合板内部ꎬ见图 9(b)ꎬ在破片进入
复合板的早期阶段ꎬ复合板来不及产生较为明显的
面外变形ꎬ高温高速破片诱发的纤维剪切及烧蚀断
裂成为该阶段的主要失效模式ꎮ 而随着破片侵彻深
度的增加ꎬ复合板在冲击作用下逐渐产生明显的面
外变形ꎬ此时失效模式开始发生变化ꎮ如图9(c)所示ꎬ
UHMWPE 纤维复合材料开始展现出最为典型的间
接拉伸失效模式ꎬ纤维的抗拉强度在侵彻防护中发
挥主导作用ꎮ 当间接拉伸产生的拉应力低于纤维的
拉伸强度时ꎬ破片侵彻过程被阻止ꎻ而当间接拉伸产
生的拉应力高于纤维的拉伸强度时ꎬ破片会继续向
前侵彻直至贯穿整个复合板ꎮ 在该过程中沿侵彻穿
孔区域周围出现明显的屈曲及脱层失效ꎬ见图 9(d)ꎮ
5 结 论
本文基于爆炸实验ꎬ系统观察了 UHMWPE 复合
板在破片和爆炸波联合作用下的变形行为及主要失
效模式ꎮ 结果表明ꎬUHMWPE 复合板在联合加载下
呈现复杂的失效模式ꎬ包括脱层、屈曲、鼓包、穿孔以
及纤维烧蚀断裂等ꎮ 联合加载下ꎬ复合板的失效过程
可分为四个主要阶段ꎮ 初始阶段ꎬ破片和爆炸波冲击
带来的压缩应力波在复合板背部发生反射拉伸造成
复合板靠近背部区域出现明显的脱层现象ꎻ当高温
破片开始侵彻进入复合板内部后ꎬ内部纤维的剪切
和烧蚀断裂成为主要失效模式ꎻ而随着侵彻过程的
进行ꎬ复合板逐渐产生较大的面外变形ꎬUHMWPE 纤
维复合材料开始展示出其特有的间接拉伸失效模式ꎬ
阻止破片侵彻ꎻ若破片能量足够高ꎬ其最终将穿透复
合板ꎬ此时穿孔周围将伴随明显的屈曲及脱层失效ꎮ
参考文献
[1] FALLAH A Sꎬ MICALLEF Kꎬ LANGDON G Sꎬ et al. Dynamic re ̄
sponse of dyneema HB26 plates to localised blast loading[J]. Inter ̄
national Journal of Impact Engineeringꎬ 2014ꎬ 73(1): 91 ̄100.
[2] CHOCRON Sꎬ KING Nꎬ BIGGER Rꎬ et al. Impacts and waves in
Dyneema
® HB80 strips and laminates[ J]. Journal of Applied Me ̄
chanicsꎬ 2013ꎬ 80(3): 472 ̄481.
[3] 张颖异ꎬ 李冰川ꎬ 刘发杰. PE ̄UHMW 抗弹复合材料及其在防护
领域中的应用[J]. 工程塑料应用ꎬ 2015ꎬ 43(10): 143 ̄146.
[4] O′MASTA M Rꎬ CRAYTON D Hꎬ DESHPANDE V Sꎬ et al. Mech ̄
anisms of penetration in polyethylene reinforced cross ̄ply laminates
[J]. International Journal of Impact Engineeringꎬ 2015ꎬ 86: 249 ̄264.
[5] 李翠玉ꎬ 杨雪ꎬ 冯亚男ꎬ 等. 不同层数的超高分子量聚乙烯纬平
针织复合材料冲击损伤[J]. 复合材料学报ꎬ 2015ꎬ32(2): 557 ̄564.
[6] 苏罗川ꎬ 宜晨虹ꎬ 刘文杰. 超高分子量聚乙烯纤维复合材料的应
用及其抗侵彻性能[J]. 化工新型材料ꎬ 2019ꎬ 47(1): 198 ̄201.
[7] GREENHALGH E Sꎬ BLOODWORTH V Mꎬ LIANNUCCIA Lꎬ et
al. Fractographic observations on Dyneema composites under ballistic
64 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
impact[J]. Composites Part A: Applied Science and Manufacturingꎬ
2013ꎬ 44: 51 ̄62.
[8] RUSSELL B Pꎬ KARTHIKEYAN Kꎬ DESHPANDE V Sꎬ et al. The
high strain rate response of ultra high molecular ̄weight polyethylene:
From fibre to laminate[J]. International Journal of Impact Engineer ̄
ingꎬ 2013ꎬ 60: 1 ̄9.
[9] ZHANG T Gꎬ SATAPATHY S Sꎬ VARGAS ̄GONZALEZ L Rꎬ et al.
Ballistic impact response of Ultra ̄High ̄Molecular ̄Weight Polyethylene
(UHMWPE)[J]. Composite Structuresꎬ 2015ꎬ 133: 191 ̄201.
[10] NGUYEN L Hꎬ RYAN Sꎬ CMPOERU S Jꎬ et al. The effect of target
thickness on the ballistic performance of ultra high molecular weight
polyethylene composite[J]. International Journal of Impact Engineer ̄
ingꎬ 2015ꎬ 75: 174 ̄183.
[11] ATTWOOD J Pꎬ RUSSELL B Pꎬ WADLEY H N Gꎬ et al. Mecha ̄
nisms of the penetration of ultra ̄high molecular weight polyethylene
composite beams[ J]. International Journal of Impact Engineeringꎬ
2016ꎬ 93: 153 ̄165.
[12] O′MASTA M Rꎬ COMPTON B Gꎬ GAMBLE E Aꎬ et al. Ballistic
impact response of an UHMWPE fiber reinforced laminate encasing
of an aluminum ̄alumina hybrid panel [ J]. International Journal of
Impact Engineeringꎬ 2015ꎬ 86: 131 ̄144.
[13] 李典ꎬ 侯海量ꎬ 朱锡ꎬ 等. 舰船装甲防护结构抗弹道冲击的研
究进展[J]. 中国造船ꎬ 2018ꎬ 59(1): 237 ̄250.
[14] 李典ꎬ 侯海量ꎬ 戴文喜ꎬ 等. 爆炸冲击波和破片联合作用下玻璃
纤维夹芯复合结构毁伤特性实验研究[J]. 兵工学报ꎬ 2017ꎬ 38
(5): 877 ̄885.
[15] ZHANG Rꎬ QIANG L Sꎬ HAN Bꎬ et al. Ballistic performance of
UHMWPE laminated plates and UHMWPE encapsulated aluminum
structures: Numerical simulation[J]. Composite Structuresꎬ 2020ꎬ
252: 112686.
(上接第 33 页)
6 结 论
可扁平输送软管的承压强度取决于织物增强层
的拉伸性能ꎬ而在纱线交叉点产生的应力集中会降
低织物的强度ꎮ 本文通过研究织物结构参数与纱线
交叉点处应力集中程度的关系ꎬ为优化织物增强层
结构ꎬ改善可扁平输送软管的承压性能提供了依据ꎮ
结果表明:斜纹环编织物有限元拉伸模拟结果和拉
伸试验结果基本相符ꎻ织物承受经向拉伸载荷时ꎬ经
纱间距、纬纱细度、纬纱卷曲率大小对交叉点处的应
力集中程度没有明显影响ꎻ织物承受纬向拉伸载荷
时ꎬ经纱间距增大、纬纱变细以及纬纱卷曲率降低可
以使纱线交叉点处的应力分布更加均匀ꎬ提高纱线
力学效率ꎬ纬纱卷曲率大于 4? 1%时ꎬ经纱间距、纬纱
细度以及纬纱卷曲率对交叉点处的应力集中程度影
响较大ꎮ
参考文献
[1] 谭凤旭ꎬ 杨立明. 高技术在外军油料补给装备上的应用[ J]. 现
代军事ꎬ 2000(7): 22 ̄23.
[2] 黄忠耀ꎬ 蔡利海ꎬ 蔡宝祥ꎬ 等. 一种多层筒形织物的设计方法:
2014104441910[P]. 2015 ̄01 ̄07.
[3] COIMBRA R Nꎬ OTERO M. A continuous process for the production
of a fabric reinforced polymeric matrix [ J]. Journal of Reinforced
Plastics and Compositesꎬ 2015ꎬ 34(20): 1662 ̄1672.
[4] 孙训方. 材料力学 ̄Ⅰ[M]. 北京: 高等教育出版社ꎬ 2009.
[5] 刘倩楠ꎬ 张涵ꎬ 刘新金ꎬ 等. 基于 ABAQUS 的三原组织机织物拉
伸力学性能模拟[J]. 纺织学报ꎬ 2019ꎬ 40(4): 44 ̄50.
[ 6] 李瑛慧ꎬ 谢春萍ꎬ 刘新金. 三原组织织物拉伸力学性能有限元仿
真[J]. 纺织学报ꎬ 2017ꎬ 38(11): 41 ̄47.
[7] CARVELLI Vꎬ CORAZZA Cꎬ POGGI C. Mechanical modelling of
monofilament technical textiles[J]. Computational Materials Scienceꎬ
2008ꎬ 42(4): 679 ̄691.
[8] SU Xꎬ LIU X. Dynamic tensile process of blended fabric using finite
element method [ J]. International Journal of Clothing Science and
Technologyꎬ 2020ꎬ 32(5): 707 ̄724.
[9] CHEN Sꎬ TIAN Xꎬ HUA Tꎬ et al. Exploring the relationship between
applied fabric strain and resultant local yarn strain within the elastic
fabric based on finite element method[ J]. Journal of Materials Sci ̄
enceꎬ 2020ꎬ 55(23): 10258 ̄10270.
[10] 赵书经. 纺织材料实验教程[M]. 北京: 中国纺织出版社ꎬ 1989.
[11] 顾平. 织物组织与结构学[M]. 上海: 东华大学出版社ꎬ 2010.
[12] 周炬. ANSYS Workbench 有限元分析实例详解: 静力学[ M].
北京: 人民邮电出版社ꎬ 2017.
[13] CARVELLI Vꎬ POGGI C. A homogenization procedure for the nu ̄
merical analysis of woven fabric composites[J]. Composites. Part Aꎬ
Applied Science and Manufacturingꎬ 2001ꎬ 32(10): 1425 ̄1432.
[14] DUAN Yꎬ KEEFE Mꎬ BOGETTI T Aꎬ et al. A numerical investiga ̄
tion of the influence of friction on energy absorption by a high ̄strength
fabric subjected to ballistic impact[J]. International Journal of Im ̄
pact Engineeringꎬ 2004ꎬ 32(8): 1299 ̄1312.
[15] 徐燕娜ꎬ 葛明桥. 夜光纤维摩擦与耐磨损性能研究[J]. 针织工
业ꎬ 2008(4): 17 ̄19.
[16] SHEN Yꎬ MEIR A Jꎬ CAO Y Zꎬ et al. Finite element analysis of
monofilament woven fabrics under uniaxial tension[J]. The Journal
of The Textile Instituteꎬ 2015ꎬ 106(1): 90 ̄100.
[17] FREDERICK T P. 5 ̄The geometry of cloth structure[J]. Journal of
the Textile Institute Transactionsꎬ 1937ꎬ 28(3): 45 ̄96.
2021 年第 12 期 65
???????????????????????????????????????????????
用于雷达天线的国产碳纤维预浸料成型工艺优化及配套材料优选
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 010
用于雷达天线的国产碳纤维预浸料成型工艺优化及配套材料优选
孙 坤1ꎬ2
ꎬ 赵文忠1ꎬ2
ꎬ 张晨晖1ꎬ2
ꎬ 刘明昌1ꎬ2
ꎬ 李建伟1ꎬ2
ꎬ 高 琦1ꎬ2
ꎬ 许培伦1ꎬ2
(1? 中国电子科技集团公司第二十研究所ꎬ 西安 710068ꎻ 2? 中电科西北集团有限公司ꎬ 西安 710068)
摘要: 为实现国产碳纤维/ 环氧树脂织物预浸料在雷达天线中的应用ꎬ开展以该碳纤维预浸料为蒙皮的夹层板热压罐成
型工艺流程和关键工艺参数优化研究ꎬ在此基础上ꎬ制备 6 种以碳纤维预浸料为蒙皮ꎬ分别以 J ̄95 或 SY ̄24C Ⅱ胶膜进行胶接ꎬ
填充 J ̄47D 或 SY ̄P6 发泡胶或不填充发泡胶的复合材料夹层板ꎬ通过平面拉伸、弯曲等力学性能测试分析对该预浸料用于夹
层板时的配套材料进行优选研究ꎮ 研究结果确定采用两步热压罐法进行不填充发泡胶和填充 J ̄47D 发泡胶的夹层板成型ꎬ采
用三步热压罐法进行填充 SY ̄P6 发泡胶的夹层板成型ꎬ并确定升/ 降温速率、加压时机等关键工艺参数和工装辅助等提高夹层
板质量的措施ꎻ对 6 种夹层板力学性能测试分析发现ꎬSY ̄24C Ⅱ胶膜与蒙皮、蜂窝以及发泡胶的匹配性更好ꎮ 而将两型发泡
胶相比ꎬ填充 SY ̄P6 发泡胶的夹层板的各项力学性能明显更优ꎬ因此优选 SY ̄24C Ⅱ胶膜和 SY ̄P6 发泡胶作为配套材料用于雷
达天线制造ꎮ
关键词: 碳纤维复合材料ꎻ 夹层板ꎻ 工艺优化ꎻ 配套材料ꎻ 力学性能
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0066-07
Optimization of forming process and supporting materials of
domestic carbon fiber prepreg for radar antenna
SUN Kun
1ꎬ2
ꎬ ZHAO Wen ̄zhong
1ꎬ2
ꎬ ZHANG Chen ̄hui
1ꎬ2
ꎬ LIU Ming ̄chang
1ꎬ2
ꎬ
LI Jian ̄wei
1ꎬ2
ꎬ GAO Qi
1ꎬ2
ꎬ XU Pei ̄lun
1ꎬ2
(1? The 20th Research Institute of China Electronics Technology Group Corporationꎬ Xi′an 710068ꎬ Chinaꎻ
2? China Electronics Technology Northwest Group Corporationꎬ Xi′an 710068ꎬ China)
Abstract:In order to realize the application of domestic developed carbon fiber/ epoxy resin fabric prepreg in
radar antennaꎬ the forming process and key process parameters optimization of sandwich plate autoclave with new ̄
developed carbon fiber prepreg as skin were studied. On this basisꎬ six kinds of composite sandwich panels were
prepared with newly prepared carbon fiber prepreg as skinꎬ bonded with J ̄95 or SY ̄24C Ⅱ filmꎬ filled with J ̄47D
or SY ̄P6 foam or not filled with foam. Through the test and analysis of plane tensile and bending mechanical proper ̄
tiesꎬ the supporting materials of the prepreg used in sandwich plate were optimized. The results of the study showed
that the two ̄step autoclave forming process was used to form the sandwich board without foam or the sandwich board
filled with J ̄47D foam and the three ̄step autoclave forming process was used to form the sandwich board filled with
SY ̄P6 foam. In additionꎬ the key process parametersꎬ such as the rate of heating or coolingꎬ the pressure timingꎬ
and the measures to improve the quality of sandwich panelꎬ such as tooling assistanceꎬ were determined. The me ̄
chanical properties of six kinds of sandwich panels were tested and analyzed. It was found that SY ̄24C Ⅱ film had a
better match with skinꎬ honeycomb and foamꎬ and compared with the two types of foamꎬ the mechanical properties
of the sandwich board filled with SY ̄P6 foam are obviously better. Thereforeꎬ SY ̄24C Ⅱ film and SY ̄P6 foam are
determined as supporting materials for the manufacture of radar antenna.
Key words:carbon fiber compositesꎻ sandwich panelsꎻ process optimizationꎻ supporting materialsꎻ mechanical
properties
收稿日期: 2021 ̄07 ̄05
基金项目: 国防科研项目 (TDXX ̄CL ̄19 ̄0XX ̄2)
作者简介: 孙坤 (1991 ̄)ꎬ 男ꎬ 硕士ꎬ 工程师ꎬ 主要从事复合材料方面的研究ꎬ MrSkain@163? comꎮ
66 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
碳纤维复合材料夹层板具有构件比重轻、比强度
和模量高、制品成型尺寸稳定性好、可设计性强、抗
疲劳性好、耐腐蚀性优异等优点ꎬ已被作为承力构件
广泛用于飞机、雷达、汽车、高铁等军民品领域[1 ̄3]
ꎮ
某雷达天线为通过热压罐成型方法制成的以碳纤维
复合材料预浸料为蒙皮、LF2Y 耐久铝蜂窝为芯材的
夹层结构ꎬ为满足天线装配和力学性能要求ꎬ通常还
需对夹层板边沿一定宽度填充发泡胶[4ꎬ5]
ꎮ
雷达天线成型过程涉及碳纤维复合材料与耐久
铝蜂窝、胶膜、发泡胶等多种不同特性材料的复合ꎬ
需在热压罐环境中历经多次加压、加热、降温、卸压
等ꎬ工艺过程复杂ꎬ在温度场梯度、固化交联反应、外
压等物理化学因素影响下容易产生热 ̄化学应变、残
余应力和固化变形等[6ꎬ7]
ꎮ 因此ꎬ雷达天线性能与
预浸料、胶膜等材料的特性以及成型工艺等密不可
分ꎬ材料匹配性不佳、工艺流程不合适或固化参数不
恰当ꎬ很难使夹层板性能达到最佳状态ꎬ甚至会引起
翘曲、鼓包ꎬ直接影响最终制件的性能[8 ̄10]
ꎮ
用于该雷达天线蒙皮的 AC319 / CF8010 预浸料
为国产中温固化碳纤维/ 环氧树脂织物预浸料ꎬ尚未
在工程实际中得到应用ꎬ没有可供参考的工程固化
工艺参数ꎬ缺乏发泡胶、胶膜等相关配套材料匹配性
研究技术积累ꎮ 为实现该预浸料在雷达天线中的应
用ꎬ需根据天线实际生产需求ꎬ结合该碳纤维预浸料
与胶膜、发泡胶等配套材料物化性能特点ꎬ开展夹层
板固化工艺流程和关键工艺参数工艺优化研究以及
配套材料优选研究ꎬ确定最佳固化工艺参数和适合
与该碳纤维预浸料配套使用的胶膜、发泡胶型号ꎮ
1 试验方案与方法
1? 1 主要原材料
AC319 / CF8010 碳纤维/ 环氧树脂织物预浸料:
含胶量为 36%ꎬ厚度为(0? 1±0? 01) mmꎬ面密度为
(100±1) g / m
2
ꎬ中国航空制造技术研究院ꎻLF2Y 耐
久铝蜂窝 EL ̄0? 05 ̄4W ̄5A02 ̄2800 ̄W1250 ̄T12ꎬ中航
西安飞机工业集团股份有限公司ꎻJ ̄95 胶膜ꎬ黑龙江
石化院ꎬSY ̄24C Ⅱ胶膜ꎬ中国航发北京航空材料研
究院ꎬ两种胶膜均为中温固化胶膜ꎬ厚度为(0? 20±
0? 02) mmꎻJ ̄47D 发泡胶ꎬ灰色片状ꎬSY ̄P6 发泡胶ꎬ
蓝色粉末状ꎬ两种发泡胶均由中国航发北京航空材
料研究院生产ꎮ
1? 2 试 验
1? 2? 1 工艺优化试验
针对天线使用需求ꎬ开展填充或不填充发泡胶
的夹层板固化工艺优化试验ꎬ根据预浸料等固化特
性参数ꎬ初步采用两步法成型夹层板ꎬ即先通过热压
罐成型两张蒙皮ꎬ再通过热压罐进行蒙皮与蜂窝芯
材的二次胶接[11]
ꎮ 单张蒙皮由 4 层预浸料铺贴而
成ꎬ固化温度和压力分别为 400 kPa、135 ℃ ꎬ保温
180 minꎬ蒙皮与蜂窝胶接温度和压力分别为 150 ℃、
135 ℃ꎬ保温 120 minꎮ
根据蒙皮是否翘曲、蒙皮与蜂窝胶接是否可靠、
夹层板是否有鼓包或凹陷等缺陷ꎬ针对性地进行成
型工艺优化ꎬ如加强升/ 降温速率和升/ 降压速率的
控制以及升/ 降温时间的选择等ꎻ同时ꎬ加强工艺过
程控制ꎬ采取工装、匀压板等措施确保夹层板外观质
量满足要求ꎮ
1? 2? 2 配套材料优选试验
初选 J ̄95 和 SY ̄24C Ⅱ胶膜及 J ̄47D、SY ̄P6 发
泡胶ꎬ按照工艺优化试验确定的夹层板成型工艺参
数和相关措施进行夹层板成型ꎬ采取先成型夹层板ꎬ
再机械加工测试样件的工艺流程ꎬ制备 6 种分别以
不同胶膜胶接、填充不同发泡胶或不填充发泡胶的
夹层板ꎬ通过对夹层板平面拉伸等力学性能测试分
析ꎬ对碳纤维复合材料与配套材料的匹配性进行优
选研究ꎬ夹层板尺寸为 600 mm×750 mmꎬ确保可裁
剪出各类性能测试样件ꎮ 配套材料优选试验方案如
表 1 所示ꎮ
表 1 碳纤维复合材料与配套材料优选试验方案
Table 1 Optimal test scheme of carbon fiber
composites and supporting materials
序 号 蒙 皮 芯 材 胶 膜 发泡胶 编 号
1
2
3
4
5
6
AC319 /
CF8010
LF2Y
铝蜂窝
J ̄95 无 J0
SY ̄24C Ⅱ 无 S0
J ̄95 J ̄47D JJ
J ̄95 SY ̄P6 JS
SY ̄24C Ⅱ J ̄47D SJ
SY ̄24C Ⅱ SY ̄P6 SS
1? 3 夹层板性能测试分析
通过平面拉伸、平面压缩、平面剪切、侧向压缩、
弯曲 5 项试验测试上述 6 种夹层板常温力学性能ꎬ平
面拉伸等 5 项试验依次按照 GB/ T 1452、GB/ T 1453、
GB/ T 1454、GB/ T 1455、GB/ T 1456 进行ꎬ试验在 SANS
CMT 5105 型电子万能试验机上进行ꎬ每种试样不少
于 5 件ꎮ 按照相关标准要求ꎬ机加工制备相应尺寸的
力学性能测试样件ꎮ 测试完成后根据相应标准依次
计算夹层结构抗平拉强度、芯子压缩强度、剪切强度、
2021 年第 12 期 67
???????????????????????????????????????????????
用于雷达天线的国产碳纤维预浸料成型工艺优化及配套材料优选
侧压强度、芯子剪切强度及夹层结构弯曲刚度ꎮ 通
过上述力学性能分析评估ꎬ确定最终优选匹配方案ꎮ
2 结果与讨论
2? 1 夹层板成型工艺优化
2? 1? 1 无填充发泡胶的夹层板
初步试验时出现夹层板翘曲、部分蒙皮与蜂窝
脱胶及夹层板边缘部分蜂格塌陷等问题ꎮ 非对称铺
层易产生应力不均ꎬ造成制件变形ꎬ为减少铺层带来
的变形[12ꎬ13]
ꎬ蒙皮按照“0°/ +45°/ -45°/ +90°” 方式
对称铺贴ꎻ为确保人工下料时纤维方向准确性和一
致性ꎬ下料时ꎬ采用定向限位下料工装辅助ꎮ 为保证
固化过程真空度符合设置要求ꎬ真空袋封装完进热
压罐前ꎬ必须通过关闭真空泵的保压测试来排除偶
然因素导致的真空袋“漏气” 现象ꎬ同时ꎬ真空度设
置为-98 kPaꎬ并采取先加压再升温和预固化的方式
确保蒙皮层间密实、无气泡ꎮ 蒙皮固化时采取零吸胶
工艺ꎬ保证蒙皮含胶量与前期摸底试验的一致[14]
ꎮ
为减少温度梯度和压力梯度引起的内应力ꎬ升/ 降温
速率分别降为 1 ℃ / min、-1 ℃ / minꎬ升/ 降压速率分
别减至 30 kPa / min、-50 kPa / minꎬ并采取阶梯式升/
降温方式ꎬ确保温度场的均匀性ꎮ 蒙皮固化工艺参
数设置如表 2 所示ꎮ
表 2 蒙皮固化时的固化工艺参数设置
Table 2 Setting of curing process parameters during skin curing
程序段
空气温度
/ ℃
模具温度
/ ℃
罐内压力
/ kPa
真空度
/ kPa
保温时间
/ min
1 45 25 400 -98 0
2 90 80 400 -98 0
3 82 80 400 -98 30
4 135 128 400 -98 0
5 135 130 400 -98 180
6 40 60 0 -98 0
针对夹层板的翘曲和部分蜂格塌陷等问题ꎬ对
蒙皮与蜂窝胶接时的真空度、升/ 降温速率、升/ 降压
速率等进行同步调整ꎬ同时ꎬ合理设计辅料铺贴方
式ꎬ如针对蒙皮表面光亮不利于粘接的问题ꎬ蒙皮固
化时ꎬ在预浸料表面依次铺贴隔离布和无孔膜ꎬ同步
实现蒙皮零吸胶和粗化ꎬ提高其可粘性ꎬ避免人工打
磨粗化的不均匀性ꎬ并采取工艺框辅助、匀压板均压
等措施避免蜂格塌陷ꎬ提高夹层板质量ꎮ
2? 1? 2 填充发泡胶的夹层板成型
初步采用两步法成型填充发泡胶的夹层板时ꎬ
发现填充 J ̄47D 发泡胶的夹层板表面平整ꎬ无鼓包
或凹坑ꎬ但发泡胶填充不够密实ꎬ蜂格内存在空洞ꎮ
这主要是由蜂格填充高度控制不当引起的ꎬ同时ꎬJ ̄
47D 呈片状ꎬ料粒尺寸分布宽ꎬ填充时部分尺寸较大
的料粒易发生“架桥”ꎮ 在后续填充时ꎬ采取机械粉
碎和过筛等方式控制料粒尺寸ꎻ发泡胶填充时ꎬ为确
保发泡胶恰好充实蜂格ꎬ料粒应填充至距蜂格上沿
2 mm~5 mmꎮ
两步法成型的填充 SY ̄P6 发泡胶的夹层板出现
大面积蒙皮鼓包ꎬ破坏蒙皮后发现鼓包处发泡胶未
充实蜂格ꎬ而未鼓包处蜂窝填充密实ꎬ破坏为蒙皮层
间剥离或发泡胶被拉断ꎬ详见图 1ꎮ 这可能是 SY ̄P6
固化过程中逸出的小分子气体被裹缚在蒙皮内或残
留在状胶料内的空气在蒙皮与蜂窝间的聚集造成
的ꎬ但通过加匀压板和延长抽真空时间等措施减少
真空袋内空气残留并不能解决蒙皮鼓包问题[15ꎬ16]
ꎮ
为此ꎬ采用先进行一侧蒙皮与蜂窝胶接(同时进行
SY ̄P6 的填充固化)ꎬ再进行另一层蒙皮与蜂窝胶接
的分步法进行夹层板复合ꎮ 但实际操作过程中发
现ꎬ在一侧蒙皮与蜂窝胶接后ꎬ蜂窝板仅单侧受力ꎬ
向无蒙皮一侧大幅收缩变形ꎬ严重翘曲ꎬ无法进行上
蒙皮的胶接固化ꎮ
图 1 鼓包夹层板及部分蒙皮破坏后外观图
Fig? 1 Appearance of bulge sandwich panel
and part of skin damaged
为解决上述问题ꎬ进一步优化填充 SY ̄P6 的夹
层板成型工艺ꎬ采取先固化蒙皮ꎬ并单独进行 SY ̄P6
的填充固化ꎬ然后进行蒙皮与已填充固化 SY ̄P6 的
蜂窝的胶接复合ꎮ 实践中为保证 SY ̄P6 固化后恰好
填平蜂格ꎬ胶料填充时ꎬ将铝蜂窝芯放置于平板模具
上ꎬ四周采用工艺框围挡ꎬ蜂格用胶料填平ꎬ并采用
匀压板确保压力均匀ꎮ SY ̄P6 固化后硬度高ꎬ为避
免残留在模具上的胶料打磨清理困难ꎬ同时增加发
泡胶与蒙皮胶接时的表面粗糙度ꎬ发泡胶填充时及
时清理蜂格以外发泡胶粉末ꎬ并在蜂窝两侧铺贴隔
68 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
离布ꎬ提高可粘性ꎮ 胶料发泡固化温度和压力分别
为 200 kPa、135 ℃ ꎬ保温 120 minꎻ真空度设置为-95
kPaꎬ升/ 降温速率分别设置为 2 ℃ / min、-2 ℃ / minꎬ
升/ 降压速率分别设置为 50 kPa / min、 - 100 kPa /
minꎮ 检查发现上述方法制备的夹层板蒙皮平整、无
鼓包、无凹陷ꎬ破坏蒙皮后发现发泡胶填充密实ꎬ破
坏为蒙皮层间剥离或发泡胶被拉断ꎬ同时ꎬ断面无
空洞ꎮ
基于上述工艺优化试验并兼顾生产效率和生产
成本ꎬ确定填充 J ̄47D 的夹层板和无填充的夹层板ꎬ
采用两步热压罐法成型ꎬ而填充 SY ̄P6 的夹层板采
用三步法成型ꎮ 相应力学性能测试样件制备工艺流
程如图 2、图 3 所示ꎮ
图 2 填充 J ̄47D 或无填充的夹层板成型工艺流程
Fig? 2 Forming process of sandwich plate filled
with J ̄47D or without filling
图 3 填充 SY ̄P6 的夹层板成型工艺流程
Fig? 3 Forming process of sandwich plate filled with SY ̄P6
2? 2 性能测试结果分析
2? 2? 1 平面拉伸性能测试及分析
平面拉伸试验主要考察试样的平拉强度和破坏
形式ꎬ胶接为弱连接ꎬ通过该测试可以分析评估两种
胶膜与碳纤维复合材料、铝蜂窝及发泡胶的匹配性ꎮ
不同夹层结构平面拉伸强度见图 4ꎬ部分试样平面
拉伸破坏情况如图 5 所示ꎬ根据结果可知ꎬJ0 试样蒙
皮与芯材部分脱胶ꎬ平拉强度为 1? 82 MPaꎬ且离散
系数过大(Cv
= 16? 47%)ꎬS0 试样以蜂窝局部破坏
为主ꎬ平拉强度为 3? 86 MPaꎬ表明 SY ̄24C Ⅱ胶膜与
纯铝蜂窝胶接的抗平拉性能更优ꎮ 填充 J ̄47D 的 JJ
和 SJ 试样均为蒙皮与蜂窝芯胶接处破坏ꎬ平拉强度
相差不大且与 S0 相近ꎻ填充 SY ̄P6 的 JS、SS 试样为
蒙皮分层破坏或芯层与蒙皮胶接面破坏ꎬ平拉强度
分别为 7? 56 MPa、8? 22 MPaꎬ说明 SY ̄P6 与 J ̄95、
SY ̄24C Ⅱ两型胶膜胶接时的抗平拉性能较 J ̄47D
的好ꎮ 分析可知:无论是否填充发泡胶ꎬSY ̄24C Ⅱ
胶接的试样抗平拉强度都更高ꎻ两型发泡胶相比ꎬ填
充 SY ̄P6 的试样平拉性能更高ꎮ
图 4 不同夹层结构试样平面拉伸强度
Fig? 4 Tensile strength of specimens with
different sandwich structures in plane
图 5 部分夹层结构平面拉伸试验破坏试样
Fig? 5 Failure specimens of some sandwich
structures in plane tensile tests
2? 2? 2 平面压缩性能测试及分析
平面压缩试验主要考察夹层板平压载荷的承载
能力ꎬ据此可分析两型发泡胶性能的优劣ꎮ 不同夹
层结构平面压缩强度见图 6ꎬ部分试样平面压缩破
坏情况见图 7ꎬ由图可知ꎬJ0、S0 试样均为铝蜂窝坍
塌破坏ꎬ平压强度基本一致ꎬ分别为 2? 21 MPa 和 2? 33
MPaꎮ 填充发泡胶后平压载荷由发泡胶和蜂窝壁同
时承载ꎬ且 J ̄47D、SY ̄P6 均为环氧类ꎬ发泡后自身强
度较高ꎬ能快速吸收能量和分散压力ꎬ因此抗平压强
度显著增加ꎮ 填充 J ̄47D 的 JJ、SJ 试样平压强度分
别为 7? 01 MPa 和 5? 87 MPaꎬ较未填充的提高 2 倍以
上ꎬ分析认为两种试样强度的差异与采用 J ̄47D 填
充时微孔的随机性有关ꎻ填充 SY ̄P6 的 JS、SS 试样
2021 年第 12 期 69
???????????????????????????????????????????????
用于雷达天线的国产碳纤维预浸料成型工艺优化及配套材料优选
的平压强度相当ꎬ分别为 33? 01 MPa 和 33? 44 MPaꎬ
比填充 J ̄47D 的提高 4 倍以上ꎬ这与料粒尺寸有关ꎬ
J ̄47D 填充时虽已机械粉碎ꎬ但其尺寸远大于粉状
SY ̄P6ꎬ固化后微孔的存在使其抗压强度较后者低ꎮ
根据上述分析可知ꎬ两种胶膜的夹层板抗平压性能
无明显差异ꎬ但两型发泡胶相比ꎬ填充 SY ̄P6 的试样
具有更强的抗平压性能ꎮ
图 6 不同夹层结构试样平面压缩强度
Fig? 6 Plane compressive strength of samples
with different sandwich structures
图 7 部分夹层板平面压缩试验破坏试样
Fig? 7 Failure samples of some sandwich panels
in plane compression test
2? 2? 3 平面剪切性能测试及分析
平面剪切试验主要考察夹层结构的平面剪切强
度和破坏形式ꎬ据此可评估两种胶膜与碳纤维复合
材料、铝蜂窝及发泡胶的匹配性ꎮ 不同夹层结构平
面剪切强度见图 8ꎬ部分试样平面剪切破坏情况如
图 9 所示ꎬJ0 或 S0 试样破坏发生在胶接面ꎬ胶接强度
分别为 0? 92 MPa、0? 97 MPaꎬ表明两种胶膜与纯铝
蜂窝胶接时的抗平面剪切强度较小且相差不大ꎮ 填
充 J ̄47D 发泡胶的 JJ、SJ 试样均为芯层与蒙皮胶接
处的发泡胶被剪切剥离ꎬ平面剪切强度分别为 2? 99
MPa、2? 65 MPaꎬ比纯铝蜂窝芯子提高 2 倍以上ꎻ填
充 SY ̄P6 的 JS、SS 试样主要为芯层和蒙皮胶接处破
坏、蒙皮剪切破坏等ꎬ剪切强度分别达到 4? 65 MPa
和 4? 51 MPaꎬ比纯铝蜂窝芯的平面剪切强度提高了
3 倍以上ꎬ填充发泡胶后抗剪强度的大幅提高与发泡
胶可以更有效地传递和分散剪切应力ꎬ有效防止蜂
窝壁过早剪切失稳有关ꎮ 根据上述可知ꎬ不填充或
填充 SY ̄P6 时ꎬ两种胶膜胶接的夹层板的抗平面剪
切性能无明显差异(平面剪切强度相差接近 5%)ꎬ
但填充 J ̄47D 时ꎬ采用 J ̄95 的夹层板平面剪切性能
更优ꎻ两种发泡胶对试样抗平面剪切性能影响与平
面拉伸试验结果一致ꎬ填充 SY ̄P6 的试样平面剪切
性能更高ꎮ
图 8 不同夹层结构试样平面剪切强度
Fig? 8 Plane shear strength of samples with
different sandwich structures
图 9 部分夹层板平面剪切试验破坏试样
Fig? 9 Failure samples of partial sandwich plates
in plane shear test
70 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
2? 2? 4 侧向压缩性能测试及分析
侧向压缩试验主要考察夹层结构抗侧向压缩载
荷的能力ꎬ据此可分析碳纤维复合材料蒙皮/ 铝蜂窝
与胶膜、发泡胶的匹配性ꎮ 不同夹层结构侧向压缩
强度见图 10ꎬSJ 试样侧向压缩破坏情况见图 11ꎬ侧
向加载条件下ꎬJ0、S0 试样载荷主要由两侧蒙皮承
载ꎬ试样均为端部蒙皮压缩破坏ꎬ侧压强度分别为
12? 34 MPa、14? 40 MPaꎮ 填充发泡胶后ꎬ发泡胶可以
分担和传递侧压载荷ꎬ夹层板侧压强度明显提高ꎮ
填充 J ̄47D 的 JJ、SJ 侧压强度分别为 25? 20 MPa、
25? 52 MPaꎬ较未填充的提高 2 倍以上ꎬ填充 SY ̄P6
发泡胶的 JS、SS 侧压强度分别为 34? 86 MPa、36? 65
MPaꎬ较填充 J ̄47D 的提高 50%左右ꎬ分析认为两种
发泡胶填充的试样的侧压强度的差异也与 J ̄47D 料
粒尺寸较大有关ꎮ 分析可知ꎬ两种胶膜相比ꎬSY ̄24C
Ⅱ胶接的夹层板抗侧压性能更好ꎬ两型发泡胶相比ꎬ
SY ̄P6 填充的夹层板抗侧向压缩性能更优ꎮ
图 10 六种不同夹层结构试样侧压强度
Fig? 10 Side compressive strength of samples with
different sandwich structures
图 11 SJ 夹层板侧向压缩试验破坏试样
Fig? 11 Specimens in lateral compression test of SJ sandwich plate
2? 2? 5 弯曲性能测试及分析
弯曲试验主要通过分析芯材剪切强度、夹层板
弯曲刚度ꎬ对碳纤维复合材料蒙皮、铝蜂窝与胶膜和
发泡胶的匹配性进行进一步评估ꎮ 不同夹层结构芯
材剪切强度、夹层板弯曲刚度分别见图 12、图 13ꎬ部
分试样弯曲破坏情况见图 14ꎬJ0、S0 均在弯曲载荷
加载处出现屈服变形ꎬ两种夹层板芯材的剪切强度
分别为 0? 87 MPa、0? 95 MPaꎬ弯曲刚度分别为 1? 33×
10
5
kN?mm
2
、1? 27×10
5
kN?mm
2
ꎮ 填充发泡胶后ꎬ复
合材料蒙皮、蜂窝芯和发泡胶共同承担弯曲载荷ꎬ芯
材剪切强度增加ꎬ因此ꎬ夹层结构抗剪切能力显著增
强ꎬ填充 J ̄47D 的 JJ、SJ 试样剪切强度分别为 3? 23
MPa、3? 21 MPaꎬ较未填充的提高近 4 倍ꎻ填充 SY ̄
P6 的 JS、SS 试样多在载荷加载处发生破坏ꎬ芯材剪
切强度均为 3? 83 MPaꎬ较未填充的提高 4 倍以上ꎮ
弯曲刚度主要用以评价夹层板抵抗弯曲变形的能
力ꎬ填充发泡胶后ꎬ整体抗弯曲变形能力增强ꎬ所以
试样弯曲刚度增加ꎬ填充 J ̄47D 的 JJ、SJ 试样弯曲刚
度分别为 1? 32×10
5
kN?mm
2
、1? 48×10
5
kN?mm
2
ꎻ填
充 SY ̄P6 的 JS、SS 试样弯曲刚度分别为 1? 85×10
5
kN?mm
2
、1? 69×10
5
kN?mm
2
ꎮ 分析可知ꎬ无填充或
填充 SY ̄P6 发泡胶时ꎬ采用不同种胶膜胶接的夹层
结构抗剪切性能和抗弯曲性能无明显差异ꎻ而填充
J ̄47D 发泡胶时ꎬSY ̄24C Ⅱ型胶接的夹层板抗弯曲
变形能力略强ꎬ但两种胶膜对芯材抗剪切性能无明
显影响ꎻ而胶膜相同时ꎬSY ̄P6 发泡胶填充的夹层板
抗剪切性能和抗弯曲变形性能更优ꎮ
图 12 六种不同夹层结构试样蜂窝芯材剪切强度
Fig? 12 Shear strength of honeycomb core material of
samples with different sandwich structures
图 13 六种不同夹层结构试样弯曲刚度
Fig? 13 Bending stiffness of specimens of
different sandwich structures
2021 年第 12 期 71
???????????????????????????????????????????????
用于雷达天线的国产碳纤维预浸料成型工艺优化及配套材料优选
图 14 部分夹层板弯曲试验破坏试样
Fig? 14 Failure samples of some sandwich plates in bending test
综合上述分析发现ꎬ只在填充 J ̄47D 时ꎬ采用 J ̄95
胶接的夹层板的平面剪切性能相对较好ꎬ其余情况
下ꎬSY ̄24C Ⅱ胶接的夹层板综合性能更为优异ꎬ表
明 SY ̄24C Ⅱ胶膜与蒙皮、蜂窝以及 SY ̄P6 发泡胶
的匹配性更好ꎮ 而两型发泡胶相比ꎬSY ̄P6 使用方
便ꎬ填充 SY ̄P6 发泡胶夹层板的平拉强度、平面压缩
强度等性能均明显优于 J ̄47Dꎮ
3 结 论
本文通过对国产碳纤维/ 环氧树脂织物预浸料
开展夹层结构成型工艺优化及配套材料优选研究ꎬ
得到如下结论:
(1)通过开展不填充和填充发泡胶的夹层板固
化工艺优化研究ꎬ确定了采用两步热压罐法进行不
填充发泡胶和填充 J ̄47D 发泡胶的夹层板成型ꎬ采
用三步热压罐成型法进行填充 SY ̄P6 发泡胶的夹层
板成型ꎬ优化了升/ 降温速率、升/ 降压速率、加压时
机、真空度等关键工艺参数ꎬ确定了工装辅助、辅料
铺贴、精细化控制等确保夹层板质量一致性的工艺
措施ꎮ
(2)通过对 J0、JJ 等 6 种夹层结构的五项力学性
能测试和综合分析ꎬ发现 SY ̄24C Ⅱ胶接的夹层板综
合性能更为优异ꎬ表明其与蒙皮、蜂窝以及发泡胶的
匹配性更好ꎻ而将两型发泡胶相比ꎬ填充 SY ̄P6 发泡
胶的夹层板的各项力学性能明显更优ꎬ因此优选
SY ̄24C Ⅱ胶膜和 SY ̄P6 发泡胶作为配套材料用于
雷达天线制造ꎮ
参考文献
[1] 徐樑华. 高性能 PAN 基碳纤维国产化进展及发展趋势[J]. 中国
材料进展ꎬ 2012ꎬ 31(10): 7 ̄13.
[2] 朱苗ꎬ 刘刚ꎬ 党婧. 尾翼盒段主承力结构用高温固化碳纤维复合
材料性能应用研究[J]. 宇航材料工艺ꎬ 2019ꎬ 49(2): 82 ̄85.
[3] 徐林ꎬ 王树浩ꎬ 蔡东旭ꎬ 等. 低密度碳纤维复合材料耐高温抗氧
化技术研究[J]. 稀有金属材料与工程ꎬ 2019ꎬ 48(11): 260 ̄267.
[4] 王伟ꎬ 左小彪ꎬ 冯志海ꎬ 等. 一种玻纤/ 环氧 ̄Nomex 蜂窝夹层复
合材料制备工艺与性能研究[J]. 玻璃钢/ 复合材料ꎬ 2015(10):
42 ̄46.
[5] 李莺歌ꎬ 关鑫ꎬ 陈维强ꎬ 等. 蜂窝夹层结构及其埋件的力学性能
研究[J]. 宇航材料工艺ꎬ 2018(4): 41 ̄45.
[6] 梁恒亮ꎬ 邱海鹏ꎬ 陈静ꎬ 等. 铝蜂窝夹层板正交结构件的制造方
法[J]. 航空制造技术ꎬ 2009(s1): 30 ̄32.
[7] 吴利华ꎬ 张婷. 复合材料热压罐固化工艺研发试验设计与适航
验证[J]. 航空制造技术ꎬ 2018ꎬ 61(19): 88 ̄92ꎬ 97.
[8] 张铖ꎬ 梁宪珠ꎬ 王永贵ꎬ 等. 热压罐工艺环境对于先进复合材料
框架式成型模具温度场的影响[J]. 材料科学与工程学报ꎬ 2011
(4): 547 ̄553.
[9] 赵书婧. 复合材料热压罐固化变形及压实过程分析[D]. 哈尔
滨: 哈尔滨工业大学ꎬ 2011.
[10] 张广成ꎬ 张鸿鸣ꎬ 徐恒元ꎬ 等. 碳纤维/ 环氧树脂超薄预浸料成
型工艺及胶膜匹配性研究[J]. 航空制造技术ꎬ 2018ꎬ 61(14):
38 ̄44.
[11] 袁超ꎬ 张明. 复合材料蜂窝夹层结构方向舵二次胶接成型技术
研究[J]. 科技与创新ꎬ 2019ꎬ 127(7): 98 ̄99.
[12] 陈蔚ꎬ 成理ꎬ 叶宏军ꎬ 等. Nomex 蜂窝夹层复合材料的成型工
艺研究[J]. 玻璃钢/ 复合材料ꎬ 2017(7): 70 ̄73.
[13] 李敏ꎬ 张宝艳. 不对称铺层复合材料变形规律的实验研究[ J].
玻璃钢/ 复合材料ꎬ 2006(5): 28 ̄31.
[14] 王东. 舱段用碳纤维/ 环氧树脂复合材料及其整体成型工艺
[D]. 哈尔滨: 哈尔滨工业大学ꎬ 2010.
[15] 于丽娟. 碳纤维/ 环氧树脂预浸料及其复合材料的成型工艺和
力学性能[D]. 上海: 东华大学ꎬ 2013.
[16] 汪亮ꎬ 孙玲. 变截面蜂窝夹层结构复合材料胶接工艺研究[ J].
玻璃钢/ 复合材料ꎬ 2009(3): 68 ̄70.
72 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 011
基于正交试验法的混杂纤维橡胶混凝土力学性能试验研究
朱鹏宇1
ꎬ 万后林2
ꎬ 朱 叶1
ꎬ 顾文虎1
(1? 淮阴工学院 建筑工程学院ꎬ 淮安 223000ꎻ 2? 江苏东辰建材有限公司ꎬ 淮安 223000)
摘要: 针对混杂纤维橡胶混凝土(HFRC)设计了正交试验ꎬ对其力学性能进行测试并与普通混凝土对比ꎬ分析了玄武岩
纤维体积率、聚丙烯纤维体积率和橡胶体积率对 HFRC 抗压、劈裂抗拉和抗折强度的影响ꎮ 结果表明:当玄武岩纤维体积率为
0? 3%、聚丙烯纤维体积率为 0? 2%、橡胶体积率为 5%时ꎬHFRC 各项性能表现最佳ꎮ 玄武岩纤维对 HFRCꎬ强度的影响程度最大ꎬ
掺入混杂纤维 HFRCꎬ强度有较大幅度提升ꎬ体现了良好的纤维“正混杂效应”ꎬ随着橡胶体积率增加ꎬHFRC 强度逐渐降低ꎮ 借
助 SEM 微观分析了纤维在 HFRC 中的桥接增强作用ꎬ对 HFRC 增韧阻裂机制进行了讨论ꎬ最后对 HFRC 强度进行了模型预测ꎮ
关键词: 混凝土ꎻ 力学性能ꎻ 玄武岩纤维ꎻ 聚丙烯纤维ꎻ 橡胶ꎻ 强度ꎻ SEM 微观分析ꎻ 复合材料
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0073-05
Experimental study on mechanical properties of hybrid fiber rubber
concrete based on orthogonal experiment
ZHU Peng ̄yu
1
ꎬ WAN Hou ̄lin
2
ꎬ ZHU Ye
1
ꎬ GU Wen ̄hu
1
(1? Faculty of Architecture and Civil Engineeringꎬ Huaiyin Institute of Technologyꎬ Huaian 223000ꎬ Chinaꎻ
2? Jiangsu Dongchen Building Materials Co.ꎬ Ltd.ꎬ Huaian 223000ꎬ China)
Abstract:Orthogonal experiments were designed for hybrid fiber rubber concrete (HFRC)ꎬ and its mechanical
properties were tested and compared with ordinary concrete. The volume ratio of basalt fiberꎬ polypropylene fiber
and rubber volume ratio were analyzed for the impact of HFRC′s compression and splitting strength. The results show
that when the volume ratio of basalt fiber is 0? 3%ꎬ the volume ratio of polypropylene fiber is 0? 2%ꎬ and the volume
ratio of rubber is 5%ꎬ the performance of HFRC is the best. Basalt fiber has an impact on the strength of HFRC and
the strength of HFRC mixed with hybrid fiber has been greatly improvedꎬ which reflects a good fiber " positive hy ̄
brid effect" . As the volume rate of rubber increasesꎬ the strength of HFRC gradually decreases. With the help of
SEM microscopic analysisꎬ the mechanism of fiber toughening and crack resistance of HFRC was discussedꎬ and fi ̄
nally the strength of HFRC was modeled.
Key words:concreteꎻ mechanical propertiesꎻ basalt fiberꎻ polypropylene fiberꎻ rubberꎻ strengthꎻ SEM micro ̄
analysisꎻ composites
收稿日期: 2021 ̄03 ̄01
基金项目: 江苏省自然科学基金 (BK20160426)
作者简介: 朱鹏宇 (1984 ̄)ꎬ 男ꎬ 实验师ꎬ 主要从事土木工程施工与管理方面的研究ꎬ zhu_huai@163? comꎮ
1 前 言
废轮胎的数量在全球范围内都在逐年增多ꎬ由
于废轮胎的成分较为复杂ꎬ其分解时间极为漫长ꎬ且
会对环境造成较大污染ꎮ 将废轮胎加工生产橡胶并
应用于混凝土中制备橡胶混凝土是废弃轮胎再生利
用的重要途径[1 ̄3]
ꎮ
橡胶混凝土与普通混凝土相比具有良好的抗冻
性、隔热性能和抗冲击性能等ꎬ但橡胶属于有机材
料ꎬ与水泥基体之间的黏结力较差ꎬ使得橡胶混凝土
基体的内部缺陷增多ꎬ力学性能相较于普通混凝土
有不同程度的下降[4 ̄6]
ꎮ 因此采取有效措施来提升
橡胶混凝土强度是众多专家学者的研究热点ꎬ研究
表明纤维混凝土能有效提高基体混凝土的强度[7 ̄10]
ꎮ
玄武岩纤维成本低廉、性能优良、绿色环保且具有较
高的弹性模量和极限应变ꎬ虽然聚丙烯纤维弹性模
量和极限应变低于玄武岩纤维ꎬ但断裂伸长率大于
玄武岩纤维[11 ̄14]
ꎮ 研究[15 ̄20] 表明:纤维在混凝土中
能起到阻止混凝土裂缝的产生和扩展的作用ꎬ能提
2021 年第 12 期 73
???????????????????????????????????????????????
基于正交试验法的混杂纤维橡胶混凝土力学性能试验研究
升混凝土的动态力学性能且对混凝土的强度有着较
好的提升ꎻ掺入聚丙烯纤维可显著改善混凝土的循
环受压力学行为ꎬ提高混凝土的抗冲击性能、峰后延
性、受压韧性及滞回耗能能力ꎬ降低混凝土的刚度退
化和应力劣化程度ꎮ
将玄武岩和聚丙烯纤维掺入橡胶混凝土中制备
HFRCꎬ以期两种纤维发生“正混杂效应”ꎬ提升橡胶
混凝土的力学性能ꎬ从而为相关工程实践提供理论
支撑ꎮ
2 试 验
2? 1 原材料
水泥:P?O 42? 5 级普通硅酸盐水泥ꎮ 粗骨料:
粒径为 5 mm~20 mm 的碎石ꎮ 细骨料:细度模数为
2? 75 的天然河砂ꎮ 橡胶:粒径为 1 mm ~ 3 mm 的橡
胶颗粒ꎬ密度为 1050 kg?m
-3
ꎮ 玄武岩纤维:短切玄
武岩纤维ꎮ 聚丙烯纤维:单丝束状聚丙烯纤维ꎮ 玄
武岩纤维和聚丙烯纤维的物理力学性能指标见表 1ꎮ
减水剂:HPWR 型高性能减水剂ꎬ减水率为 35%ꎮ 水:
自来水ꎮ
表 1 纤维部分性能参数
Table 1 Some performance parameters of fiber
纤 维
抗拉强度
/ MPa
弹性模量
/ GPa
密度
/ g?cm
-3
直径
/ μm
长度
/ mm
断裂伸长
率/ %
玄武岩纤维 3500 100 2.8 12 18 3.2
聚丙烯纤维 600 5.75 0.91 8 12 16
2? 2 试验设计
依据正交性采用正交试验法能在试验组数较多
时节省时间和成本ꎬ降低试验次数[21]
ꎮ 为研究玄武
岩纤维体积率(因素 A)、聚丙烯纤维体积率(因素
B)和橡胶体积率(因素 C)对 HFRC 抗压强度、劈裂
抗拉强度和抗折强度的影响规律ꎬ选用 L9(3
3
)正交
试验方案ꎬ每个因素各取三个水平ꎬ因素水平表见表
2ꎮ 根据 JGJ 55—2011 «普通混凝土配合比设计规
程»确定混凝土配合比设计ꎬ见表 3ꎮ
表 2 因素水平表
Table 2 Factor level table
水 平
玄武岩纤维体积率
(因素 A) / %
聚丙烯纤维体积率
(因素 B) / %
橡胶体积率
(因素 C) / %
1 0.1 0.1 5
2 0.2 0.2 10
3 0.3 0.3 15
表 3 混凝土配合比
Table 3 Concrete mix proportion (单位:kg?m
-3
)
试件
编号
水
泥
石
子
砂
子
玄武岩
纤维
聚丙烯
纤维
橡
胶
水
减水
剂
C 465 1245 600 0 0 0 155 5.15
H ̄1 465 1242 600 2.8 0.91 52.5 155 5.15
H ̄2 465 1242 600 2.8 1.82 105 155 5.15
H ̄3 465 1242 600 2.8 2.73 157.5 155 5.15
H ̄4 465 1242 600 5.6 0.91 105 155 5.15
H ̄5 465 1242 600 5.6 1.82 157.5 155 5.15
H ̄6 465 1242 600 5.6 2.73 52.5 155 5.15
H ̄7 465 1242 600 8.4 0.91 157.5 155 5.15
H ̄8 465 1242 600 8.4 1.82 52.5 155 5.15
H ̄9 465 1242 600 8.4 2.73 105 155 5.15
2? 3 试件制作及试验方法
试件制作时ꎬ首先将石子和砂子混合干拌 2
minꎬ然后倒入纤维和橡胶继续干拌 2 minꎬ接着加入
水泥再干拌 2 minꎬ最后加入水和减水剂搅拌 3 minꎬ
浇筑完成试件ꎮ 抗压强度和劈裂抗拉强度试验每组
各制作 3 个 100 mm×100 mm×100 mm 的立方体试件ꎬ
抗折强度每组制作 3 个 100 mm×100 mm×400 mm
的长条形试件ꎬ标准养护 28 dꎮ
试验方案参照 GB / T 50081—2002«普通混凝土
力学性能试验方法标准»进行ꎮ
3 试验结果与分析
3? 1 试验结果
基准混凝土和 HFRC 强度试验结果如表 4 所示ꎬ
基于表 4 中试验结果可以直观地看出 HFRC 的抗压
强度、劈裂抗拉强度和抗折强度均大于普通混凝土ꎬ
这表明玄武岩纤维、聚丙烯纤维和橡胶掺入混凝土
中有利于其力学性能的提升ꎻ同时对 HFRC 9 组试
验结果的直观分析可知ꎬH ̄8 组力学性能表现最佳ꎬ
即当玄武岩纤维体积率为 0? 3%、聚丙烯纤维体积率
为 0? 2%、橡胶体积率为 5%时ꎬ抗压强度、劈裂抗拉
强度和抗折强度达到峰值ꎬ分别为 48? 9 MPa、6? 73 MPa
和 9? 08 MPaꎻ另一方面相较于普通混凝土ꎬH ̄8 组三
种强度增幅分别为 42? 57%、46? 62%和 32? 75%ꎬ这
表明三因素对 HFRC 劈裂抗拉强度的影响最大ꎮ
74 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
表 4 各组试件抗压强度、劈裂抗拉强度和抗折强度试验结果
Table 4 Test results of compressive strengthꎬ splitting tensile
strength and flexural strength of each group
试件编号 抗压强度/ MPa 劈裂抗拉强度/ MPa 抗折强度/ MPa
C 34.3 4.59 6.84
H ̄1 38.9 5.35 7.7
H ̄2 39.2 5.31 7.66
H ̄3 35.5 4.82 7.15
H ̄4 43.8 6.29 8.64
H ̄5 43.5 5.75 8.1
H ̄6 44.2 5.68 8.03
H ̄7 45.3 6.06 8.41
H ̄8 48.9 6.73 9.08
H ̄9 47.8 6.34 8.69
3? 2 极差分析
对表 4 中 HFRC 抗压强度、劈裂抗拉强度和抗
折强度进行极差分析ꎬ结果如表 5 所示ꎬ绘制三因素
对 HFRC 抗压强度、劈裂抗拉强度和抗折强度影响
趋势ꎬ如图 1(a)至图 1(c)所示ꎮ
表 5 HFRC 强度极差分析结果
Table 5 HFRC strength range analysis results
抗压强度
因素
A
因素
B
因素
C
抗拉强度
因素
A
因素
B
因素
C
抗折强度
因素
A
因素
B
因素
C
K1 37.87 42.67 44 5.16 5.9 5.92 7.503 8.25 8.27
K2 43.83 43.87 43.6 5.907 5.93 5.98 8.257 8.28 8.33
K3 47.33 42.5 41.43 6.377 5.613 5.543 8.727 7.957 7.887
R 9.47 1.37 2.57 1.217 0.317 0.437 1.223 0.323 0.443
(a)
(b)
(c)
图 1 三因素对 HFRC 抗压强度、劈裂抗拉强度
和抗折强度影响趋势
Fig? 1 Influence trend of three factors on compressive strengthꎬ
splitting tensile strength and flexural strength of HFRC
由表 5 可知:三因素对 HFRC 抗压强度、劈裂抗
拉强度和抗折强度的影响大小均为玄武岩纤维体积
率>橡胶体积率>聚丙烯纤维体积率ꎮ
由图 1 可以看出:随着玄武岩纤维体积率的增加ꎬ
HFRC 的抗压强度、劈裂抗拉强度和抗折强度均逐
渐增大ꎬ当玄武岩纤维体积率从 0? 1%增加到 0? 3%时ꎬ
HFRC 抗压强度、劈裂抗拉强度和抗折强度增幅分别
为 25? 85%、23? 59%和 16? 31%ꎻ随着聚丙烯纤维体积
率的增加ꎬHFRC 的抗压强度、劈裂抗拉强度和抗折
强度均呈现先增大后降低的趋势ꎬ当聚丙烯纤维体积
率从0? 1%增加到0? 2%时ꎬHFRC 抗压强度、劈裂抗拉
强度和抗折强度增幅分别为 2? 81%、0? 51%和 0? 36%ꎬ
当聚丙烯纤维体积率从 0? 1%增加到 0? 3%时ꎬHFRC
三种强度分别降低 0? 4%、4? 86%和 3? 55%ꎻ随着橡
胶体积率的增加ꎬHFRC 抗压强度逐渐降低ꎬ劈裂抗
拉强度和抗折强度先上升后下降ꎬ当橡胶体积率从
5%增加到 10%时ꎬHFRC 劈裂抗拉强度和抗折强度
分别增长 1? 01%和 0? 73%ꎬ当橡胶体积率从 5%增
加到 15%时ꎬHFRC 抗压强度、劈裂抗拉强度和抗折
强度分别降低 5? 84%、6? 37%和 4? 63%ꎮ
2021 年第 12 期 75
???????????????????????????????????????????????
基于正交试验法的混杂纤维橡胶混凝土力学性能试验研究
3? 3 方差分析
表 6 给出了 HFRC 强度方差分析结果ꎮ
表 6 HFRC 方差计算结果
Table 6 Calculation results of HFRC variance
指 标 因 素 离散平方和 均 方 自由度 F 值 显著性
抗压强度
/ MPa
A 137.47 68.73 2 190.34 ∗∗
B 3.34 1.67 2 4.62 ?
C 11.44 5.72 2 15.84 ∗
E 0.72 0.36 2 - -
劈裂抗拉
强度/ MPa
A 2.26 1.13 2 27.71 ∗∗
B 0.18 0.09 2 1.76 △
C 0.34 0.17 2 3.23 ?
E 0.1 0.05 2 - -
抗折强度
/ MPa
A 2.28 1.14 2 23.12 ∗∗
B 0.19 0.1 2 1.94 △
C 0.35 0.17 2 3.51 ?
E 0.1 0.05 2 - -
注:∗∗表示特别显著ꎻ∗表示显著ꎻ?表示有一定影响ꎻ△表示
非显著性因素ꎮ
基于表 6 中对 HFRC 抗压强度、劈裂抗拉强度
和抗折强度的方差分析可知:玄武岩纤维体积率是
影响 HFRC 三种强度的特别显著性因素ꎻ聚丙烯纤
维体积率对 HFRC 的抗压强度有一定影响ꎬ且聚丙
烯纤维是影响 HFRC 劈裂抗拉强度和抗折强度的非
显著性因素ꎻ橡胶体积率是影响 HFRC 抗压强度的
显著性因素ꎬ对 HFRC 劈裂抗拉强度和抗折强度的
影响较为接近ꎬ水平均表现为有一定影响ꎬ但对抗折
强度的影响大于对劈裂抗拉强度的影响ꎮ
3? 4 功效系数分析
对表 4 中 HFRC 抗压强度、劈裂抗拉强度和抗
折强度进行功效系数分析ꎬ结果如表 7 所示ꎮ
表 7 HFRC 功效系数分析结果
Table 7 Analysis results of HFRC efficiency coefficient
编
号
指 标
抗压
强度
/ MPa
劈裂抗
拉强度
/ MPa
抗折
强度
/ MPa
功效系数
抗压
强度
d1
劈裂抗
拉强度
d2
抗折
强度
d3
总功
效系
数值
H ̄1 38.9 5.35 7.7 70.15 71.1 71.4 70.88
H ̄2 39.2 5.31 7.66 71.04 70.26 70.57 70.62
H ̄3 35.5 4.82 7.15 60 60 60 60
H ̄4 43.8 6.29 8.64 84.78 90.79 90.88 88.77
H ̄5 43.5 5.75 8.1 83.88 79.48 79.69 80.99
H ̄6 44.2 5.68 8.03 85.97 78.01 78.24 80.66
H ̄7 45.3 6.06 8.41 89.25 85.97 86.11 87.1
H ̄8 48.9 6.73 9.08 100 100 100 100
H ̄9 47.8 6.34 8.69 95.72 91.83 91.92 93.14
根据表 7 中总功效系数值的对比可知ꎬH ̄8 组
试件总功效系数最大ꎬ为 100ꎬ因此ꎬ综合抗压强度、
劈裂抗拉强度和抗折强度三种指标最佳配合比组合
为 A3B2C1 ꎬ即玄武岩纤维体积率为 0? 3%ꎬ聚丙烯纤
维体积率为 0? 2%ꎬ橡胶体积率为 5%ꎮ
3? 5 力学性能影响因素分析
混凝土在承受外部荷载初始阶段的应力主要是
由 HFRC 基体承担的ꎬ此时应力较小ꎬ随着加荷的继
续ꎬ试件内部产生微裂缝并慢慢发展成贯穿整个试
件的裂缝ꎬ此时高弹性模量的玄武岩纤维通过与混
凝土基体之间的机械咬合力和黏结力来承担主要的
荷载ꎬ发挥着玄武岩纤维的增强作用ꎮ 随着荷载的
继续增加ꎬ当小裂缝发展成为较大的裂缝时ꎬ玄武岩
纤维与混凝土基体之间的桥接作用形成的黏结力会
变小很多ꎬ此时聚丙烯纤维经过受压变形之后开始
与玄武岩纤维共同作用ꎬ协同增强了混凝土基体的
强度ꎬ体现了纤维的“正混杂效应”ꎬ但由于聚丙烯
纤维的弹性模量较低ꎬ对混凝土的增强作用有限ꎬ所
以相较于玄武岩纤维增强作用要小很多ꎮ
橡胶掺入混凝土中能够改善 HFRC 的和易性ꎬ
但从前文对 HFRC 三种强度的极差分析和方差分析
可以看出:一方面ꎬ橡胶不是影响 HFRC 强度的显著
性因素ꎬ另一方面ꎬ一定量的橡胶掺入混凝土中对混
凝土强度有着一定程度的提升ꎬ但效果并不明显ꎬ且
超过该掺量之后混凝土强度出现负增长ꎮ
4 SEM 微观分析
由图 2 可以看出ꎬ裸露在外的纤维表面覆盖有
稠密的刺状或球状物质ꎬ这些物质主要是水泥水化
基质(C ̄S ̄H 凝胶)ꎬ在 HFRC 水化反应过程中ꎬC ̄S ̄
H 凝胶与水泥二次水化产物钙矾石紧密包裹着纤
维ꎬ当纤维受拉时ꎬ可以与水泥基质形成一定的机械
咬合力ꎬ因此分散在 HFRC 内部的单根纤维作用与
钢筋类似ꎬ纤维与混凝土基体的紧密结合起到了二
次微加筋的作用ꎬ同时纤维交互形成的三维网状结
构以及纤维的桥接作用加强了纤维与基体的黏结ꎬ
有效地提升了 HFRC 的力学性能ꎮ
图 2 纤维与基体的黏结
Fig? 2 Bond between fiber and matrix
76 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
5 HFRC 强度预测模型
依据材料力学理论ꎬ假设 HFRC 强度由混凝土
基体强度、玄武岩纤维增强项、聚丙烯纤维增强项和
橡胶增强项共同组成ꎮ 假定强度回归模型为:
f =β0
+ β1
x1
+ β2
x2
+ β3
x3
+ α (1)
式中: f 为混凝土抗压强度、劈裂抗拉强度或抗折强
度ꎬMPaꎻβ0为混凝土基体抗压强度或劈裂抗拉强
度ꎬMPaꎻβ1 ꎬ β2 ꎬ β3为回归系数ꎻα 为试验参数ꎻx1为
玄武岩纤维体积率ꎬ%ꎻx2为聚丙烯纤维体积率ꎬ%ꎻ
x3为橡胶体积率ꎬ%ꎮ
将表 4 中数据代入回归模型(1)中ꎬ对 β 进行最
小二乘法估计得出 HFRC 抗压强度、劈裂抗拉强度
和抗折强度的回归方程为:
f
c
=36.28 + 4733x1
- 83x2
- 25.7x3(R
2 =0.94) (2)
f
t
=5.261 + 608x1
- 143x2
- 3.77x3(R
2 =0.89) (3)
f
f
=7.616 + 612x1
- 147x2
- 3.83x3(R
2 =0.89) (4)
式中: f
c 为 HFRC 抗压强度ꎬMPaꎻ f
t 为 HFRC 劈裂
抗拉强度ꎬMPaꎻf
f 为 HFRC 抗折强度ꎬMPaꎻR
2 为决
定系数ꎮ
6 结 论
(1)HFRC 抗压强度、劈裂抗拉强度和抗折强度
均大于普通混凝土ꎬ抗压强度为 35? 5 MPa ~48? 9 MPaꎬ
劈裂抗拉强度为 4? 82 MPa ~ 6? 73 MPaꎬ抗折强度为
7? 15 MPa~9? 08 MPaꎬ表明玄武岩和聚丙烯纤维及
橡胶有利于试件强度的提升ꎮ
(2)三因素对 HFRC 抗压强度、劈裂抗拉强度和
抗折强度的影响程度依次为玄武岩纤维体积率>橡
胶体积率>聚丙烯纤维体积率ꎬ当玄武岩纤维体积率
从 0? 1%增加到 0? 3%时ꎬHFRC 抗压强度、劈裂抗拉
强度和抗折强度分别增长 25? 85%、23? 59%和 16? 31%ꎮ
(3)玄武岩纤维体积率是影响 HFRC 强度的特别
显著性因素ꎻ聚丙烯纤维对 HFRC 抗压强度有一定
影响ꎬ且是 HFRC 劈裂抗拉强度和抗折强度的非显
著性因素ꎻ橡胶体积率是影响 HFRC 抗压强度的显
著性因素ꎬ且对 HFRC 劈裂抗拉强度和抗折强度有
一定影响ꎬ但对抗折强度的影响大于对劈裂抗拉强
度的影响ꎮ
(4)玄武岩纤维和聚丙烯纤维混杂能够表现出
较好的纤维协同作用增强 HFRC 的强度ꎬ体现了较
好的纤维“正混杂效应”ꎬ本文研究的 HFRC 中ꎬ当
橡胶体积率为 5%时ꎬ其对强度的提升有着一定的作
用ꎬ但超过 5%后ꎬHFRC 强度会呈现负增长效应ꎮ
(5)基于功效系数法进行分析ꎬ得出最佳组合为
A3B2C1 ꎬ即玄武岩纤维体积率为 0? 3%ꎬ聚丙烯纤维
体积率为 0? 2%ꎬ橡胶体积率为 5%ꎬ同时借助 SEM
微观分析了纤维在 HFRC 中的桥接增强作用ꎬ最后
对 HFRC 抗压强度、劈裂抗拉强度和抗折强度进行
了预测ꎮ
参考文献
[1] 邢君ꎬ 郭永伟ꎬ 张郁芳. 硅粉/ 废轮胎橡胶/ 混凝土复合材料的力
学性能和耐久性[J]. 合成橡胶工业ꎬ 2020ꎬ 43(5): 407 ̄413.
[2] 赵江霞ꎬ 高越青ꎬ 梁超锋ꎬ 等. 橡胶混凝土动态力学性能研究进
展[J]. 混凝土ꎬ 2020(8): 37 ̄40.
[3] 胡艳丽ꎬ 高培伟ꎬ 李富荣ꎬ 等. 不同取代率的橡胶混凝土力学性
能试验研究[J]. 建筑材料学报ꎬ 2020ꎬ 23(1): 85 ̄92.
[4] 陈疏桐ꎬ 陈建东ꎬ 薛旭. 玄武岩纤维橡胶混凝土力学及冻融性能
试验研究[J]. 混凝土与水泥制品ꎬ 2020(4): 54 ̄58.
[5] 白春ꎬ 麻凤海ꎬ 刘书贤ꎬ 等. 塑钢纤维增强橡胶混凝土耐硫酸盐
侵蚀试验[J]. 非金属矿ꎬ 2019ꎬ 42(3): 32 ̄35.
[6] 赵秋红ꎬ 董硕ꎬ 朱涵. 钢纤维 ̄橡胶/ 混凝土抗剪性能试验[J]. 复
合材料学报ꎬ 2020ꎬ 37(12): 3201 ̄3213.
[7] 韩嵘ꎬ 赵顺波ꎬ 曲福来. 钢纤维混凝土抗拉性能试验研究[ J].
土木工程学报ꎬ 2006(11): 63 ̄67.
[8] 寇佳亮ꎬ 赵坤龙ꎬ 张浩博. 高延性纤维混凝土拉压疲劳性能试验
研究[J]. 土木工程学报ꎬ 2018ꎬ 51(9): 17 ̄25.
[9] 张勇ꎬ 谢卫红ꎬ 刘宏伟ꎬ 等. 钢 ̄聚丙烯混杂纤维混凝土静态压
缩力学性能试验[J]. 混凝土ꎬ 2016(2): 66 ̄69ꎬ 73.
[10] 庞建勇ꎬ 张琴ꎬ 姚韦靖ꎬ 等. 钢纤维橡胶混凝土力学性能试验
[J]. 中国科技论文ꎬ 2020ꎬ 15(11): 1302 ̄1307.
[11] 朱华军. 玄武岩纤维混凝土耐久性能试验研究[D]. 武汉: 武
汉理工大学ꎬ 2009.
[12] 余春. 高性能聚丙烯纤维混凝土性能研究[D]. 重庆: 重庆交
通大学ꎬ 2009.
[13] 蹇守卫ꎬ 孔维ꎬ 马保国ꎬ 等. 纤维对薄层砂浆早期塑性收缩的
影响[J]. 材料导报ꎬ 2014ꎬ 28(22): 109 ̄113.
[14] 韩凯. 多尺度纤维增强水泥基材料的性能及机理研究[D]. 哈
尔滨: 哈尔滨工业大学ꎬ 2017.
[15] 王振山ꎬ 李浩炜ꎬ 吴波ꎬ 等. 玄武岩纤维混凝土的耐碱腐蚀性
及力学性能试验研究[J]. 应用力学学报ꎬ 2019ꎬ 36(5): 1088 ̄
1095ꎬ 1258 ̄1259.
[16] 朱涵ꎬ 刘昂ꎬ 于泳. 低温下玄武岩纤维混凝土的抗冲击性能
[J]. 材料科学与工程学报ꎬ 2018ꎬ 36(4): 600 ̄604.
[17] 杨智硕ꎬ 张晔芝ꎬ 叶梅新ꎬ 等. 超高强玄武岩纤维混凝土力学
性能研究[J]. 建筑科学ꎬ 2018ꎬ 34(11): 94 ̄98.
[18] 徐礼华ꎬ 黄彪ꎬ 李彪ꎬ 等. 循环荷载作用下聚丙烯纤维混凝土
受压应力 ̄应变关系研究[J]. 土木工程学报ꎬ 2019ꎬ 52(4): 1 ̄12.
[19] 刘新荣ꎬ 柯炜ꎬ 梁宁慧ꎬ 等. 基于 SHPB 试验的多尺寸聚丙烯
纤维混凝土动态力学性能研究[J]. 材料导报ꎬ 2018ꎬ 32( s1):
484 ̄489.
[20] 刘新荣ꎬ 柯炜ꎬ 梁宁慧ꎬ 等. 基于 SHPB 试验的多尺寸聚丙烯
纤维混凝土动态力学性能研究[J]. 材料导报ꎬ 2018ꎬ 32( s1):
484 ̄489.
[21] 方开泰ꎬ 马长兴. 正交与均匀试验设计[M]. 北京: 科学出版
社ꎬ 2001.
2021 年第 12 期 77
???????????????????????????????????????????????
复合材料水下防护结构在海洋油气开发的应用
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 012
复合材料水下防护结构在海洋油气开发的应用
石锦坤1
ꎬ 刘 辉3
ꎬ 张西伟2
ꎬ 郭 飞1∗
(1? 深圳海油工程水下技术有限公司ꎬ 深圳 518000ꎻ 2? 海洋石油工程股份有限公司安装事业部ꎬ 天津 300451ꎻ
3? 北京玻钢院复合材料有限公司ꎬ 北京 102101)
摘要: 随着海洋油气开发的快速发展ꎬ水下生产设施越来越多ꎬ与此同时ꎬ海洋渔业捕捞方式及捕捞设备发展迅速ꎬ渔业
活动对这些水下设施的影响也越发明显ꎬ被拖网、落锚损伤和破坏事故时有发生ꎮ 为了保证海上油气安全生产ꎬ需对水下设施
进行保护ꎮ 纤维增强复合材料具有重量轻、强度高、耐腐蚀、不易生长海生物等特点ꎬ在制作海洋油气开发水下设施防护结构
方面应用前景广阔ꎮ 本文主要对此类复合材料防护结构的应用情况进行概述ꎬ并与钢结构、水泥压块防护结构进行对比分析ꎮ
关键词: 海洋油气ꎻ 水下设施ꎻ 复合材料防护结构
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0078-05
Application of composite materials protector in the subsea of offshore oil
SHI Jin ̄kun
1
ꎬ LIU Hui
3
ꎬ ZHANG Xi ̄wei
2
ꎬ GUO Fei
1∗
(1? Shenzhen COOEC Subsea Technology Co.ꎬ Ltd.ꎬ Shenzhen 518000ꎬ Chinaꎻ
2? COOEC Offshore Divisionꎬ Tianjin 300451ꎬ Chinaꎻ
3? Beijing Composite Materials Co.ꎬ Ltd.ꎬ Beijing 102101ꎬ China)
Abstract:With the rapid development of offshore oil and gas developmentꎬ there are more and more underwater
production facilities. At the same timeꎬ marine fishery fishing methods and fishing equipment are developing rapidly.
The impact of fishing activities on these underwater facilities is becoming more and more obviousꎬ and they are dam ̄
aged by trawling and anchoring. And destruction accidents happen from time to time. In order to ensure the safe pro ̄
duction of offshore oil and gasꎬ underwater facilities need to be protected. Fiber ̄reinforced composite materials have
the advantages of light weightꎬ high strengthꎬ corrosion resistanceꎬ and difficulty in growing marine organisms.
Thereforeꎬ the application of protective structures for marine oil and gas development underwater facilities has broad
application prospects. This article mainly summarizes the application of this type of composite material protection
structureꎬ and compares and analyzes it with steel structure and cement briquette protection structure.
Key words:offshore oil and gasꎻ underwater facilitiesꎻ composite protective structure
收稿日期: 2021 ̄03 ̄31
基金项目: 深圳市 2020 年第一批技术攻关重点项目 (重 2020N014)
作者简介: 石锦坤 (1986 ̄)ꎬ 男ꎬ 学士ꎬ 高级工程师ꎬ 主要从事海洋石油工程设计和科研方面的工作ꎮ
通讯作者: 郭飞 (1991 ̄)ꎬ 男ꎬ 学士ꎬ 助理工程师ꎬ 主要从事海洋石油工程设计和科研方面的工作ꎬ guofei@cooec? com? cnꎮ
1 引 言
纤维增强复合材料是以树脂为基体材料ꎬ以纤
维为增强材料复合而成ꎬ其应用领域日益广泛ꎬ已从
航天航空、建筑建材、电子电器、轨道交通、石油化
工、汽车制造等传统领域扩展到风力发电、过滤除
尘、环境工程、海洋工程等新兴领域[1 ̄4]
ꎮ 玻璃纤维
增强复合材料具有重量轻、强度高、耐腐蚀、可设计
性强、表面光滑、不易生长海生物等适用于海洋环境
的特点ꎬ具有非常广阔的海洋油气开发水下生产设
施保护应用前景ꎮ
在海洋油气开发领域ꎬ以欧洲为主的石油公司
早在 20 世纪 90 年代就已开始将玻璃纤维增强复合
材料防护结构用于各类水下设施保护、膨胀弯和海
缆等管线防落物冲击、防渔网拖挂和海缆交叉点处
理等ꎬ如图 1 所示[5ꎬ6]
ꎮ
78 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
图 1 各类复合材料保护结构在海洋石油水下的应用
Fig? 1 Application of various types of composite
protection covers in the subsea of offshore oil
我国海域油气资源丰富ꎬ主要沉积盆地石油地
质资源 393? 22 亿吨、天然气 52? 61 万立方米ꎬ目前
已探明石油地质储量 52? 9 亿吨、天然气地质储量
1? 43 万亿立方米[7]
ꎮ 据统计ꎬ近 10 年来ꎬ由于落物冲
击、渔网拖挂等原因ꎬ水下油气设施损坏达 10 起以
上ꎬ每起事故造成的经济损失达上亿元ꎬ对水下生产
设施进行保护迫在眉睫ꎮ 国内海油工程水下生产设
施相关结构ꎬ如采油树、管汇终端、脐带缆终端等ꎬ目
前采取的防渔业保护结构均为钢结构形式ꎬ尚无国
产化复合材料防护结构水下实际应用案例ꎮ 随着海
洋油气开发的快速发展ꎬ对复合材料防护结构的需
求将呈现爆发式增长ꎮ
2 复合材料水下防护结构在海洋油气开发
中的应用
国际上对水下油气生产设计防护有着较为丰富
的防护和设备研制经验ꎮ 1992 年ꎬ挪威 Seanor 公司
为壳牌设计了首个复合材料井口装置保护罩ꎬ如图
2 所示ꎮ 如采用钢结构形式ꎬ为了能够满足水下机
器人(ROV) 维保和操作要求ꎬ边长尺寸较大ꎬ约为
15 mꎮ 采用复合材料形式后ꎬ其重量减少到钢结构
重量的 1 / 4ꎬ保护罩边长可以减小到为 10 mꎬ而且保
护罩可以通过底边的销轴翻转打开ꎬ从而满足 ROV
操作需求ꎮ 相对于钢结构形式ꎬ该复合材料保护罩
为壳牌节约了 20%的费用[8]
ꎬ从此复合材料在海洋
油气水下设施防护领域开始得到广泛应用ꎮ
图 2 Seanor 公司复合材料井口保护罩
Fig? 2 Seanor′s composite wellhead protection cover
目前ꎬ在海洋油气领域ꎬ复合材料生产厂家主要
集中在挪威、英国等北欧国家ꎬ主要包括挪威 CSUB、
Glassfiber、Komtek、Compoceanꎬ英国 PJNC 和立陶宛
Highcomp 公司等ꎮ 由于渔业发展迅速ꎬ渔业活动如
渔网渔具拖挂和落锚等对海洋油气水下设施的影响
较大ꎬISO 13628 ̄15 标准明确说明由于渔业捕捞装
置的发展ꎬ各项目需对当下和将来的渔业活动进行
评估ꎬ一般水深低于 750 m 时ꎬ水深需对渔具拖挂和
落物进行防护ꎮ
根据水下应用用途ꎬ复合材料防护结构主要可
以分为撬块保护罩、海底管缆保护罩、水下跨接管保
护罩、舱口盖、支撑装置等ꎮ
2? 1 撬块保护罩
撬块保护罩主要用于保护水下管汇、基盘、脐带
缆终端等水下设施ꎬ以抵抗落物、渔网和渔具等第三
方活动造成的机械损伤ꎮ 对于大型水下设施ꎬ钢结构
保护罩重量较大ꎬ运输和安装费用高ꎬ而复合材料相
对重量只有钢结构的 1 / 4 ~ 1 / 3ꎬ大大降低了运输和
安装等施工成本ꎮ 同时相对于钢结构ꎬ复合材料抗震
性能较好ꎬCSUB 公司成功试验并交付了可承受 300 kJ
和 500 kJ 冲击能量的水下撬块保护罩产品ꎬ并完成
了 800 kJ 冲击能量的保护罩产品设计ꎮ 目前其制造
完成的最大撬块保护罩尺寸为 30 m×15 m
[9]
ꎮ Sub ̄
sea7 公司采用复合材料设计水下撬块ꎬ钢结构重量
从 140 t 降低到 40 tꎬ降低了制造和安装成本ꎮ
撬块保护罩的形式主要包括整体式和分体式两
种ꎬ如图 3 所示ꎮ 整体式保护罩一般在上方留有 ROV
操作的舱门或可整体打开ꎬ方便 ROV 维保和操作ꎻ
分体式撬块保护罩一般结构较大ꎬ需要分体吊装入
水ꎬ入水后再通过销轴等形式组装为一体ꎮ 保护罩
的两侧留有海管或海缆接入口ꎬ并留有一定间隙ꎬ从
而保证海管或海缆有移动空间ꎮ
(a)整体式
2021 年第 12 期 79
???????????????????????????????????????????????
复合材料水下防护结构在海洋油气开发的应用
(b)分体式
图 3 撬块保护罩
Fig? 3 Skid protection cover
2? 2 海底管缆保护罩
海底管缆主要包括海管和海缆ꎬ一般通过挖沟、
落石或水泥压块保护ꎻ但当海底管缆受高温高压影
响时ꎬ将导致海管膨胀弯或海缆端部发生移动ꎬ如果
通过水泥压块或落石保护ꎬ将导致端部法兰应力集
中ꎬ因此需为管缆端部段留有一定的移动空间ꎬ采用
如图 4 所示复合材料保护罩形式可以较好地解决这
一问题ꎮ
图 4 海底管缆保护罩
Fig? 4 Subsea pipe /cable protection cover
复合材料保护罩的外形具有较好可塑性ꎬ通常海
底管缆的复合材料保护罩两端为半球形式ꎬ各个保护
罩通过相互球式铰接配合ꎬ从而保证了多个保护罩
的整体性能ꎬ而且铰接连接的保护罩可以随着管缆
移动而转动ꎮ 管缆保护罩一般数量较多ꎬ为了运输
和安装方便ꎬ可堆叠运输并在海上一同入水ꎬ再进行
海底分片安装ꎬ大大节省了运输和安装费用[10]
ꎮ
随着海底设施的增多ꎬ铺设新增的海底管缆与
在位的管缆容易产生交叉ꎬ为了保证管缆之间相互
不产生影响ꎬ通常需对交叉点进行处理ꎮ 可以通过
安装如图 5 所示复合材料交叉点跨接板件起到两条
管缆相互分隔的作用ꎮ
图 5 海缆交叉点跨接板件
Fig? 5 Composite cable crossing structures
2? 3 水下跨接管保护罩
水下跨接管是一种海底连接设备ꎬ可连接采油
树和管汇等撬块ꎬ也可在连接海管终端时同时起到
输送油气和吸收海管热胀冷缩量的作用ꎮ 当跨接管
采用垂直连接器时ꎬ其优势是便于安装ꎬ劣势是由于
跨接管的形状多设计成比较高耸的 M 型ꎬ当跨接管
受到较小的拖网拉力即会损坏ꎬ可能导致泄漏停产
的风险ꎮ 水下跨接管复合材料保护罩如图 6 所示ꎬ通
过复合材料对跨接管的整体包覆减小拖挂损坏风险ꎮ
图 6 跨接管保护罩
Fig? 6 Subsea jumper protection cover
2? 4 复合材料舱口盖
如图 7 所示为复合材料舱口盖ꎬ通常用于保护
采油树、水下管汇等水下设施ꎮ 复合材料舱口盖通
过销轴等结构连接到防护结构上ꎬ与传统钢结构舱
口盖对比ꎬ复合材料舱口盖重量轻可整体打开ꎬ方便
ROV 对水下设施进行操作和维保ꎬ而且具有吸收冲
击能量高等优点ꎮ
80 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
图 7 复合材料舱口盖
Fig? 7 Subsea composite protection hatches
2? 5 复合材料支撑装置
由于海床环境复杂ꎬ在软质海床上ꎬ为了保证海底
管缆、水下结构或设备着床时不沉入海床ꎬ可在其下
方铺放复合材料支撑装置ꎬ如图 8 所示ꎬ从而提高支
撑能力ꎮ 支撑板件也可以用于消除海管屈曲、减少海
管与泥面摩擦力ꎬ从而允许海管随温度变化而自由膨
胀变形ꎮ复合材料支撑装置按功能主要分为防沉板、悬
链线支撑板、悬跨基础和立管着泥段支撑板件等ꎬ可
批量生产以及堆叠运输ꎬ大大降低了制造和安装成本ꎮ
图 8 复合材料支撑装置
Fig? 8 Composite support structures
3 复合材料防护结构水下应用特点
海洋油气水下设施防护结构主要包括钢结构防
护形式(见图 9)、水泥压块防护形式(见图 10)以及
复合材料防护形式ꎬ表 1 对三种防护形式的优缺点进
行了对比ꎮ
图 9 钢结构防护形式
Fig? 9 Protection of steel structure
图 10 钢结构和水泥压块保护形式
Fig? 10 Protection of concrete mattress
表 1 不同防护形式优缺点对比
Table 1 Comparison of advantages and disadvantages of different forms of protection
形式 复合材料 钢结构 水泥压块
主要
用途
1.各类水下设施防护结构
2.管缆防落物冲击、防渔网拖挂
3.交叉点处理
1.各类水下结构物防护结构
2.管缆防落物冲击、防渔网拖挂
3.交叉点处理
1.管缆防落物冲击
2.交叉点处理
优点
1.耐化学腐蚀ꎬ寿命长
2.轻质高强ꎬ为钢结构重量的 30% ~50%ꎬ节省安装成本
3.设计灵活性大、表面光滑ꎬ防渔网拖挂、不易生长海生物
4.吸收冲击能量大、抗疲劳
5.耐高低温
6.可堆叠运输
7.采用同一模具批量生产ꎬ造价低、周期短
1.结构强度高
2.形状尺寸易修改
1.预制周期短
2.安装方便
3.价格较低
缺点
1.成型后ꎬ不易修改尺寸
2.需安装配重(水泥配重或落石)
1.需阳极防腐
2.结构重量大
3.预制周期较长
4.建造和安装成本较高
1.无法防渔具拖挂
2.与管缆接触ꎬ落物载荷直接传递至管线
3.限制管缆位移ꎬ导致连接点处应力集中
(下转第 128 页)
2021 年第 12 期 81
???????????????????????????????????????????????
某型无人机复合材料机翼结构尺寸优化设计
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 013
某型无人机复合材料机翼结构尺寸优化设计
沈浩杰ꎬ 陈 刚ꎬ 夏 杨
(南京模拟技术研究所ꎬ 南京 210016)
摘要: 本文对无人机复合材料后掠机翼结构进行尺寸优化设计ꎮ 该机翼采用双闭室矩形梁式布局ꎮ 采用商用分析软件ꎬ
优化各分区 T800 碳纤维编织布预浸料 45°与 0°铺层的厚度与翼肋宽度ꎮ 优化模型选取机翼结构的强度与刚度作为约束条
件ꎬ结构重量最小作为优化目标ꎮ 选用蔡 ̄吴准则作为复合材料失效判定准则ꎮ 优化结果符合机翼主要零件的传力特点ꎬ满足
复合材料机翼的设计要求ꎮ
关键词: 无人机ꎻ 复合材料机翼ꎻ 尺寸优化设计ꎻ 蔡 ̄吴准则
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0082-07
Size optimization design of composite wing for UAV
SHEN Hao ̄jieꎬ CHEN Gangꎬ XIA Yang
(Nanjing Institute of Simulation Technologyꎬ Nanjing 210016ꎬ China)
Abstract:In order to deduce the structure weight and perform the properties of composite in the swept wing
structure for UAVꎬ the size optimization was conducted in the wing configuration with a double closed cell rectangu ̄
lar beam in the specific position. The composite wing adopted T800 carbon fiber woven clothes. Through commercial
software MSC. Patran and Nastranꎬ 89 variablesꎬ the thicknesses of 45° and 0° in different subareas and the widths
of ribs were optimized to minimize the structure weight. The constraints of the optimized model included the strength
and stiffness of the wing structure. The Tsai ̄Wu failure criterion was utilized to calculate the damage factors and de ̄
termine the damage of composite structure. The optimized results satisfied the characteristics of force transmission
within the main components of the swept wingꎬ and met the strengthꎬ stiffness and weight requirements of the com ̄
posite wing.
Key words:UAVꎻ composite wingꎻ size optimizationꎻ Tsai ̄Wu failure criterion
收稿日期: 2021 ̄08 ̄24
作者简介: 沈浩杰 (1988 ̄)ꎬ 男ꎬ 博士ꎬ 工程师ꎬ 主要从事无人机总体结构设计、 复合材料结构设计与分析方面的研究ꎬ shhaojie
@126? comꎮ
1 前 言
先进复合材料具有比强度高、比模量大等优点ꎬ
已被广泛应用于航空结构中ꎮ 机翼为固定翼无人机
的主承力部件ꎮ 随着对无人机性能要求的提升ꎬ复
合材料机翼已成为机翼结构轻量化设计的主流发展
方向ꎮ 结构设计充分利用了复合材料可设计性强的
特点ꎬ充分发挥了复合材料的优点ꎬ实现了复合材料
机翼结构优化设计ꎮ
大量学者针对复合材料机翼优化设计进行探索
研究ꎮ 主流优化策略为结合布局优化与尺寸优化的
两级优化模型[1 ̄6]
ꎮ 何林涛等[1]采用改进遗传算法ꎬ
结合两级优化模型对复合材料机翼进行优化设计ꎮ
柴红普[2] 选取机翼典型结构ꎬ采用自由尺寸优化方
法ꎬ对复合材料层压板进行优化设计研究ꎮ 常楠等[3]
采用 Patran / Nastran 商业软件ꎬ通过两级交替优化策
略完成复合材料机翼蒙皮优化ꎮ 刘波等[4]完成了机
翼的参数化建模ꎬ并采用机翼布局的两级优化方法
进行优化并验证ꎮ 众多学者[7 ̄14] 进行了复合材料铺
层优化研究ꎬ优化复合材料铺层数与铺层顺序ꎮ
某复合材料机翼采用双闭室矩形梁式布局ꎬ如
图 1 所示ꎮ 机翼材料选用 T800 碳纤维编织复合材
料ꎮ 外形尺寸为 2200 mm×1050 mm×100 mm(长×
宽×高)ꎮ 重量要求结构质量≤10 kgꎮ 强度与变形
要求在给定气动载荷分布下ꎬ结构不出现破坏及不可
恢复变形ꎬ机翼翼尖挠度≤56 mmꎬ扭转角≤1? 55°ꎮ
82 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
图 1 双闭室矩形梁式机翼布局
Fig? 1 Wing configuration with a double closed cell rectangular beam
该机翼复合材料板件厚度较小ꎬ铺层顺序优化
空间有限ꎮ 矩形梁的铺层一体性要求致使不同铺层
间结构关联性约束多ꎬ不适用文献中的铺层顺序优
化方法ꎬ将根据尺寸优化的铺层数量与相关约束进
行详细设计ꎮ
本文针对双闭室矩形梁式复合材料机翼ꎬ使用
商用软件进行分区尺寸优化设计ꎬ获得不同分区编
织布预浸料 45°与 0°铺层的厚度与翼肋宽度ꎬ见图
1ꎮ 通过对比优化前后的结构性能ꎬ说明尺寸优化后
复合材料机翼能够满足设计要求ꎮ
2 机翼结构
复合材料机翼中双闭室矩形梁承担最主要的载
荷ꎬ结构示意图如图 2 所示ꎮ 矩形梁上下缘条承担机
翼总体弯矩造成的轴向力ꎻ矩形梁腹板承担机翼的
剪力ꎻ矩形梁的闭室传递机翼的大部分扭矩ꎻ梁内填
充的泡沫起到提高机翼整体稳定性的作用ꎻ翼根设
置加强肋ꎬ承担后掠机翼的弯矩分量ꎮ 在机翼前后缘
分别布置了一定数量的翼肋:机翼根部后缘翼肋为
加强肋ꎬ对副翼传动系统提供支撑ꎻ其余翼肋起到传
递蒙皮受到的气动载荷及提高蒙皮稳定性的作用ꎮ
图 2 双闭室矩形梁结构示意图
Fig? 2 Double closed cell rectangular beam diagram
根据初步设计的强度计算结果ꎬ矩形梁前中后
腹板位置为弦长的 20%、41%和 66%处ꎬ其中 41%处
位置为机翼翼型的最大高度处ꎮ 前缘翼肋的位置为
外段机翼展长的 22? 1%、34? 3%、54? 2% 和 76? 0%
处ꎬ后缘翼肋位于外段机翼展长的 6? 5%、31? 6%、
54? 4%和 77? 2%处ꎬ具体布置如图 1 所示ꎮ
3 有限元模型
根据机翼构型ꎬ将整体机翼分为蒙皮、矩形梁腹
板、翼肋三部分ꎬ采用 MSC? Patran 与 Nastran 有限元
商用分析软件ꎬ对机翼进行建模分析ꎬ并自动对各结
构的尺寸进行优化设计ꎮ 其中ꎬ矩形梁上下部分材
料与机翼蒙皮相连接ꎬ优化过程中ꎬ将其视作整体进
行优化分析ꎮ
机翼的蒙皮、矩形梁腹板、翼肋腹板采用 Quad4
单元划分网格ꎬ翼肋缘条采用 Bar2 单元ꎮ 图 3 为高
性能靶机复合材料半机翼的有限元模型ꎮ
图 3 复合材料机翼有限元模型
Fig? 3 Finite element model of the composite wing
为了能够较准确地施加气动载荷ꎬ在气动计算时ꎬ
对机翼表面的加载区域进行划分:沿机翼弦向ꎬ将机
翼过渡段均分为两部分ꎬ将外机翼段均分为三部分ꎻ
沿机翼展向ꎬ将外机翼段均分为五部分ꎮ 总计划分 17
个区域ꎬ详细分区形式以及分区编号如图 4
[15]所示ꎮ
图 4 复合材料机翼加载区域划分
Fig? 4 Load zone division in the composite wing
攻角为 4°、Ma 数为 0.9 的工况下ꎬCFD 计算可
得各划分区域的升力与阻力的统计值ꎬ见表 1ꎮ
表 1 机翼各划分区域的气动力
Table 1 The aerodynamic load of each zone
区域
编号
升力
/ N
阻力
/ N
区域
编号
升力
/ N
阻力
/ N
01 678.89 17.79 31 1331.18 -78.35
02 1014.98 50.22 32 903.58 35.56
11 1066.18 -7.39 33 442.65 26.79
12 997.29 41.03 41 1226.18 -83.24
13 952.09 61.23 42 826.17 25.23
21 1284.62 -50.33 43 194.88 10.13
22 977.14 40.94 51 881.55 -80.29
23 664.04 43.28 52 526.79 12.98
53 10.17 9.31
2021 年第 12 期 83
???????????????????????????????????????????????
某型无人机复合材料机翼结构尺寸优化设计
建模选取左半机翼ꎬ故在机翼对称面处施加对
称位移约束ꎻ矩形梁式机翼通过 6 个螺栓与机身进行
连接ꎬ故在距离机翼对称面 150 mm 梁腹板的位置ꎬ
约束垂直于展向的两个平移自由度以及沿机翼展向
的转动自由度ꎬ具体加载与约束情况如图 5 所示ꎮ
图 5 复合材料机翼载荷与约束
Fig? 5 The load and constraint in the finite element model
机翼选用 T800 碳纤维编织复合材料ꎬ材料性能
如表 2 所示ꎮ
表 2 T800 碳纤维编织复合材料的基本力学性能
Table 2 Mechanical properties of T800 composite material
力学性能 值 力学性能 值
E1
/ GPa 80 XT1
/ MPa 1200
E2
/ GPa 80 XC1
/ MPa 900
v12 0.29 YT1
/ MPa 1200
G12
/ GPa 6 YC1
/ MPa 900
G23
/ GPa 2.5 S12
/ MPa 105
G13
/ GPa 6 S13
/ MPa 115
4 建立优化问题
以复合材料强度与机翼结构的变形为约束条
件ꎬ以复合材料机翼结构重量为目标函数ꎬ以机翼的
结构重量最小为优化目标ꎬ建立复合材料机翼结构
优化模型ꎬ优化机翼蒙皮、矩形梁腹板、翼肋的厚度
以及翼肋缘条的宽度ꎮ 机翼选用 T800 复合材料编
织布ꎬ铺层方向角选取 0°与 45°ꎮ 在优化过程中ꎬ将
机翼蒙皮、矩形梁腹板以及翼肋的 0°与 45°层的厚
度、翼肋缘条的宽度选取为设计变量ꎬ共计 89 个设
计变量ꎮ
优化迭代过程中ꎬ每一个计算步将对不同几何
尺寸的机翼模型进行计算分析ꎬ进而获得机翼的应
力分布与变形情况ꎮ 通过比较计算结果与约束条
件ꎬ结合优化算法ꎬ调整设计变量并重新进行计算ꎮ
直至计算结果满足收敛性条件ꎬ优化迭代过程结束ꎮ
4? 1 优化变量
模型中铺层形式采用[ 45 / 0] 的非对称铺层ꎮ
机翼蒙皮的铺层主方向为机翼展向沿后掠角方向ꎬ
考虑到 0°层为主承力层ꎬ故将 0°层置于机翼蒙皮内
侧ꎮ 该铺层与实际情况下 0°与 45°层交错铺层相比
较ꎬ模型中的分析设计偏安全ꎮ 矩形梁腹板的铺层
情况与机翼蒙皮相同ꎬ主方向为机翼展向ꎻ翼肋的铺
层主方向为机翼弦向ꎮ 优化模型中各单层的初始厚
度设定为 1 mmꎮ
优化变量选取范围的确定需结合考虑复合材料
加工工艺、复合材料铺层设计经验ꎮ 现将优化变量
选取范围汇总于表 3ꎬ变量区域示例如图 6 所示ꎮ
表 3 优化变量选取范围
Table 3 Variable range
优化变量 上界限/ mm 下界限/ mm
SKIN_12~ SKIN_16_T1(T2)
SKIN_42~ SKIN_46_T1(T2)
0.6 3
SKIN_21~ SKIN_26_T1(T2)
SKIN_31~ SKIN_36_T1(T2)
1 5
BEAM_11~ BEAM_16_T1(T2)
BEAM_21~ BEAM_26_T1(T2)
BEAM_31~ BEAM_36_T1(T2)
0.8 3
RIB_T1(T2) 1 3
RIB_W 10 20
注:“SKIN”表示机翼蒙皮ꎬ“BEAM”表示矩形梁腹板ꎬ“RIB”表示
翼肋ꎻ“T1”“T2”分别为 45°与 0°层的厚度ꎻ“RIB_W”为翼肋缘条宽度ꎮ
图 6 优化变量分区示意图
Fig? 6 Zone diagram of optimization variables
4? 2 约束条件
复合材料失效判定准则采用蔡 ̄吴准则ꎬ失效因
子 a 定义为:
84 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
(
1
XT
-
1
XC
)σ1
+ (
1
YT
-
1
YC
)σ2
+
1
XTXC
σ
2
1
+
1
YT YC
σ
2
2
+
1
S
2
σ
2
12
-
1
XTXC YT YC
σ1σ2
其中:XT 为纵向拉伸强度ꎻXC 为纵向压缩强度ꎻYT
为横向拉伸强度ꎻYC 为横向压缩强度ꎻS 为面内剪切
强度ꎻσ1 为纵向应力ꎻσ2 为横向应力ꎻσ12为面内剪
切应力ꎮ
复合材料结构安全系数定义为失效因子的倒
数ꎬ即 1 / aꎮ 选取结构安全系数为 1? 5ꎬ即 1 / a≥1? 5ꎬ
或复合材料失效因子 a≤0? 67ꎮ 变形约束为机翼翼
尖后缘挠度≤56 mmꎮ
5 优化结果
Nastran 经过 24 次计算迭代后ꎬ满足收敛条件ꎬ
给出优化设计结果ꎬ汇总于表 4ꎮ
表 4 双闭室矩形梁式机翼几何尺寸优化结果
Table 4 Size optimization result of the wing with a double closed cell rectangular beam
编 号 优化变量 数值/ mm 编 号 优化变量 数值/ mm 编 号 优化变量 数值/ mm
1 BEAM_11_T1 0.80 31 BEAM_34_T1 0.80 61 SKIN_23_T2 1.75
2 BEAM_11_T2 0.80 32 BEAM_34_T2 0.80 62 SKIN_24_T1 1.00
3 BEAM_12_T1 0.80 33 BEAM_35_T1 0.80 63 SKIN_24_T2 1.83
4 BEAM_12_T2 0.80 34 BEAM_35_T2 0.80 64 SKIN_25_T1 1.00
5 BEAM_13_T1 0.80 35 BEAM_36_T1 0.80 65 SKIN_25_T2 1.53
6 BEAM_13_T2 0.80 36 BEAM_36_T2 0.80 66 SKIN_26_T1 1.00
7 BEAM_14_T1 0.80 37 RIB_1_T1 1.27 67 SKIN_26_T2 1.00
8 BEAM_14_T2 0.80 38 RIB_1_T2 1.00 68 SKIN_31_T1 1.00
9 BEAM_15_T1 0.80 39 RIB_6_T1 1.00 69 SKIN_31_T2 3.82
10 BEAM_15_T2 0.80 40 RIB_6_T2 1.00 70 SKIN_32_T1 1.00
11 BEAM_16_T1 0.80 41 RIB_MID_T1 1.00 71 SKIN_32_T2 5.01
12 BEAM_16_T2 0.80 42 RIB_MID_T2 1.00 72 SKIN_33_T1 1.00
13 BEAM_21_T1 1.61 43 RIBSEC_MID_W 10.00 73 SKIN_33_T2 4.78
14 BEAM_21_T2 0.80 44 RIBSEC_ROOT_W 10.00 74 SKIN_34_T1 1.00
15 BEAM_22_T1 0.80 45 RIBSEC_TIP_W 10.00 75 SKIN_34_T2 3.82
16 BEAM_22_T2 0.80 46 SKIN_12_T1 0.60 76 SKIN_35_T1 1.00
17 BEAM_23_T1 0.80 47 SKIN_12_T2 0.60 77 SKIN_35_T2 2.61
18 BEAM_23_T2 0.80 48 SKIN_13_T1 0.60 78 SKIN_36_T1 1.00
19 BEAM_24_T1 0.80 49 SKIN_13_T2 0.60 79 SKIN_36_T2 1.00
20 BEAM_24_T2 0.80 50 SKIN_14_T1 0.60 80 SKIN_42_T1 0.60
21 BEAM_25_T1 0.80 51 SKIN_14_T2 0.60 81 SKIN_42_T2 0.60
22 BEAM_25_T2 0.80 52 SKIN_15_T1 0.60 82 SKIN_43_T1 0.60
23 BEAM_26_T1 0.80 53 SKIN_15_T2 0.60 83 SKIN_43_T2 0.60
24 BEAM_26_T2 0.80 54 SKIN_16_T1 0.60 84 SKIN_44_T1 0.60
25 BEAM_31_T1 3.89 55 SKIN_16_T2 0.60 85 SKIN_44_T2 0.60
26 BEAM_31_T2 1.11 56 SKIN_21_T1 1.00 86 SKIN_45_T1 0.60
27 BEAM_32_T1 0.97 57 SKIN_21_T2 1.00 87 SKIN_45_T2 0.60
28 BEAM_32_T2 1.00 58 SKIN_22_T1 1.00 88 SKIN_46_T1 0.60
29 BEAM_33_T1 0.86 59 SKIN_22_T2 1.57 89 SKIN_46_T2 0.60
30 BEAM_33_T2 0.80 60 SKIN_23_T1 1.00
2021 年第 12 期 85
???????????????????????????????????????????????
某型无人机复合材料机翼结构尺寸优化设计
6 结果分析
分别对各部件的优化结果进行分析ꎬ并对优化
结果的应力与刚度进行分析讨论ꎮ
前后缘蒙皮 0°层与 45°层厚度均达到优化变量
下界限值 0? 6 mmꎮ 矩形梁上下部分与蒙皮的连接
整体主要承担机翼弯矩ꎬ故 0°层是主承力层ꎬ45°层
厚度亦达到下界限值 1 mmꎮ 矩形梁前后闭室的 0°
层的厚度分布整体呈现出一定规律:从翼梢到翼根
逐渐变厚ꎮ 根据后掠翼机翼“前梁卸载、后梁加载”
的特点ꎬ后梁承担弯矩的传力路径较短ꎬ承担较大部
分的弯矩载荷ꎬ故矩形梁后闭室的 0°层与前闭室的
相比较厚ꎮ
矩形梁腹板主要传递机翼的剪切载荷ꎮ 随着从
翼梢到翼根气动载荷的累积ꎬ翼根位置的梁腹板需
采用较厚的 45°层ꎮ 优化结果显示ꎬ翼根处ꎬ后梁腹
板的厚度大于前梁与中梁ꎮ 前梁腹板以及中梁外段
腹板的厚度均达到优化变量的设定下限值 0? 8 mmꎮ
普通翼肋主要传递蒙皮所受气动载荷ꎬ防止前
后缘蒙皮失稳ꎬ故复合材料厚度在优化后均达到下
界限值ꎮ 机翼根部的加强肋传递后肋翼在翼根转折
处产生的弯矩分量ꎬ故 45°铺层超过下界限值ꎮ 翼
肋缘条宽度均为下界限值ꎮ
图 7、图 8 分别为优化前后机翼的应力云图与
失效因子云图ꎮ 应力云图展示了 45°层的应力分布
情况ꎬ该层出现最大应力ꎮ 经过对各部件几何尺寸
的优化ꎬ机翼模型的应力分布更加均匀ꎬ模型的最大
Von Mises 应力从 1070 MPa 下降至 498 MPaꎻ最大失
效因子从 1? 05 下降至 0? 28ꎬ小于 0? 67 的设计要求ꎻ
最危险点从上蒙皮与翼梁后腹板位移约束处转移至
上蒙皮和翼梁中腹板位移约束处ꎮ 图 9 为优化后机
翼各部件的应力云图ꎮ 图 10 为优化前后机翼的位
移云图ꎮ 翼尖最大变形从 103 mm 下降至 55? 9 mmꎬ
小于 56 mm 的设计要求ꎻ翼尖最大扭转角由 2? 94°
下降至 1? 31°ꎬ小于 1? 5°的设计要求ꎮ 综上所述ꎬ优
化结果满足复合材料机翼结构设计要求ꎮ
图 7 优化前初始几何参数下应力云图(a)与失效因子云图(b )
Fig? 7 The stress nephogram (a) and the failure factor nephogram (b) before optimization
图 8 优化后机翼的应力云图(a)与失效因子云图(b)
Fig? 8 The stress nephogram (a) and the failure factor nephogram (b) after optimization
86 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
图 9 优化后机翼各部件应力云图
Fig? 9 The stress nephograms of the wing components
图 10 优化前(a)与优化后(b)机翼的位移云图
Fig? 10 The displacement nephograms of the wing before optimization (a) and after optimization (b)
2021 年第 12 期 87
???????????????????????????????????????????????
某型无人机复合材料机翼结构尺寸优化设计
图 11 为优化迭代过程的机翼结构重量变化情
况ꎮ 从图中可以看出ꎬ通过优化ꎬ机翼结构重量从初
始设计变量下的 3? 68 kg 变为 4? 22 kgꎮ 需要说明的
是ꎬ初始状态的铺层厚度并不能满足设计要求ꎬ故优
化后结构重量有一定程度的上升ꎮ 机翼复合材料结
构重量为 8? 44 kgꎬ满足复合材料结构重量不大于 10
kg 的设计要求ꎮ
图 11 半机翼结构重量随优化迭代步的变化
Fig? 11 Weights of half of the wing with different iteration steps
综上所述ꎬ复合材料机翼的设计要求达成情况
详见表 5ꎮ
表 5 复合材料机翼设计要求达成表
Table 5 Achievement of requirements in the composite wing
序 号 设计要求 优化结果 是否满足
1 结构重量≤10 kg 8.44 kg 是
2 结构最大失效因子≤0.67 0.28 是
3 机翼最大变形≤56 mm 55.9 mm 是
7 结 论
(1)本文根据复合材料机翼的双闭室矩形梁布
局形式ꎬ选取机翼结构的强度与刚度作为约束条件ꎬ
结构重量最小作为优化目标ꎮ
(2)设定 89 个优化变量ꎬ包括各分区 45°与 0°
铺层的厚度与翼肋宽度ꎬ进行分区尺寸优化ꎬ优化迭
代次数较少ꎬ速度较快ꎮ
(3)对优化结果进行分析ꎬ该结果符合机翼主
要零件的传力特点ꎬ并满足机翼的设计要求ꎮ
参考文献
[ 1] 何林涛ꎬ 万小朋ꎬ 赵美英. 布局优化和尺寸优化相结合的复合材
料机翼优化设计[J]. 中国机械工程ꎬ 2008ꎬ 19(17): 2077 ̄2080.
[2] 柴红普. 复合材料层压板典型结构优化设计研究[D]. 上海: 上
海交通大学航空航天学院ꎬ 2011.
[3] 常楠ꎬ 赵美英ꎬ 王伟ꎬ 等. 基于 PATRAN/ NASTRAN 的复合材料
机翼蒙皮优化设计[J]. 西北工业大学学报ꎬ 2006ꎬ 24(3): 326 ̄329.
[4] 刘波ꎬ 陆振玉ꎬ 袁东明ꎬ 等. 复合材料无人机机翼布局的二级化
化方法[J]. 玻璃钢/ 复合材料ꎬ 2016(4): 31 ̄35.
[5] 乔巍ꎬ 姚卫星. 复合材料加筋板铺层优化设计的等效弯度刚度
法[J]. 计算力学学报ꎬ 2011ꎬ 28(1): 158 ̄162.
[6] 程文渊ꎬ 常艳ꎬ 崔德刚ꎬ 等. 基于分布式计算的复合材料机翼优
化设计[J]. 复合材料学报ꎬ 2007(1): 167 ̄171.
[7] 修英姝ꎬ 崔德刚. 复合材料层合板稳定性的铺层优化设计[ J].
工程力学ꎬ 2005(6): 212 ̄216.
[8] 朱胜利ꎬ 刘红武ꎬ 邱宏波. 基于复合材料机翼刚度的铺层自由尺
寸优化分析[J]. 航空工程进展ꎬ 2012(1): 55 ̄59.
[9] HIRANO Yꎬ TODOROKI A. Fractal branch and bound method for
stacking ̄sequence optimization of composite delta wing[ C] / / AIAA
1st Intelligent Systems Technical Conference. 2004.
[10] MESGNITAꎬ KAMAT M P. Optimum of stiffened laminated com ̄
posite plates with frequency constrains[J]. Engineering Optizationꎬ
1987ꎬ 11(1): 77 ̄88.
[11] ABOUHAMZE Mꎬ SHAKERI M. Multi ̄objective stacking sequence
optimization of laminated cylindrical panels using a genetic and
neural networks[J]. Composite Structuresꎬ 2007ꎬ 63: 339 ̄345.
[12] DIANZI Lꎬ VASSILI Tꎬ OSVALDO M Qꎬ et al. Bi ̄level optimiza ̄
tion of blended composite wing panels [ J]. Journal of Aircraftꎬ
2011ꎬ 48(1): 107 ̄118.
[13] LIU Dꎬ TOROPOV Vꎬ MING Zꎬ et al. Optimization of blended
composite wing panels using smeared stiffness technique and lami ̄
nation parameters[C] / / 51st AIAA/ ASME/ ASCE/ AHC/ ASC Struc ̄
turesꎬ Structural Dynamics & Materials Conference. 2010.
[14] 韩庆ꎬ 王广博ꎬ 钟小平ꎬ 等. 基于遗传算法的复合材料泡沫夹
层板铺层优化设计[J]. 航空工程进展ꎬ 2013(2): 182 ̄185.
[15] 陈刚ꎬ 王校培ꎬ 宋军ꎬ 等. 某高载荷大后掠无人机复合材料机
翼结构设计与试验验证[ J]. 南京航空航天大学学报ꎬ 2021ꎬ
53(4): 613 ̄619.
88 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
DOI:10? 19936 / j? cnki? 2096 ̄8000? 20211228? 014
湿法分层缠绕 T700 / 环氧复合材料微波固化工艺及性能
李梦颖ꎬ 肖 军∗
ꎬ 还大军ꎬ 王兴邦ꎬ 杨 潇ꎬ 焦 洋
(南京航空航天大学 材料科学与技术学院ꎬ 南京 210016)
摘要: 针对大厚度固体火箭发动机壳体制造周期长的缺点ꎬ本文提出分层缠绕微波预固化工艺ꎮ 以固化度为依据ꎬ结合
壳体缠绕规律及微波吸收效率ꎬ筛选出[90° 2
/ ±20°]的分层缠绕基元ꎮ 分层缠绕中需经多次微波辐射ꎬ考虑热传导或弱微波效
应对已缠绕层固化度的影响ꎬ制定出升温速率为 5 ℃ / min、由室温升至 90 ℃的微波预固化工艺ꎬ后处理采用热固化:160 ℃ 保
温 1 hꎮ 在微波固化试样制备时间(均不考虑降温时间)比热固化缩短近一半的情况下ꎬT700 碳纤维复合材料微波固化与热固
化试样力学性能基本一致:微波固化层合板拉伸强度为 1? 84 GPaꎬ热固化层合板拉伸强度为 1? 76 GPaꎻ微波固化层合板弯曲
强度为 1? 20 GPaꎬ热固化层合板弯曲强度为 1? 17 GPaꎻ微波固化 NOL 环拉伸强度为 2? 94 GPaꎬ热固化 NOL 环拉伸强度为 3? 08
GPaꎻ微波固化 NOL 环层间剪切强度为 76? 1 MPaꎬ热固化 NOL 环层间剪切强度为 75? 6 MPaꎮ 扫描电镜照片表明ꎬ两种固化方
式下纤维 ̄基体界面结合良好ꎮ 由于微波固化不依赖于热传导或热对流ꎬ因此可以在较短的时间内达到与热固化试样相当的
力学性能ꎮ
关键词: 固体火箭发动机壳体ꎻ 碳纤维复合材料ꎻ 湿法分层缠绕工艺ꎻ 微波固化ꎻ 热固化ꎻ 力学性能
中图分类号: TB332 文献标识码: A 文章编号: 2096-8000(2021)12-0089-06
Microwave curing process and properties of T700 /epoxy composites by wet filament lamination winding
LI Meng ̄yingꎬ XIAO Jun
∗
ꎬ HUAN Da ̄junꎬ WANG Xing ̄bangꎬ YANG Xiaoꎬ JIAO Yang
(College of Materials Science and Technologyꎬ Nanjing University of
Aeronautics and Astronauticsꎬ Nanjing 210016ꎬ China)
Abstract:In this paperꎬ the rapid manufacturing of large ̄size solid rocket motor shell is the research back ̄
ground. Aiming at the problems of long curing cycle and high production cost in traditional heat curingꎬ a layered
microwave pre ̄curing process is proposed to shorten the manufacturing cycle and maintain excellent performance.
With the help of differential scanning calorimeterꎬ based on the curing degreeꎬ combined with the shell winding law
and microwave absorption efficiencyꎬ the layered winding element of [90°2
/ ±20°] was selected. Considering the in ̄
fluence of heat conduction and microwave effect on the curing degree of the wound layerꎬ a microwave pre ̄curing
process with heating rate of 5 ℃ / min and rising from room temperature to 90 ℃ was determined. The post ̄treatment
was heat curing by holding at 160 ℃ for 1 h. Microwave curing and heat curing composite laminates and NOL rings
were prepared. When the preparation time of samples cured by microwave (regardless of cooling time) is nearly half
shorter than that of samples cured by heatꎬ the mechanical properties of samples cured by microwave and heat are
basically the same. Because of the bulk heating characteristics of microwave curingꎬ it can achieve the mechanical
properties equivalent to that of the heat cured samples in a short time.
Key words:solid rocket motor shellꎻ carbon fiber compositesꎻ wet layered windingꎻ microwave curingꎻ heat
curingꎻ mechanical properties
收稿日期: 2021 ̄04 ̄01
作者简介: 李梦颖 (1995 ̄)ꎬ 女ꎬ 硕士ꎬ 实验员ꎬ 主要从事先进树脂基复合材料方面的研究ꎮ
通讯作者: 肖军 (1959 ̄)ꎬ 男ꎬ 博士ꎬ 教授ꎬ 主要从事聚合物基复合材料方面的研究ꎬ 包括自动铺放技术与装备、 先进缠绕技术等ꎬ
j? xiao@nuaa? edu? cnꎮ
固体火箭发动机是一种采用固体推进剂的化学
火箭动力装置ꎬ在导弹武器、运载火箭和空间飞行器
中都有广泛应用[1ꎬ2]
ꎮ 固体火箭发动机壳体既是存
贮推进剂的贮箱ꎬ又是推进剂燃烧的场所ꎬ须承受复
杂的外力和环境条件引起的载荷[3]
ꎮ 碳纤维/ 环氧
复合材料比强度高、比模量高、耐高温、耐腐蚀、抗疲
劳、力学性能优异[4 ̄6]
ꎬ因此第四代固体火箭发动机
普遍采用碳纤维/ 环氧复合材料壳体ꎮ
2021 年第 12 期 89
???????????????????????????????????????????????
湿法分层缠绕 T700 / 环氧复合材料微波固化工艺及性能
目前ꎬ大尺寸复合材料回转体构件多采用“分层
缠绕预固化+最终热固化”的成型工艺ꎬ由于采用热
传导的加热方式ꎬ存在固化周期长、能量损耗高等缺
点ꎬ极大地限制了树脂基复合材料在大尺寸构件上
的应用[7]
ꎮ 先进树脂基复合材料领域迫切需要高
效、省时、环保的制造工艺ꎬ快速固化技术应运而生ꎮ
微波固化具有加热效率高、选择性加热、清洁环保[8 ̄11]
等特点ꎬ近年来在复合材料领域发展迅速ꎬ也被越来
越多的研究者重视[12 ̄15]
ꎮ Kwak 等[16]和 Ma 等[17] 的
研究结果表明:在固化时间显著缩短的情况下ꎬ微波
固化碳纤维增强环氧树脂复合材料的力学性能与热
固化试样基本相当ꎬ甚至略高ꎮ 然而ꎬ随着研究的深
入ꎬ微波固化碳纤维复合材料的难点逐渐被人们熟知ꎮ
Chinedum 等[18]指出碳纤维固有的介电特性阻止微
波穿透复合材料ꎬ在厚度方向上起到微波屏蔽的作
用ꎮ 这将不利于碳纤维复合材料的微波固化ꎮ
针对大尺寸固体火箭发动机壳体ꎬ本文提出“分
层缠绕微波预固化+最终热固化”工艺ꎬ不仅能够缩
短固化时间ꎬ还能弱化碳纤维复合材料厚度方向上
的微波屏蔽问题ꎮ本文首先根据固化度筛选出微波吸
收性较好的铺层[90°2
/ ±a°]ꎬ接下来以[90°2
/ ±a°]
为基元制定微波预固化工艺ꎬ最后对比分析微波固
化和热固化碳纤维复合材料层合板、NOL 环的力学
性能以及显微组织ꎮ
1 试验部分
1? 1 试验材料及设备
TDE ̄85 型三官能团环氧树脂ꎬ环氧值不小于 0?85ꎬ
AFG ̄90H 型三官能团环氧树脂ꎬ环氧值为 0? 95 ~
1? 05ꎬ生产商均为上海华谊树脂有限公司ꎻ固化剂为
甲基六氢苯酐(MeHHPA)ꎬ生产商为广州市深创化
工有限公司ꎻ促进剂为 2ꎬ4ꎬ6 ̄三(二甲胺基甲基)苯
酚(DMP ̄30)ꎬ生产商为上海麦克林生化科技有限公
司ꎻ试验所用碳纤维为日本东丽 T700SC ̄24000ꎬ线
密度为 1650 g / 1000 mꎮ
试验仪器及设备见表 1ꎮ
表 1 试验设备
Table 1 Test equipment
设备名称 型 号 生产商
排布机 - 西安龙德科技发展有限公司
差示扫描量热仪 200F3 德国 NETZSCH 公司
微波固化炉 - 自 制
热固化炉 ZKXFB ̄2 上海树立仪器仪表有限公司
电子万能试验机 CMI5150 深圳新三思公司
电子显微形貌仪 DVM ̄6A 德国 Leica 公司
扫描电子显微镜 S ̄4800 日本 Hitachi 公司
本实验所使用的设备是一台高性能八面体微波
炉ꎬ由 Li 的研究团队[15] 设计制造ꎮ 它有 16 个独立
的微波源ꎬ工作频率为 2? 45 GHz±50 MHzꎬ均匀分布
在谐振腔周围ꎮ 采用红外热像仪和光纤荧光传感器
对复合材料的温度进行监测ꎮ 利用红外热像仪观察
微波固化炉中的复合材料是否出现打火现象ꎬ以确
保试验的安全性ꎮ 采用五个光纤荧光传感器对复合
材料的表面温度进行监测ꎬ以平均值作为监测温度ꎮ
根据监测温度与复合材料设定温度的差异ꎬ通过实
时调节微波功率来控制加热速率ꎮ
1? 2 试样制备
1? 2? 1 预浸料制备
检查并清理排布机ꎬ将碳纤维置于放纱辊ꎬ将配
制好的环氧树脂倒入胶槽ꎮ 设置排布机参数:张力设
定为 10 Nꎬ排布螺距为 8? 5 mmꎬ走纱速度为 5 mm/ sꎮ
碳纤维经展纱辊、胶辊和匀胶辊ꎬ最终缠绕到收卷装
置上ꎬ即可得到 T700 碳纤维单向预浸料ꎬ如图 1 所示ꎮ
图 1 T700 碳纤维单向预浸料
Fig? 1 T700 carbon fiber unidirectional prepreg
1? 2? 2 复合材料层合板制备
按照设计的尺寸、角度、数量裁剪预浸料并铺至
规定厚度ꎮ 以钢化玻璃作为模具ꎬ采用真空袋压成
型技术分别按照一定的工艺曲线进行微波固化和热
固化ꎬ将固化后的层合板切割至标准中规定的尺寸ꎮ
1? 2? 3 复合材料 NOL 环制备
采用实验室自制的 NOL 环缠绕平台(示意图如
图 2 所示) 和 NOL 环模具(实物如图 3 所示) 制备
NOL 环ꎬ然后分别按照一定的工艺曲线进行微波固
化和热固化ꎮ
图 2 NOL 环缠绕平台示意图
Fig? 2 Schematic diagram of NOL ring winding platform
90 2021 年 12 月
???????????????????????????????????????????????
复合材料科学与工程
图 3 NOL 环单环模具实物图
Fig? 3 Physical picture of NOL ring single ring mould
1? 3 测试方法
固化度测试:采用差示扫描量热仪以 10 ℃ / min
的升温速率对复合材料的固化反应进行测试ꎬ复合
材料固化度计算公式如下:
α =
ΔH1
- ΔH2
ΔH1
× 100% (1)
式中:α 为复合材料的固化度ꎬ%ꎻΔH1为预浸料完全
固化后的总放热焓ꎬJ/ gꎻΔH2为已固化复合材料的剩
余放热焓ꎬJ/ gꎮ
层合板性能测试:拉伸性能采用电子万能试验
机按照 GB / T 3354—2014 测试ꎬ弯曲性能按照 GB / T
3356—2014 测试ꎬ层间剪切性能按照 GB / T 30969—
2014 测试ꎮ
NOL 环性能测试:采用电子万能试验机按照 GB/
T 1458—2008 测试ꎮ
孔隙含量和纤维体积含量测试:采用电子显微形
貌仪按照 GB/ T 3365—2008 测试ꎮ对复合材料试样进
行打磨、抛光ꎬ然后使用显微形貌仪对截面进行拍摄ꎮ
使用 Image J 软件对图片进行处理ꎬ从而得到纤维体
积含量ꎬ孔隙含量测试方法与纤维体积含量测试方
法相同ꎮ 纤维体积含量测试原理如下列公式所示:
Vf
=
∑
n
i = 1
Vfi
n
× 100% (2)
式中:Vf为纤维体积含量ꎬ%ꎻVfi为第 i 个观测面内纤
维体积含量ꎬ%ꎻn 为试样观测面个数ꎮ
2 结果与讨论
结合缠绕规律及微波吸收效率ꎬ同时考虑试验
的可操作性ꎬ本试验以[90°2
/ ±a°]的铺层方式为基
元ꎬ以平板件代替缠绕件制定分层微波预固化工艺ꎮ
2? 1 确定最佳缠绕角度
当电磁波辐射到复合材料上时ꎬ一部分波被反射ꎬ
一部分被材料吸收ꎬ其余部分透过材料ꎮ 反射、透射
和吸收的能量取决于材料的复介电常数、层数、铺层
角度和入射电磁波的特性[19]
ꎮ 本试验中材料确定ꎬ
缠绕中重复单元[90°2
/ ±a°]确定(即层数确定)ꎬ入
射电磁波频率(2? 45 GHz)确定ꎮ 因此ꎬ需要研究碳
纤维复合材料中铺层角度对吸波性能的影响ꎮ 采用
相同的微波工艺固化铺层方式为[90°2
/ ±a°] ( a° =
0°、10°、20°、30°、40°、50°、60°、70°、80°、90°)的层合
板ꎬ以固化度为评价标准ꎬ选出吸波性最佳的铺层ꎮ
铺层方式为[90°2
/ ±a°]的碳纤维/ 环氧复合材
料的固化度变化如图 4 所示ꎮ 图 4 表明:碳纤维复合
材料层合板固化度的变化随铺层角度的改变没有一
定规律ꎬ[90°2
/ ±20°]的层合板固化度最高ꎬ为 49? 8%ꎬ
表明该铺层方式下吸波效率最高ꎮ 王晓红等[20] 详
细研究了连续碳纤维复合材料的微波电磁特性及雷
达波反射特性ꎬ指出当入射电场沿碳纤维方向时ꎬ复
合材料反射损耗基本为 0 dBꎬ反射率最大ꎻ当入射电
场垂直碳纤维方向时ꎬ反射损耗最大ꎬ吸波性较好ꎮ
微波固化炉中电场方向随时间不断变化ꎬ与铺层方
式为[90°2
/ ±20°]的复合材料耦合时ꎬ垂直纤维方向
的电场分量较大ꎬ反射率相对较小ꎬ宏观上表现为该
铺层方式的碳纤维/ 环氧复合材料的固化度较高ꎮ
图 4 铺层方式为[90° 2
/ ±a°]的碳纤维/ 环氧
复合材料的固化度变化曲线
Fig? 4 Curing degree curve of carbon fiber/epoxy composite
with [90° 2
/ ±a°] laminating method
2? 2 确定分层微波预固化工艺
以铺层方式为[90°2
/ ±20°]的碳纤维/ 环氧复合
材料为研究对象ꎬ制定其固化度达到 70% ~ 80%时
的微波预固化工艺ꎮ 文献[21] 指出微波加热适宜
的升温速率为 1 ℃ / min ~ 8 ℃ / minꎮ 热固性树脂基
复合材料阶段升温工艺中ꎬ第一个升温阶段树脂主
要发生物理变化ꎬ同时考虑加热效率ꎬ因此第一个升
温阶段采用 5 ℃ / min 的升温速率ꎮ 第一个保温阶
段的目的是使树脂充分浸渍纤维ꎬ对应树脂黏度最
低点的温度ꎬ由树脂的黏度 ̄温度曲线确定ꎬ如图 5
2021 年第 12 期 91
???????????????????????????????????????????????
湿法分层缠绕 T700 / 环氧复合材料微波固化工艺及性能
所示ꎮ 加热到 90 ℃时ꎬ环氧树脂的黏度最低ꎮ 以固
化度为指标ꎬ确定第一个阶段的保温时间ꎮ 铺层方
式为[90°2
/ ±20°]的碳纤维/ 环氧复合材料不同保温
时间下的固化度数据如表 2 所示ꎮ 由表 2 数据可
知:保温时间为 6 min~8 min 的层合板ꎬ固化度满足
要求ꎮ 但考虑到分层缠绕下复合材料需经过多次微
波辐射ꎬ由于热传导或弱微波等效应导致已缠绕层
固化度提高ꎬ因此保温时间暂定为 6 minꎮ
图 5 环氧树脂的黏度 ̄温度曲线
Fig? 5 Viscosity ̄temperature curve of epoxy resin
表 2 铺层方式为[90° 2
/ ±20°]的碳纤维/ 环氧
复合材料不同保温时间下的固化度
Table 2 Curing degree of carbon fiber/epoxy composite
with [90° 2
/ ±20°] laminating method
under different holding time
升温
制度
保温
时间
/ min
ΔH1
/ J?g
-1
ΔH2
-1
/ J?g
-1
ΔH2
-2
/ J?g
-1
ΔH2
-3
/ J?g
-1
ΔHavg
/ J?g
-1
α
/ %
离散
系数
/ %
5 ℃ / minꎬ
30 ℃ ~
90 ℃
0
2
4
6
8
10
117
63.70 55.20 57.29 58.73 49.8 7.5
45.80 55.72 64.50 55.34 52.7 16.9
46.81 50.44 45.61 47.62 59.3 5.3
33.97 29.31 34.64 32.64 72.1 8.9
19.75 25.34 29.31 24.80 78.8 19.4
24.69 19.82 20.77 21.76 81.4 11.9
微波预固化下ꎬ“表层” ([90°2
/ ±20°]) 对已缠
绕层存在热传导、弱微波等效应ꎬ试验研究该效应对
已缠绕层固化度的影响ꎬ具体实验方案如图 6 所示ꎮ
图 6 微波分层预固化试验示意图
Fig? 6 Schematic diagram of microwave layered pre ̄curing test
根据暂定的微波预固化工艺(表 3 中 1#工艺)ꎬ
考虑热传导、弱微波效应对复合材料固化度的影响ꎬ
设计了其他四种微波预固化工艺ꎬ具体工艺列于表
3ꎮ 各工艺下复合材料的固化度变化趋势如图 7 所
示ꎮ 随着微波预固化次数的增加ꎬ复合材料的固化
度逐渐增加ꎬ最终趋于稳定ꎬ可以认为复合材料的固
化度不再随着微波预固化次数而改变ꎮ 因此ꎬ4#分
层微波预固化工艺满足碳纤维/ 环氧复合材料整体
固化度为 70% ~80%的要求ꎮ
92 2021 年 12 月
???????????????????????????????????????????????


















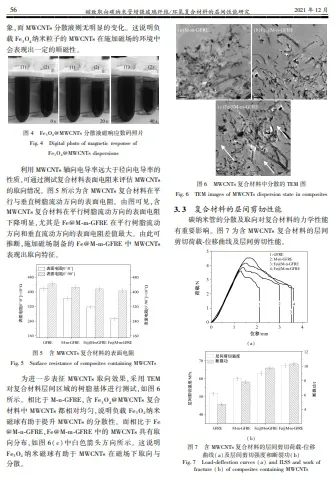

















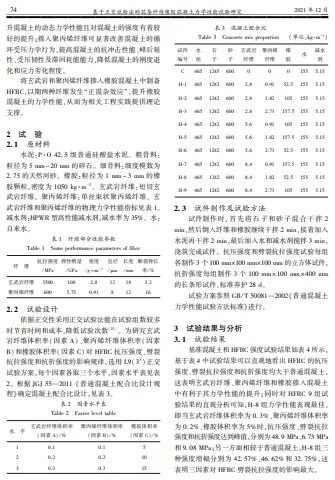

















 该页无缩略图
该页无缩略图



