李老师专用教案（精品原创） 微信：15192086110抖音：866460001

51 数学加分宝9 上《天天练》第6 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1．甲、乙两人玩“石头，剪刀，布”的游戏，约定只玩一局，描述错误的是（C ）A．甲，乙获胜的概率均低于 0.5 B．甲，乙获胜的概率相同

C．甲，乙获胜的概率均高于 0.5 D．游戏公平

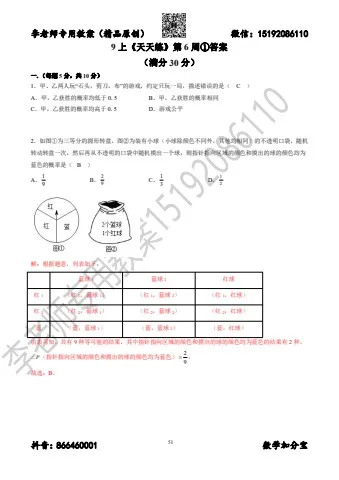
2．如图①为三等分的圆形转盘，图②为装有小球（小球除颜色不同外，其他均相同）的不透明口袋，随机转动转盘一次，然后再从不透明的口袋中随机摸出一个球，则指针指向区域的颜色和摸出的球的颜色均为蓝色的概率是（ B ）

A．

1

9

B．

2

9

C．

1

3

D．

1

2

解：根据题意，列表如下：

蓝球 1 蓝球 2 红球红 1 （红 1，蓝球 1） （红 1，蓝球 2） （红 1，红球）红 2 （红 2，蓝球 1） （红 2，蓝球 2） （红 2，红球）蓝 （蓝，蓝球 1） （蓝，蓝球 2） （蓝，红球）由表可知，共有 9 种等可能的结果，其中指针指向区域的颜色和摸出的球的颜色均为蓝色的结果有2种，P（指针指向区域的颜色和摸出的球的颜色均为蓝色）

2

9  ，

故选：B．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

52 数学加分宝二.（每题 5 分，共 10 分）

1．在一个不透明的盒子中装有 10 个白球，若干个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是白球的概率为

2

3 ，则黄球的个数为（ ）

A．4 B．5 C．6 D．7

解：设黄球的个数为 x 个，

根据题意得： 3

0

10

1 2

x =

+ ，

解得： x  5，

经检验，x=5 是所列方程的根且符合实际意义， 黄球的个数为 5．

故选：B．

2．关于 x 的一元二次方程 2 ax  bx 1  0中的常数 a 和 b 是  2，0，4 中的任意两个数，则该一元二次方程有解的概率为（ ）

A．

1

2

B．

1

3

C．

2

3

D．

1

4

解：关于 x 的一元二次方程 2 ax  bx 1  0有解，

∴a  0，且 

2 b  4a  0，

∴a  0，且 2 b  4a  0，

∵常数 a 和 b 是-2，0，4 中的任意两个数，

∴a 和 b 的值有以下几种情况：

①当a  2，b  0 时， 2 b  4a  0  4(2)  8  0，符合题意；

②当a  2，b  4 时， 2 b  4a 16  4(2)  24  0，符合题意；

③当a  0，b  2 时，该方程不是一元二次方程，不符合题意；

④当a  0，b  4 时，该方程不是一元二次方程，不符合题意；

⑤当a  4，b  2 时， 2 b  4a  4  44  12  0 ，不符合题意；

⑥当a  4，b  0 时， 2 b  4a  0  44  16  0 ，不符合题意；

综上所述，共有 6 种等可能的结果，其中，该一元二次方程有解的结果有 2 种，∴该一元二次方程有解的概率为

2 1

6 3  ．

故选 B．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

53 数学加分宝三.（本题满分 10 分）

共享经济已经进入人们的生活．小沈收集了自己感兴趣的 4 个共享经济领域的图标，共享出行、共享服务、共享物品、共享知识，制成编号为 A、B、C、D 的四张卡片（除字母和内容外，其余完全相同）．现将这四张卡片背面朝上，洗匀放好．

（1）小沈从中随机抽取一张卡片是“共享服务”的概率是 ；

（2）小沈从中随机抽取一张卡片（不放回），再从余下的卡片中随机抽取一张，请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率．（这四张卡片分别用它们的编号A、B、C、D 表示）

解：（1）∵有共享出行、共享服务、共享物品、共享知识，共四张卡片，

∴小沈从中随机抽取一张卡片是“共享服务”的概率是

1

4 ，

故答案为：

1

4 ；

（2）画树状图如图：

共有 12 种等可能的结果数，其中两张卡片恰好是“共享出行”和“共享知识”的结果数为2，∴抽到的两张卡片恰好是“共享出行”和“共享知识”的概率= 2 1

12 6  ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

54 数学加分宝9 上《天天练》第6 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1．一个不透明的袋子装有除颜色外其余均相同的 2 个白球和n 个黑球．随机地从袋中摸出一个球记录下颜色，再放回袋中摇匀．大量重复试验后，发现摸出白球的频率稳定在 0.2 附近，则n的值为（）A．2 B．4 C．8 D．10

解：依题意有：

2

2  n

=0.2，

解得：n=8．

故选：C．

2．取一根长为3米的绳子，拉直后在任意位置剪断，那么剪得两段的长都不少于1米的概率是（）A．

1

3

B．

1

2

C．

2

3

D．

3

4

解：记“剪得两段的长都不少于 1 米”为事件 A，

则只能在中间 1m 的绳子上剪断，剪得两段的长都不少于 1 米，

∴事件 A 发生的概率为 P（A）= 1

3 ；

故选：A．

二.（每题 5 分，共 10 分）

1.书架上有 3 本小说、2 本散文，从中随机抽取 2 本都是小说的概率是（ A ）A. 10

3

B. 25

6

C. 25

9

D. 5

3

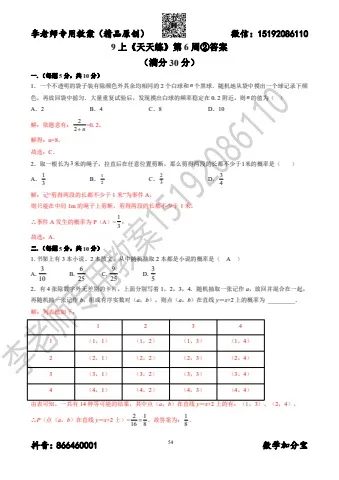
2．有 4 张除数字外无差别的卡片，上面分别写着 1，2，3，4．随机抽取一张记作a，放回并混合在一起，再随机抽一张记作 b，组成有序实数对（a，b），则点（a，b）在直线 y＝x+2 上的概率为_________．解：列表法如下：

1 2 3 4

1 （1，1） （1，2） （1，3） （1，4）2 （2，1） （2，2） （2，3） （2，4）3 （3，1） （3，2） （3，3） （3，4）4 （4，1） （4，2） （4，3） （4，4）由表可知，一共有 14 种等可能的结果，其中点（a，b）在直线 y＝x+2 上的有：（1，3）、（2，4），∴P（点（a，b）在直线 y＝x+2 上）= 2 1

16 8  ，故答案为：

1

8 ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

55 数学加分宝三.（本题满分 10 分）

2021 年 4 月，教育部印发《关于进一步加强中小学生睡眠管理工作的通知》，明确要求初中生每天睡眠时间应达到 9 小时．某初级中学为了解学生睡眠时间的情况，从本校学生中随机抽取100 名进行问卷调查，并将调查结果用统计图描述如下．

调查问卷

1．近两周你平均每天睡眠时间大约是______小时．

如果你平均每天睡眠时间不足 9 小时，请回答第 2 个问题

2．影响你睡眠时间的主要原因是______（单选）．

A．学习效率低 B．校外学习任务重

C．校内课业负担重 D．其他

平均每天睡眠时间 x（时）分为 5 组：①5  x  6；②6  x  7；③7  x 8 ；④8x9；⑤9x10．根据以上信息，解答下列问题：

（1）本次调查中，平均每天睡眠时间的中位数落在第_________（填序号）组；（2）随机调查一名学生，该学生睡眠时间达到 9 小时的概率是多少？

（3）若全校有 1000 名学生，请估计该校由于“学习效率低”而睡眠时间不足9 小时的人数；（4）请对该校学生睡眠时间的情况作出评价，并提出一条合理化建议．

(1)解：由于共有 100 人，因此中位数应为该组数据按从小到大或从大到小排列的第50 和51 个数据的平均数，由平均每天睡眠时间统计图可知，应位于第③组；故答案为：③．

(2)随机调查一名学生，该学生睡眠时间达到 9 小时的概率是

20 1

100 5 

(3)全校有 1000 名学生，请估计该校由于“学习效率低”而睡眠时间不足 9 小时的人数为：40%100080%  320（人）

(4)该校学生睡眠情况为：该校学生极少数达到《关于进一步加强中小学生睡眠管理工作的通知》中的初中生每天睡眠时间应达到 9 小时的要求，大部分学生睡眠时间都偏少，其中超过一半的学生睡眠时间达不到8 小时，约 4％的学生睡眠时间不到 6 小时．

建议：①减少校外学习任务时间，将其多出来的时间补充到学生睡眠中去；②减轻校内课业负担，提高学生的学习效率，规定每晚各科作业总时间不超过90 分钟等．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

56 数学加分宝9 上《天天练》第6 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1．如果任意选择一对有序整数（m，n），其中|m|≤1，|n|≤2，每一对这样的有序整数被选择的可能性是相等的，那么关于 x 的方程 x

2+nx+m＝0 有两个相等实数根的概率是_____．

解：∵|m|≤1，|n|≤2，

∴m＝0，±1，

n＝0，±1，±2，

∴有序整数（m，n）共有 3×5＝15（种），

∵方程 x

2+nx+m＝0 有两个相等实数根，

则需：△＝n

2﹣4m＝0，

有（0，0），（1，2），（1﹣2）三种可能，

∴关于 x 的方程 x

2+nx+m＝0 有两个相等实数根的概率是

3 1

15 5  ．

故答案为

1

5 ．

2．四张背面相同的扑克牌，分别为红桃 1、2、3、4，背面朝上，先从中抽取一张把抽到的点数记为a，不放回再另抽取一张点数记为 b，则点（a， b）在直 y＝x＋1 上的概率为________．解：画出树状图如图所示，

由树状图可知：一共有 12 种等可能的结果，其中点（a，b）在直线 y＝x＋1 上的有（1，2），（2，3），（3，4），3 种结果，

∴点（a，b）在直线 y＝x＋1 上的概率为

3 1 =

12 4 ，

故答案为：

1

4

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

57 数学加分宝二.（每题 5 分，共 10 分）

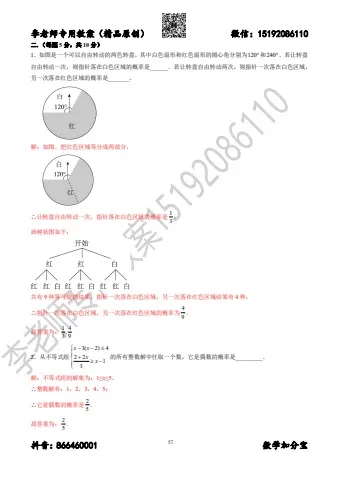
1．如图是一个可以自由转动的两色转盘，其中白色扇形和红色扇形的圆心角分别为120和240．若让转盘自由转动一次，则指针落在白色区域的概率是______．若让转盘自由转动两次，则指针一次落在白色区域，另一次落在红色区域的概率是_______．

解：如图，把红色区域等分成两部分，

∴让转盘自由转动一次，指针落在白色区域的概率是

1

3 ；

画树状图如下：

共有 9 种等可能的结果，指针一次落在白色区域，另一次落在红色区域结果有4 种，∴指针一次落在白色区域，另一次落在红色区域的概率为

4

9 ．

故答案为：

1 4

, 3 9

2．从不等式组

3( 2) 4

2 2

1

3

x x

x

x

   



 

  



的所有整数解中任取一个数，它是偶数的概率是_________．解：不等式组的解集为：1≤x≤5，

∴整数解有：1，2，3，4，5；

∴它是偶数的概率是

2

5 ．

故答案为：

2

5 ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

58 数学加分宝三.（本题满分 10 分）

【数学试验】

数学学习小组在学习“用频率估计概率”的数学活动课上，做投掷骰子（质地均匀的正方体)试验，他们共做了 100 次试验，试验的结果如下：

向上点数 1 2 3 4 5 6

出现次数 12 19 15 18 20 x

（1）求表格中 x 的值；

（2）计算“3 点朝上”的频率．

（3）【数学发现】数学学习小组针对数学试验的结果提出结论：“根据试验及‘用频率估计概率’的知识，出现 1 点朝上的概率是 12％．”你认为数学学习小组的结论正确吗？并说明理由．（4）【结论应用】在一个不透明的盒子里，装有 40 个黑球和若干个白球，它们除颜色外都相同，搅匀后从中任意摸出一个球，记下颜色再把它放回盒子中，不断重复试验，统计结果发现，随着试验次数越来越多，摸到黑球的频率逐渐稳定在 0.2 左右．据此估计盒子中大约有白球多少个？(1)解：由题意得： x  100 12 19 15 18  20  16 ；

(2)解：3 点朝上出现的次数是 15，

所以 3 点朝上出现的频率

15 3

100 20   ；

(3)答：数学学习小组的结论不正确，因为 1 点朝上的频率为12%，不能说明1 点朝上这一事件发生的概率就是12% ，只有当实验的次数足够多时，该事件发生的频率才稳定在事件发生的概率附近，才可以将这个频率的稳定值作为该事件发生的概率；

(4)解：设盒子中大约有白球 x 个，根据题意得：

40

0.2

40 x 

 ，

解得： x 160 ．

经检验 x 160 是原方程的解，

答：估计盒子中大约有白球 160 个．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

59 数学加分宝9 上《天天练》第6 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则这两个数的和是 2 的倍数或是 3 的倍数的概率等于 （ C ）

A．

16

3

B．

8

3

C．

8

5

D．16132.小彭同时投掷两枚普通的正方体骰子（骰子各个面分别标有点数1， 2 ，3 ，4，5，6），所得两个数字之和小于 4的概率是（ A ）

A. 1

12

B. 1

9

C. 1

6

D. 14二.（每题 5 分，共 10 分）

1. 在一个不透明的盒子里装着若干个白球，小明想估计其中的白球数，于是他放入10个黑球，搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，得到如下数据：摸球的次数 n 20 40 60 80 120160200摸到白球的次数 m 15 33 49 63 97128158摸到白球的频率 m

n

0.75 0.83 0.82 0.79 0.810.800.79估算盒子里白球的个数为（ ）

A. 8 个 B. 40 个 C. 80 个 D. 无法估计选 B．大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，观察可知概率在0.8 左右2.如图所示，一只蚂蚁从 A 点出发到 D，E，F 处寻觅食物．假定蚂蚁在每个岔路口都可能的随机选择一条向左下或右下的路径（比如 A 岔路口可以向左下到达 B 处，也可以向右下到达C 处，其中A，B，C都是岔路口）．那么，蚂蚁从 A 出发到达 E 处的概率是

2

1 ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

60 数学加分宝三.（本题满分 10 分）

某大学利用”世界献血日”，开展自愿义务献血活动．经过检测，献血者血型有：“A，B，AB，O”四种类型．随机抽取部分献血结果进行统计，根据结果制作了如下两幅不完整统计图表．血型统计表：

血型 A B AB O

人数 10 5

血型统计图：

（1）本次随机抽取献血者人数为____________人，图中 m＝____________；（2）补全表中的数据；

（3）若这次活动中该校有 1200 人义务献血，估计大约有多少人是 A 型血？（4）现有 4 个自愿献血者，2 人为 O 型，1 人为 A 型，1 人为 B 型，若在 4 人种随机挑选2 人，利用树状图或列表法求两人血型均为 O 型的概率．

解：(1)这次随机抽取的献血者人数为 5÷10%=50（人），所以 m= 10

50

×100=20；故答案为50，20；(2)O 型献血的人数为 46%×50=23（人），A 型献血的人数为 50-10-5-23=12（人），血型 A B AB O

人数 12 10 5 23

故答案为 12，23；

(3)从献血者人群中任抽取一人，其血型是 A 型的概率= 12 6 =

50 25 ，1200× 6

25

=288，估计这 1200 人中大约有 288 人是 A 型血；

(4)画树状图如下

由树状图可以看出，所有可能出现的结果共有 12 种，这些结果出现的可能性相同．其中两人都为O型的有2 种．∴P（两人均为 O 型）＝

2

12 ＝

1

6

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

61 数学加分宝9 上《天天练》第6 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1.为了估算湖里有多少条鱼，从湖里捕上 100 条做上标记，然后放回湖里，经过一段时间待标记的鱼全混合于鱼群中后，第二次捕得 200 条，发现其中带标记的鱼 25 条，我们可以估算湖里有鱼___________条．【详解】设鱼塘里约有鱼 x 条，

依题意得 200：25=x：100，

∴x=800，

∴估计鱼塘里约有鱼 800 条．

故答案为：800

2.下列说法正确的是（ B ）

①试验条件不会影响某事件出现的频率

②在相同的条件下试验次数越多，就越有可能得到较好的概率值，但各人所得的值不一定相同③如果一枚骰子的质量分布均匀，那么抛掷后每个点数出现的概率均等

④抛掷两枚质量分布均匀的相同的硬币，出现“两个正面”“两个反面”“一正一反”的概率相同网ZXXK]

A.①② B.②③ C.③④ D.①③二.（每题 5 分，共 10 分）

1.用图中两个可自由转动的转盘做“配紫色”游戏：分别旋转两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色．那么可配成紫色的概率是（ D ）

A．

4

1

B．

4

3

C．

3

1

D．212.在一个不透明的袋子中装有除颜色外其余均相同的 8 个小球，其中红球 3 个，黑球5 个.若再放入m个一样的黑球并摇匀，此时，随机摸出一个球是黑球的概率等于 0.8，则 m的值为7 .

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

62 数学加分宝三.（本题满分 10 分）

为了弘扬美食文化，助力黔菜出山，某数学兴趣小组在国际广场展开了“舌尖上的贵阳一我最喜爱的贵阳小吃”的随机调查，并给出四种选择（A．丝娃娃，B．肠旺面，C．老素粉，D．豆腐果），每人选且只选一种，该兴趣小组将调查得到的数据整理后，绘制成如下两幅不完整的统计图．根据以上信息，解答下列问题：

（1）本次共调查了___________人，请补全条形统计图；

（2）已知西秀区人口约 87 万人，估计西秀区市民中最喜欢老素粉的有________万人；（3）“五·一”小长假期间，小度打算去贵阳旅游，并从以上四种小吃中随机选择两种不同的小吃进行品尝，请用列表或画树状图的方法求小度选中肠旺面和豆腐果的概率．

(1)解：调查的总人数为21 42%  50 （人），

故答案为：50；

喜欢 C 的人数为 50-13-21-4=12（人），

补全统计图：

(2)西秀区市民中最喜欢老素粉的有

12

87 20.88

50

  （万人），

故答案为：20.88；

(3)树状图如下，

共有 12 种等可能的情况，其中选中肠旺面和豆腐果的结果有 2 种，

∴P（选中肠旺面和豆腐果）= 2 1

12 6  ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

63 数学加分宝9 上《天天练》第7 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.若 y  2x  0，则 x：y 等于（ ）

A．1：2 B．1：4 C．2：1 D．4：1

【答案】A

2．已知

3

5

a

b  ，则

a b

b a





的值为（ ）

A．2 B．

5

2

C．4 D．

4

5

【答案】C 解：∵

3

5

a

b  ，∴设 a=3k，b=5k，∴

3 5 8

5 3 2

a b k k k

b a k k k

 

 

 

=4，故选：C．二.（每题 5 分，共 10 分）

1．已知

6

7

x

y  ，则下列结论一定成立的是（ ）

A．x＝6，y＝7 B．

13

7

x y

y



 C． y  x 1 D． 7 6x y 【答案】B

2．下列各组线段中，不成比例的是（ ）

A．30cm,20cm,90cm,60cm B．4cm,6cm,8cm,10cmC．11cm,22cm,33cm,66cm D．2cm,4cm,4cm,8cm【答案】B

三.（每题 5 分，共 10 分）

1．若

2

3

y

x  ，则

x y

x



 ________．

【答案】

5

3

【详解】解：

2

3

y

x  ，设x  3k， y  2k (k  0) ，3 2 5

3 3

x y k k

x k

 

  ．故答案为：53．2．若 2

a c

b d    ，则

a c

b d



＝（ ）

A．2 B．2 C．

1

2  D．

1

2

【答案】A

【详解】解： 2

a c

b d

    ，∴a＝﹣2b，c＝﹣2d，

2 2 2( ) 2( )

a c b d b db d b d b d        ．故选：A．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

64 数学加分宝9 上《天天练》第7 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1．如果

a c e

k

b d f    （b+d+f≠0），且 a+c+e＝5（b+d+f）．则 k= ．【答案】5

2．若

3

4

a c e

b d f    ，则

2 3

2 3

a c e b d f  



 

________．

【答案】

3

4

∵

3

4

a c e

b d f    ∴

3 3 3

4 4

, , 4

a  b c  d e  f ∴

3 3 3

2 3

2 3 32334 4 4

2 3 2 3 4234b d f a c e bdf

b d f b d f bdf    

       ．二.（每题 5 分，共 10 分）

1．已知 0

2 3 4

a b c    ，且a  b  c  4 ，则a  ______．

【答案】8

【详解】解：设 =

2 3 4

a b c   k ，则a  2k,b  3k, c  3k ，∴a  b  c  2k  3k 4k 4，∴k  4，∴a  2k  2 4  8，故答案为：8．

2．若 0

5 7 8   

a b c ，且3a  2b  c  3，则 a b c 的值是（ A ）

A．

3

4

B.4 C.14 D.42

三.（本题满分 10 分）

已知 a：b＝3：2，求：

（1）

a b

b

 （2）

2 7

4

a b

b

【答案】(1) 5

2

(2)-1

解：∵a：b＝3：2，∴设 a＝3k，b＝2k（k≠0），

3 2 5

2 2

a b k k

b k

 

  ；

（2）解：∵a：b＝3：2，∴设 a＝3k，b＝2k（k≠0），

2 7 2 3 7 2

1

4 4 2

a b k k

b k    

  



．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

65 数学加分宝9 上《天天练》第7 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1．如图，直线 l1∥l2∥l3，直线 a，b 分别与这三条平行线相交，交点分别为点A，B，C 与点D，E，F．已知

2

3  AB

BC

，EF＝9，则 DE 的长为（ ）

A．3 B．6 C．13.5 D．19.5

【答案】B

2．如图 1 2 3

l ∥l ∥l ，直线 AC 与 DF 交于点 O，且与 1

l ， 2

l ， 3

l 分别交于点 A，B，C，D，E，F，则下列比例式不正确的是（ ）

A． AB DE

BC EF

 B． AB DE

BO EO

 C． OB OE

OC OF

 D． ADAOCFAC【答案】D

二.（每题 5 分，共 10 分）

1．如图，在△ABC 中，DE∥BC，AE＝4，EC＝6，AB＝5，则 BD 的长为（）A．1 B．2 C．3 D．4

【答案】C

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

66 数学加分宝2．如图，在△ABC 中，点 D，E，F 分别在 AB，AC，BC 边上，DE∥BC，EF∥AB，则下列结论正确的是（ ）

A． AD AE

DB AC

 B． AD BF

DB FC

 C． AD FC

DB BF

 D． ADFCDBBC【答案】B

三.（本题满分 10 分）

如图，△ABC 中，DE∥BC，EF∥AB，AE＝2CE，AB＝12，BC＝18，求四边形BDEF 的周长．【答案】32

【分析】由题中条件可得四边形 DBFE 是平行四边形，再由平行线分线段成比例的性质球的线段BD、DE的长，进而即可求解其周长．

【详解】解：∵DE∥BC，EF∥AB，

∴四边形 DBFE 是平行四边形，

∴EF=BD，DE=BF，

∵DE∥BC，

∴ AE AD DE

AC AB BC

   ，

∵AE=2CE，

∴

2

3 12 18

AE AD DE

AC

   ，

∴DE=12，AD=8，即 BD=4，

∴四边形 BDEF 的周长=2（BD+DE）=2×（4+12）=32．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

67 数学加分宝9 上《天天练》第7 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1．如图，AB∥CD∥EF，有 BF=3DF，则 AC

CE

的值是_____________．

【答案】2

2．如图： AB∥CD∥EF ， AD : DF  3:1, BE 12，那么 CE 的长为（ ）A．3 B．4 C．5 D．6

【答案】A

二.（每题 5 分，共 10 分）

1．如图，已知在△ABC 中，点 D、E、F 分别是边 AB、AC、BC 上的点，DE∥BC,EF∥AB，且AD:DB3:5，那么 CF

CB

等于___________．

【答案】

5

8

2．如图，已知在△ABC 中，DE∥BC，EF∥AB，AE=2CE，AB=6，BC=9，那么四边形BDEF 的周长是_________．【答案】16

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

68 数学加分宝三.（本题满分 10 分）

如图，在△ABC 中，DE∥BC，EF∥CD．

（1）求证：AF：FD＝AD：DB；

（2）若 AB＝30，AD：BD＝2：1，请直接写出 DF 的长．

【答案】（1）见详解；（2）

20

3 ．

【分析】（1）利用平行线分线段成比例定理，由 EF∥CD 得到 AF：FD=AE：EC，由DE∥BC得到AE：EC=AD：DB，再进行等量代换即可求解；

（2）根据比例的性质得到 AD  20，根据（1）结论得到 AF：FD=2:1，即可求出DF．【详解】解：（1）证明：∵EF∥CD，

∴AF：FD=AE：EC，

∵DE∥BC，

∴AE：EC=AD：DB，

∴AF：FD＝AD：DB；

（2）∵AB＝30，AD：BD＝2：1，

∴

2 2

30 20

3 3

AD  AB    ，

∵AF：FD＝AD：DB，

∴AF：FD=2:1，

∴

1 1 20

20

3 3 3

DF  AD    

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

69 数学加分宝9 上《天天练》第7 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1．如图，已知 AB∥CD∥EF，AD：AF=3：5，BC=6，则 CE 的长为_________．【答案】4

2．如图，已知 AB  CD  EF ，它们依次交直线 1

l ， 2

l 于点 A，D，F 和点 B，C，E，如果AD＝6，DF＝3，BC＝5，那么 BE＝__________．

【答案】7.5

二.（每题 5 分，共 10 分）

1．下面一定相似的一组图形为（ ）

A．两个等腰三角形 B．两个矩形 C．两个等边三角形 D．两个菱形．【答案】C

2．国旗法规定：所有国旗均为相似矩形，在下列四面国旗中，其中只有一面不符合标准，这面国旗是（）A． B．

C． D．

【答案】B

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

70 数学加分宝三.（每题 5 分，共 10 分）

1．将一张长方形纸片对折，若得到的小长方形与原长方形相似，则原长方形的长与宽的比是________．【答案】 2 ∶1

【分析】设 AE＝ED＝a，AB＝b，根据每一个小长方形与原长方形相似，可知2abba，再由a，b均为正数可知 b＝ 2 a，由此即可得出结论．

【详解】解：设 AE＝ED＝a，AB＝b，

∵每一个小长方形与原长方形相似，

∴

2

a b

b a  ，

∴b

2＝2a

2，

∵a，b 均为正数，

∴b＝ 2 a，

∴

2 2

2

2

AD a a

AB b a    ，

∴原长方形的长与宽之比为 2 ：1．

故答案为： 2 ：1．

2．如图，一个矩形广场的长为 90m，宽为 60m，广场内有两横，两纵四条小路，且小路内外边缘所围成的两个矩形相似，如果两条横向小路的宽均为 1.2m，那么每条纵向小路的宽为m．【答案】1.8

【分析】根据两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形列出比例式解答即可．

【详解】解：设每条纵向小路的宽为 xm，则小路内缘所围成的矩形的长为（90-2x）m，宽为（60-2.4）m，∵小路内外边缘所围成的两个矩形相似，

∴

90 2 60 2.4

90 60  x 

 ，

解得，x＝1.8，

故答案为：1.8

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

71 数学加分宝9 上《天天练》第8 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.（李沧期中）若3x  5y 则

y

x

=___ 3

5

___ .

2.（市北期中）已知 ( 0 0) 2 3  a  b 

a b ， ，则下列变形正确的有（ C ）个. （1）

3

2 

b

a （2） 2a  3b （3）

2

3 

a

b （4）3a  2b

A．1 B.2 C.3 D.4

二.（每题 5 分，共 10 分）

1.（市北期中）如果

7

9

a c

b d   ,那么

2 3

2 3

a c

b d 



=___ 7

9

___.

2.（市南期中）如图，已知 AB //CD // EF ，那么下列结论正确的是（ A ）A. CE

BC

DF

AD

 .B. AD

DF

CE

BC

 C. BE

BC

EF

CD

 .D. AFADEFCD三.（每题 5 分，共 10 分）

1.（全市期中统考）如图，直线 a∥b∥c ，直线 AC 与 DF 交于点O，且与直线a，b，c分别交于点A，B，C，D，E，F ，如果 DE  2，EF  5，AC  6，那么 AB 的长为___ 12

7

_______.第 1 题图 第 2 题图

2.（市南期中）如图，在△ABC 中， D、E 分别为 AB、AC 边上的点， DE∥BC, BE与CD相交于点F ，则下列结论一定正确的是（ A ）

A. AC

AE

FC

DF

 B. AC

EC

AB

AD

 C. BC

DE

DB

AD

 D. FCEFBFDF

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

72 数学加分宝9 上《天天练》第8 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1.（市南期中）如图，在△ABC 中，点 D 在 BC 边上，连接 AD，点 G 在线段AD 上，GE∥BD，且交AB于点 E，GF∥AC，且交 CD 于点 F，则下列结论一定正确的是（ D ）

A. AD

AG

AE

AB

 B. AD

DG

CF

DF

 C. BD

EG

AC

FG

 D. DFCFBEAE2.（李沧期中）如图，在△ABC 中，点 E 在 BC 边上，连接 AE，点 D 在线段AE 上，GD∥BA，且交BC于点 G，DF∥BC，且交 AC 于点 F，则下列结论一定正确的是（ D ）

A. BE

BG

DE

AD

 B. CE

DF

DE

AD

 C. AF

CF

AB

DG

 D. BEBGACAF二.（每题 5 分，共 10 分）

1.（市北期中）如图，在△ABC中，DE//BC，AD=2，AE=3，BD=4，则AC的长为（A）A.9 B.8 C.7 D.6

2.（局属期中）如图，在 ABC 中， DE // BC ， BD  3AD， BC12 ，则DE的长是（A）A.3 B.4 C.5 D.6

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

73 数学加分宝三.（本题满分 10 分）

如图，一个矩形广场的长 AB 120米，宽 AD  60 米，广场内两条纵向的小路宽为a 米，横向的两条小路宽为 b 米，矩形 ABCD  矩形 EFGH．

（1）求a :b 的值；

（2）若a  4 ，求矩形 EFGH 的面积．

（1）根据题意可知：HE＝（60﹣2b）米，EF＝（120﹣2a）米，

∵矩形 ABCD∽矩形 EFGH．

∴ HE EF

AD AB

 ，∴

60 2 120 2

60 120  b  a  ，

整理，得 2b＝a，

∴a：b＝2：1；

（2）∵a＝4，2b＝a，∴b＝2，

∴矩形 EFGH 的面积＝EF•HE＝（120﹣2a）•（60﹣2b）＝（120﹣8）（60﹣4）＝112×56＝6272（米2）．答：矩形 EFGH 的面积为 6272 米 2．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

74 数学加分宝9 上《天天练》第8 周③答案（满分30 分）一.（每题 5 分，共 10 分）

1.（市南期中）如图，点 D ，E 分别在 AB ，AC 上，且ABC  AED.若DE4，AE5, BC8，则 AB 的长为 10 .

2.如图，具备下列条件①1 C ，②A  C ，③2  B ，④ ADAEACAB 之一，就可以判定AED与ABC 相似的是（ ）

A．①②③ B．②③④ C．①②④ D．①③④【答案】D

二.（每题 5 分，共 10 分）

1.如图，在 ABC 中，P、Q 分别为 AB、AC 边上的点，且满足 AP AQACAB ．根据以上信息，嘉嘉和淇淇给出了下列结论：

嘉嘉说：连接 PQ，则 PQ//BC．

淇淇说： AQP ∽ ABC ．

对于嘉嘉和淇淇的结论，下列判断正确的是（ ）

A．嘉嘉正确，淇淇错误 B．嘉嘉错误，淇淇正确 C．两人都正确D．两人都错误【答案】B

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

75 数学加分宝2.如图，如果∠BAD＝∠CAE，那么添加下列一个条件后，仍不能确定△ADE 与△ABC 相似的是（）A．B＝∠D B．∠C＝∠AED C． AB

AD

＝ DE

BC

D． ABAD＝ACAE【答案】C

三.（每题 5 分，共 10 分）

1.如图，在 ABC 中， AB  8cm， BC 16cm ，动点 P 从点 A 开始沿 AB 边运动，速度为2cm/ s；动点Q从点 B 开始沿 BC 边运动，速度为4cm / s ；如果 P、Q 两动点同时运动，那么经过______秒时△QBP与ABC相似．

【答案】0.8或2

2.在 RtABC 和 Rt△DEF 中，C  F  90， AC  3， BC  4， DF6，DE8，判定这两个三角形是否相似．

【答案】不相似

【分析】求出 2 2 EF  8  6  2 7 ，利用

3 6

4 2 7    AC DF

BC EF

，即可求出两个三角形不相似．【详解】解：∵F  90 ， DF  6， DE  8 ，

∴ 2 2 EF  8  6  2 7 ，

∵C  F  90， AC  3， BC  4，

∴

3 6

4 2 7    AC DF

BC EF

，

∴这两个三角形不相似．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

76 数学加分宝9 上《天天练》第8 周④答案（满分30 分）一.（每题 5 分，共 10 分）

1.在△ABC 和△DEF 中，AB=6，BC=8，DE=4，∠B=∠E，当 EF=_________时，△ABC 与△DEF相似.【答案】

16

3 或 3

2.如图所示，网格中相似的两个三角形是（ ）

A．①与② B．①与③ C．③与④ D．②与③【答案】B

二.（每题 5 分，共 10 分）

1.如图，在矩形 ABCD 中，点 E 是 BC 的中点，EF⊥AE 交 CD 于 F. （1）求证： ABE ∽ECF ；

（2）若 AB  3 ， BC  8，求 EF 的长. 【答案】（1）略（2）EF= 20

3

2.如图，四边形 ABCD、CDEF、EFGH 都是正方形.

(1)△ ACF 与△ ACG 相似吗?说说你的理由.

(2)求∠1+∠2 的度数. 【答案】（1）△ACF ∽△ACG 一角相等且组成角的两边成比例的两个三角形相似. （2）45

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

77 数学加分宝三.（每题 5 分，共 10 分）

1.如图，梯形 ABCD 中， AB //CD ，且 AB  2CD ， E 、 F 分别是 AB、BC的中点，EF与BD相交于点 M . （1）求证： EDM ∽FBM ； （2）若 DB  9 ，求 BM长度. 【答案】（1）证 DE//BC 可得 EDM ∽FBM （2）3

2.如图，在正方形 ABCD 中，E，F 分别是边 AD， CD 上的点，AE=ED，DF= 4

1

DC，连接EF并延长，交BC 的延长线于点 G. （1）求证： ∆ABE∽∆DEF；

（2）若正方形的边长为 4，求 BG 的长.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

78 数学加分宝9 上《天天练》第8 周⑤答案（满分30 分）一.（每题 5 分，共 10 分）

1.（市南期中）已知点 C 是线段 AB 的黄金分割点（AC>BC），AC=4，则线段AB 的长为（B）A. 2 5 - 2 B. 2 5  2 C. 6 - 2 5 D. 6 2 52.（市北期中）一个主持人站在舞台的黄金分割点处最自然得体，如果舞台AB长为20 米，一个主持人现在站在 A处，则他应至少再走（3010 5）米才最理想.二.（每题 5 分，共 10 分）

1.（局属期中）若点C 是线段 AB 的黄金分割点（ AC＞BC ）， AB 8cm，则BC(1245)cm2.（市北期中）主持人站在舞台的黄金分割点处最自然得体,如果舞台 AB 长为20 米,一个主持人现站在舞台AB 的黄金分割点点C 处,则下列结论一定正确的是（D ）

① AB : AC  AC : BC ; ② AC  6.18 米;

③ AC 10( 5 1) 米; ④ BC 10(3 5)米或10( 5 1) 米

A.①②③④ B.①②③ C.①③ D.④

三.（本题满分 10 分）

如图，乐器上的一根弦 AB = 80 cm ，两个端点 A.B 固定在乐器板面上，支撑点C 是靠近点B的黄金分割点，支撑点 D 是靠近点 A 的黄金分割点，求 C，D 之间的距离. 【答案】 AC  BD  40 5 1， BC 120  40 5 ， DC  BD  BC  80 5 160 cm

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

79 数学加分宝9上《天天练》第9周①答案（满分30分）一.（每题5分，共10分）

1．如图，C 为线段 AB 的黄金分割点（AC＜BC），且 BC＝2，则 AB 的长为（C ）A．2 5 ＋2 B．2 5 ﹣2 C． 5 ＋1 D． 5 ﹣3

2．已知线段 AB 的长为2厘米，点 P 是 AB 的黄金分割点，线段 PB 的长是（B ）A．

5 1

2

B． 5 1或3 5 C．3 5 D．51二.（每题5分，共10分）

1.若点C 为线段 AB 的黄金分割点，且 AC  BC ，则下列各式中不正确的是（C ）．A． AB : AC  AC : BC B．

3 5

2

BC AB





C．

5 1

2

AC AB



 D． AC  0.618AB

2.如图，线段 AB  1，点 P1是线段 AB 的黄金分割点(且 AP1  BP1

)，点 P2是线段AP1的黄金分割点（AP2P1P2），点 P3是线段 AP3 的黄金分割点 AP3  P2P3 ,, 依此类推，则线段 AP2020 的长度是（C ）A．

2020 5 1

2

  

 

 

B．

2021 5 1

2

  

 

 

C．

2020 3 5

2

  

 

 

D．2021 352 

 

 

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

80 数学加分宝三.（本题满分10分）

所谓黄金分割，指的是把长为 L 的线段分为两部分，使其中较长部分对于全部之比，等于较短部分对于该部分之比，其比值是

5 1

2

．

（1）如图①，在ABC 中，∠A＝36°， AB  AC ，∠ACB 的平分线 CD 交腰AB 于点D．请你根据所学知识证明：点 D 为腰 AB 的黄金分割点：

（2）如图②，在Rt△ABC 中，∠ACB＝90°，CD 为斜边 AB 上的高， ADBD，AB51，若点D是AB 的黄金分割点，求 BC 的长，

(1)证明：∵在ABC 中，∠A＝36°， AB  AC ，

∴

180

72

2

A

B ACB

 

     ．

∵CD 为∠ACB 的平分线，

∴

1

36

2

ACD = BCD  ACB = ，

∴∠ACD=∠BCD=∠A．

∴AD=DC．

∴BDC 180 B BCD  72．

∴∠BDC=∠B，∠BDC>∠BCD．

∴DC=BC，BC>BD．

∴BC=AD．

∴AD>BD．

∵CBD  ABC ，

∴△CBD∽△ABC ．

∴ BC BD

BA BC

 ，即 AD BD

BA AD

 ．

∴点 D 是腰 AB 的黄金分割点．

(2)解：∵点 D 是 AB 的黄金分割点，ADBD，∴

5 1

2

ADBDAB AD  ．∵ AB  5 1，

∴ AD 2 ．

∴ BD 5 1．

∵ACB  90，CD 是△ABC 斜边上的高，∴ACB  CDB90．∵ABC  CBD，

∴△ACB ∽△CDB．∴ AB BCCB BD ．

∴ 2 BC  AB  BD 5 1514．∴ BC  2．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

81 数学加分宝9上《天天练》第9周②答案（满分30分）一.（每题5分，共10分）

1.在上完相似三角形一课后，小方设计了一个实验来测量学校教学楼的高度．如图，在距离教学楼MN为18米的点 B 处竖立一个长度为2.8米的直杆，小方调整自己的位置，使得他直立时眼睛所在位置点C、直杆顶点 A 和教学楼顶点 M 三点共线．测得人与直杆的距离 DB 为2米，人眼高度CD 为1.6米，则教学楼的高度 MN 为（ C ）米．

A．12 B．12.4 C．13.6 D．15.2

2.如图，在某一时刻测得1米长的竹竿竖直放置时影长1.2米，在同一时刻旗杆AB 的影长不全落在水平地面上，有一部分落在楼房的墙上，他测得落在地面上影长为 BD＝9.6米，留在墙上的影长CD＝2米，则旗杆的高度（ C ）

A．9米 B．9.6米 C．10米 D．10.2米二.（每题5分，共10分）

1.我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？”其大意是：如图，一座正方形城池，A 为北门中点从点A往正北方向走30步到 B 处有一树木，C 为西门中点，从点 C 往正西方向走750步到D 处正好看到B 处的树木，则正方形城池的边长为（D ）步．

A．100 B．150 C．200 D．300

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

82 数学加分宝2.如图，有一块直角边 AB＝4cm，BC＝3cm 的 Rt△ABC 的铁片，现要把它加工成一个正方形（加工中的损耗忽略不计），则正方形的边长为（ D ）

A．

7

6

B．

37

30

C．

7

12

D．

37

60

三.（本题满分10分）

小明对某塔进行了测量，测量方法如下，如图所示，先在点 A 处放一平面镜，从A 处沿NA 方向后退1米到点 B 处，恰好在平面镜中看到塔的顶部点 M，再将平面镜沿 NA 方向继续向后移动15米放在D处（即AD＝15米），从点 D 处向后退1.6米，到达点 E 处，恰好再次在平面镜中看到塔的顶部点M、已知小明眼睛到地面的距离 CB＝EF＝1.74米，请根据题中提供的相关信息，求出小雁塔的高度MN（平面镜大小忽略不计）

解：根据题意得∠BAC＝∠NAM，∠ABC＝∠MNA，

∴Rt△AMN∽Rt△ACB，

∴ ，即 ①；

∵∠EDF＝∠NDM，∠DEF＝∠MND，

∴Rt△MND∽Rt△FED，

∴ ，即 ②，

由①②得 ，

解得 AN＝25，

∴ ，

解得 MN＝43.5，

答：小雁塔的高度 MN 为43.5米．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

83 数学加分宝9上《天天练》第9周③答案（满分30分）一.（每题5分，共10分）

1.在小孔成像问题中，根据如图所示，若 O 到 AB 的距离是18 cm，O 到 CD 的距离是6 cm，则像CD的长是物体 AB 长的（ C ）

A．3倍 B．

1

2

C．

1

3

D．2倍2.如图，在△ABC 中，DE BC， AD  9 ， DB  3， DE=6 ，则 BC 的长为（C ）A．6 B．7 C．8 D．9

二.（每题5分，共10分）

1.在RtABC 中，C=90，四边形CDEF 为内接正方形．若 AE  10cm， BE 5cm，则阴影部分的面积是（ C ） 2 cm ．

A．24 B．30 C．25 D．10 5

2.如图，在等边△ABC 中，点 D、E 分别在边 BC、AC 上，且ADE  60，BD=1，23CE，则△ABC的面积为（ C ）

A．3 B．9 C．

9 3

4

D．

9 3

2

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

84 数学加分宝三.（本题满分10分）

如图，直线

3 = +6

4

y  x 与 x 轴交于 A 点，与 y 轴交于 B 点，动点 P 从 A 点出发，沿AO方向向点O匀速运动，同时动点Q 从 B 点出发，沿 BA 方向向点 A 匀速运动，P、Q 两点的运动速度都是每秒1个单位，当一个点停止运动，另一个点也随之停止运动，连接 PQ，设运动时间为ts0<t  8．问：当t 为何值时，以点 A、P、Q 为项点三角形与△ABO相似．

当

40

9

t  s 或

50

9

t  s 时，以点 A、P、Q 为项点三角形与△ABO相似

解：若以点 A、P、Q 为项点三角形与△ABO 相似，

则在△APQ 中， 或 ，

由题意可知，点 A 的坐标为（8，0），点 B 的坐标为（0,6），

∴OA=8，OB=6，AB=10，

∵运动时间为ts0  t  8 ，

∴AP=BQ=t，

则 AQ=10-t，

①当 时， △ABO AQP，

则 AP AO

AQ AB

 ，

∴

8

10 10

t

t 



，

解得：

40

9

t  （符合题意）；

②当 ， △ABO APQ，

则 AP AB

AQ AO

 ，∴

10

10 8

t

t 



，

解得：

50

9

t  （符合题意），

综上所述，当

40

9

t  s 或

50

9

t  s 时，以点 A、P、Q 为项点三角形与△ABO相似．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

85 数学加分宝9上《天天练》第9周④答案（满分30分）一.（每题5分，共10分）

1.如图，D 是△ABC 的边上的一点，过点 D 作 BC 的平行线交 AC于点 E，连接BE，过点D作BE的平行线交 AC 于点 F，则下列结论错误的是（ D ）

A． AD AF

BD EF

 B． AF DF

AE EB

 C． = AD AE

AB AC

D． CAFFEDEB2.如图，在△ABC 中，AH⊥BC 于 H，BC＝12，AH＝8，D、E 分别为 AB、AC 上的点，G、F是BC上的两点，四边形 DEFG 是正方形，正方形的边长 DE 为（ A ）

A．4.8 B．4 C．6.4 D．6

二.（每题5分，共10分）

1.如图，在ABCD 中，点 E 为 AD 的中点，点 F 为边 AB 上一点，且 AF: BF2: 3，连接CF，BE，相交于点 G，则 BG :GE （ A ）

A．6:7 B．7:6 C．3:4 D．4:5

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

86 数学加分宝2.如图，在ABCD 中，对角线 AC 与 BD 相交于点O，在 DC 的延长线上取一点E，连接OE交BC于点F，已知 AB=4 ， BC=6 ，CE  2，则CF 的长等于（ B ）

A．1 B．1.5 C．2 D．3

三.（本题满分10分）

在 Rt△ABC 中，∠C＝90°，AC＝20cm，BC＝15cm，现有动点 P 从点 A 出发，沿AC 向点C方向运动，动点 Q 从点 C 出发，沿线段 CB 也向点 B 方向运动，如果点 P 的速度是4cm/s，点Q 的速度是2cm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为 t 秒．求：（1）当 t＝3时，这时，P，Q 两点之间的距离是多少？

（2）若△CPQ 的面积为 S，求 S 关于 t 的函数关系式．

（3）当 t 为多少时，以点 C，P，Q 为顶点的三角形与△ABC 相似？

解：由题意得 AP＝4t，CQ＝2t，则 CP＝20﹣4t，

（1）当 t＝3时，CP＝20﹣4t＝8cm，CQ＝2t＝6cm，

由勾股定理得 PQ＝ ；

（2）由题意得 AP＝4t，CQ＝2t，则 CP＝20﹣4t，

因此 Rt△CPQ 的面积为 S＝ cm2；

（3）分两种情况：

①当 Rt△CPQ∽Rt△CAB 时， ，即 ，解得 t＝3；

②当 Rt△CPQ∽Rt△CBA 时， ，即 ，解得 t＝ ．因此 t＝3或 t＝ 时，以点 C、P、Q 为顶点的三角形与△ABC 相似．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

87 数学加分宝9上《天天练》第9周⑤答案（满分30分）一.（每题5分，共10分）

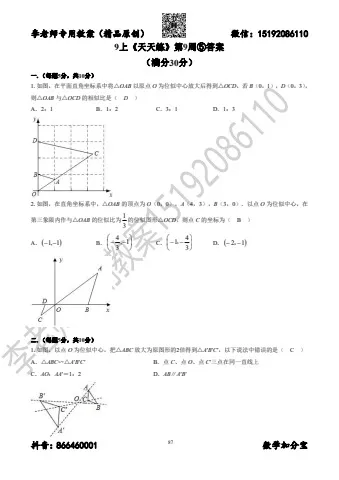
1.如图，在平面直角坐标系中将△OAB 以原点 O 为位似中心放大后得到△OCD，若B（0，1），D（0，3），则△OAB 与△OCD 的相似比是（ D ）

A．2：1 B．1：2 C．3：1 D．1：3

2.如图，在直角坐标系中，△OAB 的顶点为 O（0，0），A（4，3），B（3，0）．以点O为位似中心，在第三象限内作与△OAB 的位似比为

3

1 的位似图形△OCD，则点 C 的坐标为（B ）A．1,1 B． 









 ,1

3

4

C． 









 

3

4

1，D．2，1二.（每题5分，共10分）

1.如图，以点 O 为位似中心，把△ABC 放大为原图形的2倍得到△A′B′C′，以下说法中错误的是（C）A．△ABC∽△A′B′C′ B．点 C、点 O、点 C′三点在同一直线上C．AO：AA′＝1：2 D．AB∥A′B′

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

88 数学加分宝2.如图，线段 CD 两个端点的坐标分别为 C（﹣1，﹣2），D（﹣2，﹣1），以原点O 为位似中心，在第一象限内将线段 CD 扩大为原来的2倍，得到线段 AB，则线段 AB 的中点 E 的坐标为（A）A．3,3 B． 











2

3

2

3， C．2,4 D．4,2

三.（本题满分10分）

如图，在平面直角坐标系中，△ABC 的三个顶点的坐标分别为 A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长为1个单位长度）．

（1）画出△ABC 向下平移4个单位长度得到的△A1B1C1，点 C1的坐标是 ；（2）以点 B 为位似中心，在网格中画出△A2BC2，使△A2BC2与△ABC 位似，且位似比为2：1；（3）求出△A2BC2的面积．

解：（1）如图所示，△A1B1C1即为所求．点 C1的坐标为（2，﹣2）．故答案为：（2，﹣2）．（2）如图所示，△A2BC2即为所求．

（3） ＝ ＝ ×5×2+ ×5×2＝10．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

89 数学加分宝9上《天天练》第10周①答案（满分30分）一.（每题5分，共10分）

1．中心投影的投影线（ ）

A．相互平行 B．交于一点 C．相互垂直 D．在同一平面内【答案】B

2．下列结论正确的有（ ）

①同一时刻，同一公园内的物体在阳光照射下，影子的方向是相同的

②物体在任何光线照射下影子的方向都是相同的

③物体在路灯照射下，影子的方向与路灯的位置有关

④物体在点光源照射下，影子的长短仅与物体的长短有关

A．1 个 B．2 个 C．3 个 D．4 个【答案】B ①③正确

二.（每题5分，共10分）

1.如图是两根木杆及其影子的图形．

（1）这个图形反映的是中心投影还是平行投影？答： 中心投影 ．

（2）请你在图中画出表示小树影长的线段 AB．

2.在同车道行驶的机动车，后车应当与前车保持足以采取紧急制动措施的安全距离．如图，在一个路口，一辆长为 10m 的大巴车遇红灯后停在距交通信号灯 20m 的停止线处，小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾 xm，若大巴车车顶高于小张的水平视线 0.8m，红灯下沿高于小张的水平视线3.2m，若小张能看到整个红灯，则 x 的最小值为 10m ．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

90 数学加分宝三.（本题满分10分）

在同一时刻两根垂直于水平地面的木竿在太阳光下的影子如图所示，其中木竿AB2.5m，它的影子BC  2m ，木竿 PQ 的影子有一部分落在了墙上(MN), PM 1.6m, MN 1m，求木竿PQ的长度．【答案】3m

【分析】过 N 点作 ND⊥PQ 于 D，根据同一时刻物高与影长成正比求出 QD 的影长，再根据此影长列出比例式求解即可．

【详解】解：如图：过 N 点作 ND⊥PQ 于 D，

∴四边形 DPMN 是矩形

∴DN=PM,PD=MN

∴

BC DN

AB QD

 ，

又∵AB=2.5，BC=2，DN=PM=1.6，NM=1，

∴QD= AB • DN

BC

= 2.5 1.6

2



=2（m），

∴PQ=QD+DP=QD+NM=2+1=3（m）．

故答案为 3m．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

91 数学加分宝9上《天天练》第10周②答案（满分30分）一.（每题5分，共10分）

1．小明的身高为 1.6m，某一时刻他在阳光下的影子长为 2m，与他邻近的一棵树的影长为10m，则这棵树的高为_____m．

【答案】8

2．如图，在 A 时测得某树的影长为 4m，B 时又测得该树的影长为 16m，若两次日照的光线互相垂直，则树的高度为______．

【答案】8m

二.（每题5分，共10分）

1.墙壁CD 上 D 处有一盏灯（如图），小明站在 A 处测得他的影长与身高相等，都为1.6 米，他向墙壁走1米到 B 处时发现影子的顶端刚好落在 A 点处，则灯泡与地面的距离CD=___ 1564_____.

2.如图，路灯距地面 8 米，身高 1.6 米的小明从点 A 处沿 AO所在的直线行走14 米到点B时，人影长度（ C ）

A.长了 3.5m B.变长了 2.5m C.变短了 3.5m D.变短了2.5m

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

92 数学加分宝三.（本题满分10分）

小明同学想利用影子测量校园内的旗杆的高度.他在某一时刻测得一棵小树高为1.5 m，其影长为1.2m，当他测量教学楼旁的旗杆影长时，因旗杆靠近教学楼，有一部分影子落在墙上，经测量，地面部分影长为6.4 m ，墙上影长为 1.4 m （如图），那么这根旗杆高约多少？

解：作 CE⊥AB 于 E，

∵DC⊥BD 于 D，AB⊥BD 于 B，

∴四边形 BDCE 为矩形，

∴CE=BD=6.4m，BE=DC=1.4m，

∵同一时刻物高与影长所组成的三角形相似，

∴ ，解得 AE=8m，

∴AB=8+1.4=9.4m．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

93 数学加分宝9上《天天练》第10周③答案（满分30分）一.（每题5分，共10分）

1．如图，一个水平放置的正六棱柱，这个正六棱柱的主视图是（ ）

A． B． C． D．

【答案】A

2．一个几何体的三视图如图所示，则该几何体的表面积为___________．（其中取3）【答案】13

二.（每题5分，共10分）

1.如图是由几块相同的小正方体搭成的立体图形的三视图，则这个立体图形中小正方体共有________个；【答案】9

2.一个几何体由若干个大小相同点小立方块搭成，如图分别是从它的正面、上面看到的形状图，该几何体至少是用__________块小立方块搭成的．

【答案】6

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

94 数学加分宝三.（本题满分10分）

如图，在路灯下，小明的身高如图中线段 AB 所示，他在地面上的影子如图中线段AC 所示，小亮的身高如图中线段 FG 所示，路灯灯泡在线段 DE 上. （1）请你确定灯泡所在的位置，并画出小亮在灯光下形成的影子. （2）如果小明的身高 AB=1.6m，他的影子长 AC=1.4m，且他到路灯的距离AD=2.1m，求灯泡的高.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

95 数学加分宝9上《天天练》第10周④答案（满分30分）一.（每题5分，共10分）

1．用小立方块搭成的几何体，从左面看和从上面看如图所示，搭成这样的几何体最多要x 个小立方块，最少要 y 个小立方块，则 x+y 等于____________．

【答案】12

2.一个由若干个小正方体组成的几何体的主视图和俯视图如图所示，则需要构成这样的几何体最多能有小正方体的个数为______________. 【答案】10

二.（每题5分，共10分）

1.一个几何体由若干个棱长为1cm的小正方体搭成，如图所示分别是从它的正面、左面、上面看到的形状图，则这个几何体的表面积是________

2 cm ．

【答案】24

2.一个由 16 个完全相同的小立方块搭成的几何体，其最下面一层摆放了 9 个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有 10 种．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

96 数学加分宝三.（本题满分10分）

如图，花丛中有一路灯杆 AB ，在灯光下，小丽在 D 点处的影长 DE  3米，沿BD方向行走到达G点，DG  5米，这时小丽的影长GH  5 米.如果小丽的身高为 1.7 米，求路灯杆AB的高度（精确到0.1米）AB=5.95≈6.0（米）

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

97 数学加分宝9上《天天练》第10周⑤答案（满分30分）一.（每题5分，共10分）

1．10 个棱长为 1cm 的正方体，摆放成如图的形状，则这个图形的表面积为________cm2

【答案】36

2．（18 年市南期末）将一个正方体木块涂成红色，然后如图把它的棱三等分，再沿等分线把正方体切开，可以得到 27 个小正方体.其中三面涂色的小正方体有 8 个，两面涂色的小正方体有12 个，一面涂色的小正方体有 6 个，各面都没有涂色的小正方体有 1 个；现将这个正方体的棱 n 等分，如果得到各面都没有涂色的小正方体 125 个，那么 n 的值为 7 .二.（每题5分，共10分）

1.（19 年市北期末）如图，是由若干个小正方体组成的立体图形，阴影部分是空缺的通道，一直通到对面，这个立体图形是由 38 个小正方体组成的.

2.（20 年西海岸二模 14）如图，棱长为 5 的正方体无论从哪一个面看，都有两个直通的边长为1的正方形孔，则这个有孔的正方体的表面积（含孔内各面）是____222______.

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

98 数学加分宝三.（本题满分10分）

学习投影后，小明、小颖利用灯光下自己的影子长度来测量一路灯的高度，并探究影子长度的变化规律．如图所示，在同一时间，身高为 1.6 m 的小明(AB)的影子 BC 长是 3m，而小颖(EH)刚好在路灯灯泡的正下方H 点，并测得 HB＝6m．

（1）请在图中画出形成影子的光线，并确定路灯灯泡所在的位置 G；

（2）求路灯灯泡的垂直高度 GH；

（3）如果小明沿线段 BH 向小颖(点 H)走去，当小明走到 BH 中点 B1处时，求其影子B1C1的长；当小明继续走剩下的路程的

1

3

到 B2处时，求其影子 B2C2的长；当小明继续走剩下路程的14到B3处时，……按此规律继续走下去，当小明走剩下路程的

1

n 1

到 Bn 处时，其影子 BnCn 的长为_____________m(直接用含n的代数式表示)．

（1）如图所示：

（2）由题意得△ABC∽△GHC，∴

AB BC

GH HC

 ，∴

1.6 3

GH6 3 



，∴ GH＝4.8m．即路灯灯泡的垂直高度为 4.8 m．

（3）∵ △A1B1C1∽△GHC1，∴

1 1 1 1

1

A B B C

GH HC

 ．

设 B1C1长为 x m，则

1.6

4.8 3

x

x 



，

解得

3

2

x  ，即 1 1

3

2

B C  m．同理

2 2

2 2

1.6

4.8 2

B C

B C





，解得 B2C2＝1m；…；由此可得当小明走剩下路程的

1

n 1到 Bn 处时，其影子的长为

3

1

BnCn n 



m．

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

99 数学加分宝9 上《天天练》第11 周①答案（满分30 分）一.（每题 5 分，共 10 分）

1.下列函数中，反比例函数是（ D ）

A. x( y 1) 1 B. 1

1





x

y C. 2

1

x

y  D. x

y 3

12.下列等式中， ① ⑦ 是一次函数；② ③ ⑤是反比例函数； ① 是正比例函数. ①

3

x

y  ②

x

y

2   ③ xy  21

④

2

5





x

y ⑤

x

y 2

3   ⑥ 3

1  

x

y

⑦ y  x  4

二.（每题 5 分，共 10 分）

1.如果函数 2 1 

m y x 为反比例函数，则 m 的值是（ B ）

A. 1 B. 0 C. 2

1

D. 1

2. 2 3

2 ( )

   

k k y k k x 是反比例函数，那么k= 2 ；

三.（每题 5 分，共 10 分）

1.若函数

2 3 ( 1) m y m x

   是反比例函数，则m的值是  2 .

2. 如果函数 2 2

2   

k k y kx 是反比例函数，那么 k =__ 2

1 1或__，此函数的解析式是xyxy211或；

李老师专用教案（精品原创） 微信：15192086110抖音：866460001

100 数学加分宝9 上《天天练》第11 周②答案（满分30 分）一.（每题 5 分，共 10 分）

1.若函数

x

m

y

 2  图象在其每个象限内，y随x的增大而增大，则m的取值范围是m＜2.

2.下列函数：①

x

y

1  ；②

x

y

0.3  ；③

x

y 2

1  ；④

x

y 1007  中，

（1）图象位于一、三象限的有 ①②③ ；

（2）在每一象限内，y随x的增大而增大的有 ④ .二.（每题 5 分，共 10 分）

1.已知函数

x

m

y  的图象如图，以下结论：

① m＜0；

②在每个分支上 y 随 x 的增大而增大；

③若点 A （－1， a ）、点 B （2，b ）在图象上，则 a＜b ；

④若点 P （ x ， y ）在图象上，则点 P1（  x ，  y ）也在图象上.其中正确的个数是（ B ）

A.4 个 B.3 个 C.2 个 D.1 个

2.若 A（－3， y1 ），B（－2， 2 y ），C（－1， 3 y ）三点都在函数

x

y

1  的图象上，则y1 ，2y，3y的大小关系是（ B ）

A. y1 ＞ 2 y ＞ 3 y B. y1 ＜ 2 y ＜ 3 y C. y1 ＝ 2 y ＝ 3 y D. y1 ＜3 y ＜2 y三.（每题 5 分，共 10 分）

1.已知点 ( )

1 1 A x，y ， ( )

2 2 B x ，y 在反比例函数

x

y

3   的图象上，若 0y1 y2 ，则下列结论正确的是（ C ）

A. 0 x1  x2  B. 0 x2  x1  C. 1 2 0  x  x D. 2 1 0xx2.（19年市南期末）反比例函数

x

y

3  图象上有是三个点（ x1 ， 1 y ）（ 2 x ， 2 y ）（3 x ，3 y），若1 23xx0x，则 1 y ， 2 y ， 3 y 的大小关系是 （ A ）

A. 2 1 3 y  y  y B. 1 2 3 y  y  y C. 3 1 2 y  y  y D. 3 2 1 y  y y